| Language Reference |
VNORMAL Call
generates a multivariate normal random series
- CALL VNORMAL( series, mu, sigma, n <, seed>);
The inputs to the VNORMAL subroutine are as follows:
- mu
- specifies a
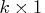 (or
(or 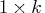 ) mean vector,
where
) mean vector,
where 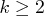 is the number of variables.
You must specify either mu or sigma.
If mu is not specified, a zero vector is used.
is the number of variables.
You must specify either mu or sigma.
If mu is not specified, a zero vector is used.
- sigma
- specifies a
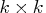 symmetric positive-definite covariance matrix.
By default, sigma is an identity matrix with dimension
symmetric positive-definite covariance matrix.
By default, sigma is an identity matrix with dimension 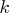 .
You must specify either mu or sigma.
If sigma is not specified, an identity matrix is used.
.
You must specify either mu or sigma.
If sigma is not specified, an identity matrix is used.
- n
- specifies the length of the series. If n is not specified,
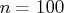 is used.
is used.
- seed
- is a scalar containing the random number seed.
At the first execution of the subroutine,
the seed variable is used as follows:
If seed > 0, the input seed is used for generating the series.
If seed = 0, the system clock is used to generate the seed.
If seed < 0, the value (-1)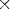 (seed) is used for generating the series.
(seed) is used for generating the series.
If the seed is not supplied, the system clock is used to generate the seed.
On subsequent calls of the subroutine in the DO loop like environment the seed variable is used as follows: If seed > 0, the seed remains unchanged. In other cases, after each execution of the subroutine, the current seed is updated internally.
The VNORMAL subroutine returns the following value:
- series
- is an
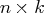 matrix that contains the generated normal random series.
matrix that contains the generated normal random series.
Consider a bivariate (
mu = { 10, 20 };
sigma= { 1.0 0.5, 0.5 1.25};
call vnormal(et, mu, sigma, 100);
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.