Language Reference: VARMALIK Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

VARMALIK Call

computes the log-likelihood function for a VARMA() model

CALL VARMALIK( lnl, series, phi, theta, sigma <, p, q, opt> );

The inputs to the VARMALIK subroutine are as follows:

series

specifies an

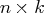matrix containing the vector time series (assuming mean zero), where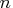

is the number of observations and 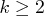$k\geq 2$ is the number of variables.

phi

specifies a

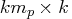matrix containing the autoregressive coefficient matrices, where

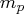is the number of the elements in the subset of the AR order. You must specify either phi or theta.

theta

specifies a

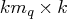matrix containing the moving-average coefficient matrices, where

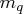is the number of the elements in the subset of the MA order. You must specify either phi or theta.

sigma

specifies a

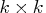covariance matrix of the innovation series. If you do not specify sigma, an identity matrix is used.

p

specifies the subset of the AR order. See the VARMACOV subroutine.

q

specifies the subset of the MA order. See the VARMACOV subroutine.

opt

specifies the method of computing the log-likelihood function:

opt=0: requests the multivariate innovations algorithm. This algorithm requires that the time series is stationary and does not contain missing observations.
opt=1: requests the conditional log-likelihood function. This algorithm requires that the number of the observations in the time series must be greater than p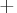q and that the series does not contain missing observations.
opt=2: requests the Kalman filtering algorithm. This is the default and is used if the required conditions in opt=0 and opt=1 are not satisfied.

The VARMALIK subroutine returns the following value:

lnl: is a 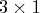matrix containing the log-likelihood function, the sum of log determinant of the innovation variance, and the weighted sum of squares of residuals. The log-likelihood function is computed as 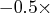(the sum of last two terms).

The options opt=0 and opt=2 are equivalent for stationary time series without missing values. Setting opt=0 is useful for a small number of the observations and a high order of p and q; opt=1 is useful for a high order of p and q; opt=2 is useful for a low order of p and q, or for missing values in the observations.

Consider the following bivariate (

) VARMA(1,1) model:

$y_t = \phi y_{t-1} + {\epsilon}_t - \theta {\epsilon}_{t-1}$

$\phi=[\matrix{1.2 & -0.5 \cr 0.6 & 0.3 \cr }] \theta=[\matrix{-0.6 & 0.3 \cr 0.3 & 0.6 \cr }] \sigma=[\matrix{1.0 & 0.5 \cr 0.5 & 1.25\cr }]$

To compute the log-likelihood function of this model, you can use the following statements:

  
   phi  = { 1.2 -0.5, 0.6 0.3 }; 
   theta= {-0.6  0.3, 0.3 0.6 }; 
   sigma= { 1.0  0.5, 0.5 1.25}; 
   call varmasim(yt, phi, theta) sigma=sigma; 
   call varmalik(lnl, yt, phi, theta, sigma);

Top of Page