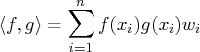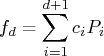Language Reference: ORPOL Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

ORPOL Function

generates orthogonal polynomials on a discrete set of points

ORPOL( x<, maxdegree<, weights>)

The inputs to the ORPOL function are as follows:

x: is an 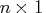vector of values on which the polynomials are to be defined.
maxdegree: specifies the maximum degree polynomial to be computed. If maxdegree is omitted, the default value is 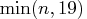$\min(n,19)$ . If weights is specified, maxdegree must also be specified.
weights: specifies an vector of nonnegative weights associated with the points in x. If you specify weights, you must also specify maxdegree. If maxdegree is not specified or is specified incorrectly, the default weights (all weights are 1) are used.

The ORPOL matrix function generates orthogonal polynomials evaluated at the

points contained in x by using the algorithm of Emerson (1968). The result is a column-orthonormal matrix

with

rows and maxdegree

columns such that $p^'{diag}({weights})p = i$ . The result of evaluating the polynomial of degree

at the

th element of x is stored in

.

The maximum number of nonzero orthogonal polynomials (

) that can be computed from the vector and the weights is the number of distinct values in the vector, ignoring any value associated with a zero weight.

The polynomial of maximum degree has degree of

. If the value of maxdegree exceeds

, then columns

,..., maxdegree

of the result are set to 0. In this case,

$p^'{diag}({weights})p = [ i(r) & 0 \ 0 & 0 \ ]$

The following statement results in a matrix with three orthogonal columns:

  
   x = T(1:5); 
   P = orpol(x,2); 
  
                                P 
  
                   0.4472136 -0.632456 0.5345225 
                   0.4472136 -0.316228 -0.267261 
                   0.4472136         0 -0.534522 
                   0.4472136 0.3162278 -0.267261 
                   0.4472136 0.6324555 0.5345225

The first column is a polynomial of degree 0 (a constant polynomial) evaluated at each point of

. The second column is a polynomial of degree 1 evaluated at each point of

. The third column is a polynomial of degree 2 evaluated at each point of

Normalization of the Polynomials

The columns of

are orthonormal with respect to the inner product

$\langle f,g \rangle = \sum_{i=1}^n f(x_i) g(x_i) w_i$

as the following code shows.

  
    start InnerProduct(f,g,w); 
       h = f#g#w; 
       return (h[+]); 
    finish; 
  
    /* Verify orthonormal */ 
    reset fuzz;         /* print tiny numbers as zero */ 
    w = j(ncol(x),1,1); /* default weight is all ones */ 
    do i = 1 to 3; 
       do j = 1 to i; 
          InnerProd = InnerProduct(P[,i], P[,j], w ); 
          print i j InnerProd; 
       end; 
    end;

Some reference books on orthogonal polynomials do not normalize the columns of the matrix that represents the orthogonal polynomials. For example, a textbook might give the following as a fourth-degree polynomial evaluated on evenly spaced data:

  
    textbookPoly = { 1 -2  2 -1  1, 
                     1 -1 -1  2 -4, 
                     1  0 -2  0  6, 
                     1  1 -1 -2 -4, 
                     1  2  2  1  1 };

To compare this representation to the normalized representation that ORPOL produces, use the following program:

  
    /* Normalize the columns of textbook representation */ 
    normalPoly = textbookPoly; 
    do i = 1 to ncol( normalPoly ); 
       v = normalPoly[,i]; 
       norm = sqrt(v[##]); 
       normalPoly[,i] = v / norm; 
    end; 
  
    /* Compare the normalized matrix with ORPOL */ 
    x = T(1:5); /* Any evenly spaced data gives the same answer */ 
    imlPoly = orpol( x, 4 ); 
  
    diff = imlPoly - normalPoly; 
    maxDiff = abs(diff)[<>]; 
    reset fuzz; /* print tiny numbers as zero */ 
    print maxDiff; 
  
  
             MAXDIFF 
  
                0

Polynomial Regression

A typical use for orthogonal polynomials is to fit a polynomial to a set of data. Given a set of points

, the classical theory of orthogonal polynomials says that the best approximating polynomial of degree

is given by

$f_d = \sum_{i=1}^{d+1} c_i p_i$

where $c_i = \langle y,p_i \rangle / \langle p_i,p_i \rangle$ and where

is the

th column of the matrix

returned by ORPOL. But the matrix is orthonormal with respect to the inner product, so $\langle p_i,p_i\rangle = 1$ for all

. Thus you can easily compute a regression onto the span of polynomials.

In the following program, the weight vector is used to overweight or underweight particular data points. The researcher has reasons to doubt the accuracy of the first measurement. The last data point is also underweighted because it is a leverage point and is believed to be an outlier. The second data point was measured twice and is overweighted. (Rerunning the program with a weight vector of all ones, and examining the new values of the fit variable is a good way to understand the effect of the weight vector.)

  
    x = {0.1, 2,   3,  5,    8,   10, 20}; 
    y = {0.5, 1, 0.1, -1, -0.5, -0.8, 0.1}; 
  
    /* The second measurement was taken twice. 
       The first and last data points are underweighted 
       because of uncertainty in the measurements.  */ 
    w = {0.5, 2,   1,  1,    1,    1, 0.2}; 
    maxDegree = 4; 
    P = orpol(x,maxDegree,w); 
  
    /* The best fit by a polynomial of degree k is 
       Sum c_i P_i  where c_i = <f,P_i> */ 
    c = j(1,maxDegree+1); 
    do i = 1 to maxDegree+1; 
       c[i] = InnerProduct(y,P[,i],w); 
    end; 
  
    FitResults = j(maxDegree+1,2); 
    do k = 1 to maxDegree+1; 
       fit = P[,1:k] * c[1:k]; 
       resid = y - fit; 
       FitResults[k,1] = k-1;       /* degree of polynomial */ 
       FitResults[k,2] = resid[##]; /* sum of square errors */ 
    end; 
    print FitResults[colname={"Degree" "SSE"}];

The results of this program are as follows:

  
      FITRESULTS 
    Degree       SSE 
  
         0 3.1733014 
         1 4.6716722 
         2 1.3345326 
         3 1.3758639 
         4 0.8644558

Testing Linear Hypotheses

ORPOL can also be used to test linear hypotheses. Suppose you have an experimental design with

factor levels. (The factor levels can be equally or unequally spaced.) At the

th level, you record

observation,

. If

, then the design is said to be balanced, otherwise it is unbalanced. You want to fit a polynomial model to the data and then ask how much variation in the data is explained by the linear component, how much variation is explained by the quadratic component after the linear component is taken into account, and so on for the cubic, quartic, and higher-level components.

To be completely concrete, suppose you have four factor levels (1, 4, 6, and 10) and that you record seven measurements at first level, two measurements at the second level, three measurements at the third level, and four measurements at the fourth level. This is an example of an unbalanced and unequally spaced factor-level design. The following program uses orthogonal polynomials to compute the Type I sum of squares for the linear hypothesis. (The program works equally well for balanced designs and for equally spaced factor levels.)

The program calls ORPOL to generate the orthogonal polynomial matrix

, and uses it to form the Type I hypothesis matrix

. The program then uses the DESIGN function to generate

, the design matrix associated with the experiment. The program then computes

, the estimated parameters of the linear model.

Since

was expressed in terms of the orthogonal polynomial matrix

, the computations involved in forming the Type I sum of squares are considerably simplified.

Here is the code:

  
    /* unequally spaced and unbalanced factor levels */ 
    levels = { 
    1,1,1,1,1,1,1, 
    4,4, 
    6,6,6, 
    10,10,10,10}; 
  
    /* data for y. Make sure the data are sorted 
       according to the factor levels */ 
    y = { 
    2.804823, 0.920085, 1.396577, -0.083318, 
    3.238294, 0.375768, 1.513658,            /* level 1 */ 
    3.913391, 3.405821,                      /* level 4 */ 
    6.031891, 5.262201,  5.749861,           /* level 6 */ 
    10.685005, 9.195842, 9.255719,  9.204497 /* level 10 */ 
    }; 
  
    a      = {1,4,6,10}; /* spacing */ 
    trials = {7,2,3,4};  /* sample sizes */ 
    maxDegree = 3; /* model with Intercept,a,a##2,a##3 */ 
  
    P = orpol(a,maxDegree,trials); 
  
    /* Test linear hypotheses: 
       How much variation is explained by the 
       i_th polynomial component after components 
       0..(i-1) have been taken into account? */ 
  
    /* the columns of L are the coefficients of the 
       orthogonal polynomial contrasts */ 
    L = diag(trials)*P; 
  
    /* form design matrix */ 
    x = design(levels); 
  
    /* compute b, the estimated parameters of the 
       linear model. b is the mean of the y values 
       at each level. 
       b = ginv(x'*x) * x` * y 
       but since x is the output from DESIGN, then 
       x`*x = diag(trials) and so 
       ginv(x`*x) = diag(1/trials) */ 
    b = diag(1/trials)*x`*y; 
  
    /* (L`*b)[i] is the best linear unbiased estimated 
       (BLUE) of the corresponding orthogonal polynomial 
       contrast */ 
    blue = L`*b; 
  
    /* the variance of (L`*b) is 
       var(L`*b) = L`*ginv(x`*x)*L 
         =[P`*diag(trials)]*diag(1/trials)*[diag(trials)*P] 
         = P`*diag(trials)*P 
         = Identity         (by definition of P) 
  
       so therefore the standardized square of 
       (L`*b) is computed as 
       SS1[i] = (blue[i]*blue[i])/var(L`*b)[i,i]) 
              = (blue[i])##2                            */ 
  
    SS1 = blue # blue; 
    rowNames = {'Intercept' 'Linear' 'Quadratic' 'Cubic'}; 
    print SS1[rowname=rowNames format=11.7 label="Type I SS"];

The resulting output is as follows:

  
  
          Type I SS 
  
    Intercept 331.8783538 
    Linear    173.4756050 
    Quadratic   0.4612604 
    Cubic       0.0752106

This indicates that most of the variation in the data can be explained by a first-degree polynomial.

Generating Families of Orthogonal Polynomials

There are classical families of orthogonal polynomials (for example, Legendre, Laguerre, Hermite, and Chebyshev) that arise in the study of differential equations and mathematical physics. These "named" families are orthogonal on particular intervals

with respect to the inner product $\int_b^a f(x)g(x)w(x)\, dx$ . The functions returned by ORPOL are different from these named families because ORPOL uses a different inner product. There are no IML functions that can automatically generate these families; however, you can write an IML program to generate them.

Each named polynomial family $\{p_j\}$ , $j\geq 0$ satisfies a three-term recurrence relation of the form

$p_j = (a_j + x b_j)p_{j-1} - c_j p_{j-2}$

where the constants

, and

are relatively simple functions of

. To generate these "named" families, use the three-term recurrence relation for the family. The recurrence relations are found in references such as Abramowitz and Stegun (1972) or Thisted (1988).

For example, the so-called Legendre polynomials (represented

for the polynomial of degree

) are defined on

with the weight function

. They are standardized by requiring that

for all $j\geq 0$ . Thus

. The linear polynomial

is orthogonal to

so that

$\int_{-1}^1 p_1(x) p_0(x)\, dx = \int_{-1}^1 a + bx\, dx = 0$

which implies

. The standardization

implies that

. The remaining Legendre polynomials can be computed by looking up the three-term recurrence relation:

, and

. The following program computes Legendre polynomials evaluated at a set of points.

  
 maxDegree = 6; 
  
 /* evaluate polynomials at these points */ 
 x = T( do(-1,1,0.05) ); 
  
 /* define the standard Legendre Polynomials 
    Using the 3-term recurrence with 
    A[j]=0, B[j]=(2j-1)/j, and C[j]=(j-1)/j 
    and the standardization P_j(1)=1 
    which implies P_0(x)=1, P_1(x)=x. */ 
 legendre = j(nrow(x), maxDegree+1); 
 legendre[,1] = 1; /* P_0 */ 
 legendre[,2] = x; /* P_1 */ 
  
 do j = 2 to maxDegree; 
    legendre[,j+1] = (2*j-1)/j # x # legendre[,j] - 
                       (j-1)/j # legendre[,j-1]; 
 end;

Top of Page