Language Reference

OPSCAL Function

rescales qualitative data to be a least squares fit to qualitative data

OPSCAL( mlevel, quanti<, qualit>)

The inputs to the OPSCAL function are as follows:

mlevel

specifies a scalar that has one of two values. When mlevel is 1 the qualit matrix is at the nominal measurement level; when mlevel is 2 it is at the ordinal measurement level.

quanti

specifies an 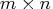matrix of quantitative information assumed to be at the interval level of measurement.

qualit

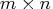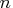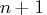specifies an matrix of qualitative information whose level of measurement is specified by mlevel. When qualit is omitted, mlevel must be 2. When omitted, a temporary qualit is constructed that contains the integers from 1 to in the first row, from to 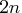in the second row, from 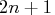to 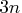in the third row, and so forth, up to the integers 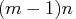to 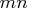in the last(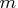th) row. Note that you cannot specify qualit as a character matrix.

The result of the OPSCAL function is the optimal scaling transformation of the qualitative (nominal or ordinal) data in qualit. The optimal scaling transformation result

• is a least squares fit to the quantitative data in quanti
• preserves the qualitative measurement level of qualit

When qualit is at the nominal level of measurement, the optimal scaling transformation result is a least squares fit to quanti, given the restriction that the category structure of qualit must be preserved. If element of qualit is in category , then element of the optimum scaling transformation result is the mean of all those elements of quanti that correspond to elements of qualit that are in category .

For example, consider these statements:

  
    quanti={5  4  6  7  4  6  2  4  8  6}; 
    qualit={6  6  2 12  4 10  4 10  8  6}; 
    os=opscal(1,quanti,qualit);
 

The resulting vector has the following values:

  
            OS        1 row     10 cols    (numeric) 
  
           5      5     6       7       3       5       3 
 :         5      8      5
 

The optimal scaling transformation result is said to preserve the nominal measurement level of qualit because wherever there was a qualit category , there is now a result category label . The transformation is least squares because the result element is the mean of appropriate elements of quanti. This is Young's (1981) discrete-nominal transformation.

When qualit is at the ordinal level of measurement, the optimal scaling transformation result is a least squares fit to quanti, given the restriction that the ordinal structure of qualit must be preserved. This is done by determining blocks of elements of qualit so that if element of qualit is in block , then element of the result is the mean of all those quanti elements corresponding to block elements of qualit so that the means are (weakly) in the same order as the elements of qualit. For example, consider these statements:

  
    quanti={5  4  6  7  4  6  2  4  8  6}; 
    qualit={6  6  2 12  4 10  4 10  8  6}; 
    os=opscal(2,quanti,qualit);
 

The resulting vector has the following values:

  
              OS      1 row    10 cols  (numeric) 
  
         5        5      4      7     4     6     4 
    :    6        6      5
 

This transformation preserves the ordinal measurement level of qualit because the elements of qualit and the result are (weakly) in the same order. It is least squares because the result elements are the means of appropriate elements of quanti. By comparing this result to the nominal one, you see that categories whose means are incorrectly ordered have been merged together to form correctly ordered blocks. This is known as Kruskal's (1964) least squares monotonic transformation. Consider the following statements:

  
    quanti={5  3  6  7  5  7  8  6  7  8}; 
    os=opscal(2,quanti);
 

These statements imply that

  
    qualit={ 1  2  3  4  5  6  7  8  9 10} ;
 

This means that the resulting vector has the following values:

  
            OS       1 row   10 cols    (numeric) 
  
         4     4      6       6        6      7      7 
    :    7     7      8