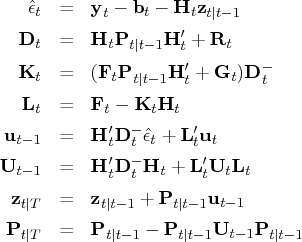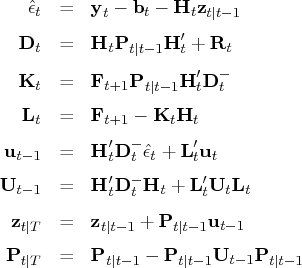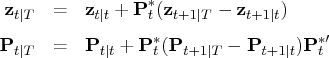| Language Reference |
KALCVS Call
uses backward recursions to compute the smoothed
estimate ![]() and its covariance matrix,
and its covariance matrix, ![]() ,
where
,
where ![]() is the number of observations in the complete data set
is the number of observations in the complete data set
- CALL KALCVS( sm, vsm, data,
 ,
, 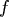 ,
, 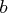 ,
, 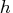 ,
var, pred, vpred <,un, vun>);
,
var, pred, vpred <,un, vun>);
The inputs to the KALCVS subroutine are as follows.
- data
- is a
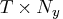 matrix containing
data
matrix containing
data 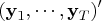 .
. 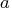
- is an
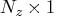 vector for a time-invariant input
vector in the transition equation, or a
vector for a time-invariant input
vector in the transition equation, or a 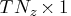 vector containing input vectors in the transition equation.
vector containing input vectors in the transition equation.
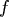
- is an
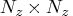 matrix for a time-invariant
transition matrix in the transition equation, or a
matrix for a time-invariant
transition matrix in the transition equation, or a
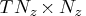 matrix containing
matrix containing 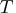 transition matrices.
transition matrices.
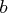
- is an
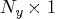 vector for a time-invariant input vector
in the measurement equation, or a
vector for a time-invariant input vector
in the measurement equation, or a 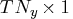 vector
containing input vectors in the measurement equation.
vector
containing input vectors in the measurement equation.
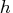
- is an
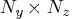 matrix for a time-invariant
measurement matrix in the measurement equation, or
a
matrix for a time-invariant
measurement matrix in the measurement equation, or
a 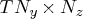 matrix containing
matrix containing 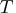 time-variant
time-variant
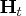 matrices in the measurement equation.
matrices in the measurement equation.
- var
- is an
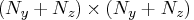 covariance matrix
for the errors in the transition and the measurement
equations, or a
covariance matrix
for the errors in the transition and the measurement
equations, or a 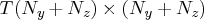 matrix containing covariance matrices in the transition
equation and measurement equation noises - that is,
matrix containing covariance matrices in the transition
equation and measurement equation noises - that is,
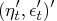 .
. - pred
- is a
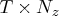 matrix containing one-step
forecasts
matrix containing one-step
forecasts 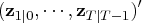 .
. - vpred
- is a
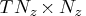 matrix containing mean
square error matrices of predicted state vectors
matrix containing mean
square error matrices of predicted state vectors
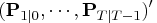 .
. - un
- is an optional
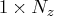 vector containing
vector containing 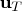 .
The returned value is
.
The returned value is 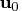 .
. - vun
- is an optional
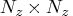 matrix containing
matrix containing 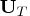 .
The returned value is
.
The returned value is 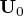 .
.
- sm
- is a
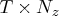 matrix containing smoothed state
vectors
matrix containing smoothed state
vectors 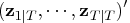 .
. - vsm
- is a
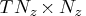 matrix containing covariance matrices of
smoothed state vectors
matrix containing covariance matrices of
smoothed state vectors 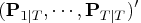 .
.
The smoothing algorithm uses one-step forecasts and their covariance matrices, which are given in the KALCVF call. For notation,
When the SSM is specified by using the alternative transition equation
You can use the KALCVS call regardless of the specification of the transition equation when
The KALCVS call is accompanied by the KALCVF call, as shown in the following code. Note that you do not need to specify UN and VUN.
call kalcvf(pred,vpred,filt,vfilt,y,0,a,f,b,h,var);
call kalcvs(sm,vsm,y,a,f,b,h,var,pred,vpred);
You can also compute the smoothed estimate and its
covariance matrix on an observation-by-observation basis.
When the SSM is time invariant, the
following example performs smoothing.
In this situation, you should initialize
UN and VUN as matrices of value 0, as in the following code:
call kalcvf(pred,vpred,filt,vfilt,y,0,a,f,b,h,var); n = nrow(y); nz = ncol(f); un = j(1,nz,0); vun = j(nz,nz,0); do i = 1 to n; y_i = y[n-i+1,]; pred_i = pred[n-i+1,]; vpred_i = vpred[(n-i)*nz+1:(n-i+1)*nz,]; call kalcvs(sm_i,vsm_i,y_i,a,f,b,h,var,pred_i,vpred_i,un,vun); sm = sm_i // sm; vsm = vsm_i // vsm; end;
The KALCVF call has an example program that includes the KALCVS call.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.