| Graphics Examples |
Example 12.1: Scatter Plot Matrix
With the viewport capability of the IML graphics subroutine, you can arrange several graphs on a page. In this example, multiple graphs are generated from three variables and are displayed in a scatterplot matrix. For each variable, one contour plot is generated with each of the other variables as the dependent variable. For the graphs on the main diagonal, a box-and-whiskers plot is generated for each variable.
This example takes advantage of user-defined IML modules:
- BOXWHSKR
- computes median and quartiles.
- GBXWHSKR
- draws box-and-whiskers plots.
- CONTOUR
- generates confidence ellipses assuming bivariate normal data.
- GCONTOUR
- draws the confidence ellipses for each pair of variables.
- GSCATMAT
- produces the
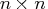 scatter plot matrix,
where
scatter plot matrix,
where 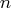 is the number of variables.
is the number of variables.
The code for the five modules and a sample data set follow. The modules produce Figure 12.9 and Figure 12.10.
/* This program generates a data set and uses iml graphics */
/* subsystem to draw a scatterplot matrix. */
/* */
data factory;
input recno prod temp a defect mon;
datalines;
1 1.82675 71.124 1.12404 1.79845 2
2 1.67179 70.9245 0.924523 1.05246 3
3 2.22397 71.507 1.50696 2.36035 4
4 2.39049 74.8912 4.89122 1.93917 5
5 2.45503 73.5338 3.53382 2.0664 6
6 1.68758 71.6764 1.67642 1.90495 7
7 1.98233 72.4222 2.42221 1.65469 8
8 1.17144 74.0884 4.08839 1.91366 9
9 1.32697 71.7609 1.76087 1.21824 10
10 1.86376 70.3978 0.397753 1.21775 11
11 1.25541 74.888 4.88795 1.87875 12
12 1.17617 73.3528 3.35277 1.15393 1
13 2.38103 77.1762 7.17619 2.26703 2
14 1.13669 73.0157 3.01566 1 3
15 1.01569 70.4645 0.464485 1 4
16 2.36641 74.1699 4.16991 1.73009 5
17 2.27131 73.1005 3.10048 1.79657 6
18 1.80597 72.6299 2.62986 1.8497 7
19 2.41142 81.1973 11.1973 2.137 8
20 1.69218 71.4521 1.45212 1.47894 9
21 1.95271 74.8427 4.8427 1.93493 10
22 1.28452 76.7901 6.79008 2.09208 11
23 1.51663 83.4782 13.4782 1.81162 12
24 1.34177 73.4237 3.42369 1.57054 1
25 1.4309 70.7504 0.750369 1.22444 2
26 1.84851 72.9226 2.92256 2.04468 3
27 2.08114 78.4248 8.42476 1.78175 4
28 1.99175 71.0635 1.06346 1.25951 5
29 2.01235 72.2634 2.2634 1.36943 6
30 2.38742 74.2037 4.20372 1.82846 7
31 1.28055 71.2495 1.24953 1.8286 8
32 2.05698 76.0557 6.05571 2.03548 9
33 1.05429 77.721 7.72096 1.57831 10
34 2.15398 70.8861 0.886068 2.1353 11
35 2.46624 70.9682 0.968163 2.26856 12
36 1.4406 73.5243 3.52429 1.72608 1
37 1.71475 71.527 1.52703 1.72932 2
38 1.51423 78.5824 8.5824 1.97685 3
39 2.41538 73.7909 3.79093 2.07129 4
40 2.28402 71.131 1.13101 2.25293 5
41 1.70251 72.3616 2.36156 2.04926 6
42 1.19747 72.3894 2.3894 1 7
43 1.08089 71.1729 1.17288 1 8
44 2.21695 72.5905 2.59049 1.50915 9
45 1.52717 71.1402 1.14023 1.88717 10
46 1.5463 74.6696 4.66958 1.25725 11
47 2.34151 90 20 3.57864 12
48 1.10737 71.1989 1.19893 1.62447 1
49 2.2491 76.6415 6.64147 2.50868 2
50 1.76659 71.7038 1.70377 1.231 3
51 1.25174 76.9657 6.96572 1.99521 4
52 1.81153 73.0722 3.07225 2.15915 5
53 1.72942 71.9639 1.96392 1.86142 6
54 2.17748 78.1207 8.12068 2.54388 7
55 1.29186 77.0589 7.05886 1.82777 8
56 1.92399 72.6126 2.61256 1.32816 9
57 1.38008 70.8872 0.887228 1.37826 10
58 1.96143 73.8529 3.85289 1.87809 11
59 1.61795 74.6957 4.69565 1.65806 12
60 2.02756 75.7877 5.78773 1.72684 1
61 2.41378 75.9826 5.98255 2.76309 2
62 1.41413 71.3419 1.34194 1.75285 3
63 2.31185 72.5469 2.54685 2.27947 4
64 1.94336 71.5592 1.55922 1.96157 5
65 2.094 74.7338 4.73385 2.07885 6
66 1.19458 72.233 2.23301 1 7
67 2.13118 79.1225 9.1225 1.84193 8
68 1.48076 87.0511 17.0511 2.94927 9
69 1.98502 79.0913 9.09131 2.47104 10
70 2.25937 73.8232 3.82322 2.49798 12
71 1.18744 70.6821 0.682067 1.2848 1
72 1.20189 70.7053 0.705311 1.33293 2
73 1.69115 73.9781 3.9781 1.87517 3
74 1.0556 73.2146 3.21459 1 4
75 1.59936 71.4165 1.41653 1.29695 5
76 1.66044 70.7151 0.715145 1.22362 6
77 1.79167 74.8072 4.80722 1.86081 7
78 2.30484 71.5028 1.50285 1.60626 8
79 2.49073 71.5908 1.59084 1.80815 9
80 1.32729 70.9077 0.907698 1.12889 10
81 2.48874 83.0079 13.0079 2.59237 11
82 2.46786 84.1806 14.1806 3.35518 12
83 2.12407 73.5826 3.58261 1.98482 1
84 2.46982 76.6556 6.65559 2.48936 2
85 1.00777 70.2504 0.250364 1 3
86 1.93118 73.9276 3.92763 1.84407 4
87 1.00017 72.6359 2.63594 1.3882 5
88 1.90622 71.047 1.047 1.7595 6
89 2.43744 72.321 2.32097 1.67244 7
90 1.25712 90 20 2.63949 8
91 1.10811 71.8299 1.82987 1 9
92 2.25545 71.8849 1.8849 1.94247 10
93 2.47971 73.4697 3.4697 1.87842 11
94 1.93378 74.2952 4.2952 1.52478 12
95 2.17525 73.0547 3.05466 2.23563 1
96 2.18723 70.8299 0.829929 1.75177 2
97 1.69984 72.0026 2.00263 1.45564 3
98 1.12504 70.4229 0.422904 1.06042 4
99 2.41723 73.7324 3.73238 2.18307 5
;
proc iml;
/*-- Load graphics --*/
call gstart;
/*--------------------*/
/*-- Define modules --*/
/*--------------------*/
/* Module : compute contours */
start contour(c,x,y,npoints,pvalues);
/* This routine computes contours for a scatter plot */
/* c returns the contours as consecutive pairs of columns */
/* x and y are the x and y coordinates of the points */
/* npoints is the number of points in a contour */
/* pvalues is a column vector of contour probabilities */
/* the number of contours is controlled by the ncol(pvalue) */
xx=x||y;
n=nrow(x);
/* Correct for the mean */
mean=xx[+,]/n;
xx=xx-mean@j(n,1,1);
/* Find principal axes of ellipses */
xx=xx` *xx/n;
call eigen(v,e,xx);
/* Set contour levels */
c=-2*log(1-pvalues);
a=sqrt(c*v[1]); b=sqrt(c*v[2]);
/* Parameterize the ellipse by angle */
t=((1:npoints)-{1})#atan(1)#8/(npoints-1);
s=sin(t);
t=cos(t);
s=s` *a;
t=t` *b;
/* Form contour points */
s=((e*(shape(s,1)//shape(t,1)))+mean`@j(1,npoints*ncol(c),1))`;
c=shape(s,npoints);
/* Returned as ncol pairs of columns for contours */
finish contour;
/*-- Module : draw contour curves --*/
start gcontour(t1, t2);
run contour(t12, t1, t2, 30, {.5 .8 .9});
window=(min(t12[,{1 3}],t1)||min(t12[,{2 4}],t2))//
(max(t12[,{1 3}],t1)||max(t12[,{2 4}],t2));
call gwindow(window);
call gdraw(t12[,1],t12[,2],,'blue');
call gdraw(t12[,3],t12[,4],,'blue');
call gdraw(t12[,5],t12[,6],,'blue');
call gpoint(t1,t2,,'red');
finish gcontour;
/*-- Module : find median, quartiles for box and whisker plot --*/
start boxwhskr(x, u, q2, m, q1, l);
rx=rank(x);
s=x;
s[rx,]=x;
n=nrow(x);
/*-- Median --*/
m=floor(((n+1)/2)||((n+2)/2));
m=(s[m,])[+,]/2;
/*-- Compute quartiles --*/
q1=floor(((n+3)/4)||((n+6)/4));
q1=(s[q1,])[+,]/2;
q2=ceil(((3*n+1)/4)||((3*n-2)/4));
q2=(s[q2,])[+,]/2;
h=1.5*(q2-q1); /*-- step=1.5*(interquartile range) --*/
u=q2+h;
l=q1-h;
u=(u>s)[+,]; /*-- adjacent values -----------------*/
u=s[u,];
l=(l>s)[+,];
l=s[l+1,];
finish boxwhskr;
/*-- Box and Whisker plot --*/
start gbxwhskr(t, ht);
run boxwhskr(t, up, q2,med, q1, lo);
/*---Adjust screen viewport and data window */
y=min(t)//max(t);
call gwindow({0, 100} || y);
mid = 50;
wlen = 20;
/*-- Add whiskers */
wstart=mid-(wlen/2);
from=(wstart||up)//(wstart||lo);
to=((wstart//wstart)+wlen)||from[,2];
/*-- Add box */
len=50;
wstart=mid-(len/2);
wstop=wstart+len;
from=from//(wstart||q2)//(wstart||q1)//
(wstart||q2)//(wstop||q2);
to=to//(wstop||q2)//(wstop||q1)//
(wstart||q1)//(wstop||q1);
/*---Add median line */
from=from//(wstart||med);
to=to//(wstop||med);
/*---Attach whiskers to box */
from=from//(mid||up)//(mid||lo);
to=to//(mid||q2)//(mid||q1);
/*-- Draw box and whiskers */
call gdrawl(from, to,,'red');
/*---Add minimum and maximum data points */
call gpoint(mid, y ,3,'red');
/*---Label min, max, and mean */
y=med//y;
s={'med' 'min' 'max'};
call gset("font","swiss");
call gset('height',13);
call gscript(wstop+ht, y, char(y,5,2),,,,,'blue');
call gstrlen(len, s);
call gscript(wstart-len-ht,y,s,,,,,'blue');
call gset('height');
finish gbxwhskr;
/*-- Module : do scatter plot matrix --*/
start gscatmat(data, vname);
call gopen('scatter');
nv=ncol(vname);
if (nv=1) then nv=nrow(vname);
cellwid=int(90/nv);
dist=0.1*cellwid;
width=cellwid-2*dist;
xstart=int((90 -cellwid * nv)/2) + 5;
xgrid=((0:nv)#cellwid + xstart)`;
/*-- Delineate cells --*/
cell1=xgrid;
cell1=cell1||(cell1[nv+1]//cell1[nv+1-(0:nv-1)]);
cell2=j(nv+1, 1, xstart);
cell2=cell1[,1]||cell2;
call gdrawl(cell1, cell2);
call gdrawl(cell1[,{2 1}], cell2[,{2 1}]);
xstart = xstart + dist; ystart = xgrid[nv] + dist;
/*-- Label variables ---*/
call gset("height", 5);
call gset("font","swiss");
call gstrlen(len, vname);
where=xgrid[1:nv] + (cellwid-len)/2;
call gscript(where, 0, vname) ;
len=len[nv-(0:nv-1)];
where=xgrid[1:nv] + (cellwid-len)/2;
call gscript(4,where, vname[nv - (0:nv-1)],90);
/*-- First viewport --*/
vp=(xstart || ystart)//((xstart || ystart) + width) ;
/* Since the characters are scaled to the viewport */
/* (which is inversely porportional to the */
/* number of variables), */
/* enlarge it proportional to the number of variables */
ht=2*nv;
call gset("height", ht);
do i=1 to nv;
do j=1 to i;
call gportstk(vp);
if (i=j) then run gbxwhskr(data[,i], ht);
else run gcontour(data[,j], data[,i]);
/*-- onto the next viewport --*/
vp[,1] = vp[,1] + cellwid;
call gportpop;
end;
vp=(xstart // xstart + width) || (vp[,2] - cellwid);
end;
call gshow;
finish gscatmat;
/*-- Placement of text is based on the character height. */
/* The IML modules defined here assume percent as the unit of */
/* character height for device independent control. */
goptions gunit=pct;
use factory;
vname={prod, temp, defect};
read all var vname into xyz;
run gscatmat(xyz, vname[1:2]); /*-- 2 x 2 scatter plot matrix --*/
run gscatmat(xyz, vname); /*-- 3 x 3 scatter plot matrix --*/
quit;
goptions gunit=cell; /*-- reset back to default --*/
|
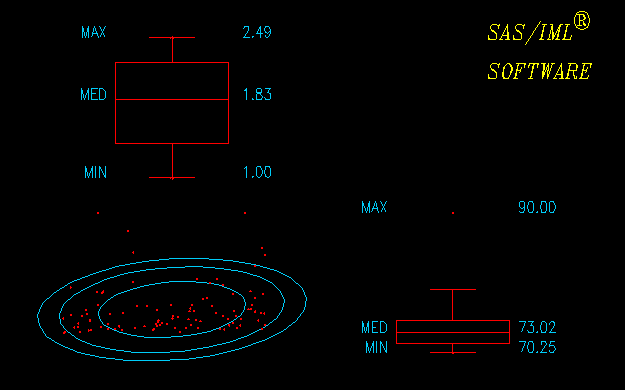
Figure 12.9: ![]() Scatter Plot Matrix
Scatter Plot Matrix
|
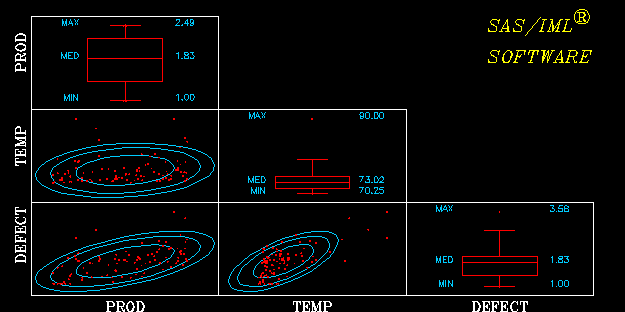
Figure 12.10: ![]() Scatter Plot Matrix
Scatter Plot Matrix
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.