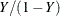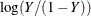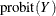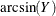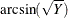Variable Transformations

Transformations for Proportion Variables

Subsections:

Figure 32.14 shows the transformations that are available when you select For proportions from the Family list. These transformations are intended for variables that represent proportions. That is, the Y variable must take values between 0 and 1. You can also use these transformations for percentages if you first divide the percentages by 100.

Chapter 7 of Atkinson (1985) is devoted to transformations of proportions. Equations for these transformations are given in Table 32.4.

Figure 32.14: Transformations for Proportions

Transformations for Proportions


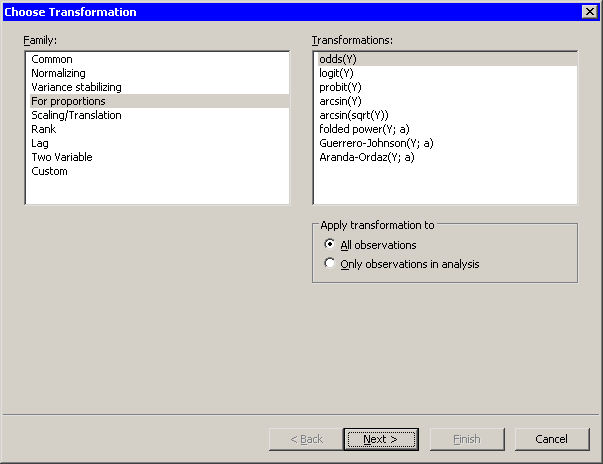
Table 32.4: Description of Transformations for Proportions 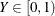$Y\in [0,1)$

 

Default

Name of

 

Transformation

Parameter

New Variable

Equation

odds(Y)

 

Odds_Y

$Y/(1-Y)$

logit(Y)

 

Logit_Y

$\log (Y/(1-Y))$

probit(Y)

 

Probit_Y

$\mbox{probit}(Y)$

arcsin(Y)

 

Arcsin_Y

$\arcsin (Y)$

arcsin(sqrt(Y))

 

Angular_Y

$\arcsin (\sqrt {Y})$

folded power(Y;a)

MLE

FPow_Y

See text.

Guerrero-Johnson(Y;a)

MLE

GJ_Y

See text.

Aranda-Ordaz(Y;a)

MLE

AO_Y

See text.


The probit function is the quantile function of the standard normal distribution.

The last three transformations in the list are similar to the Box-Cox transformation described in the section Normalizing Transformations. The parameter for each transformation is in the unit interval: $a\in [0,1]$. Typically, you choose a parameter that maximizes (or nearly maximizes) a log-likelihood function.

The log-likelihood function is defined as follows. Let N be the number of nonmissing values, and let 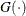$G(\cdot )$ be the geometric mean function. Each transformation has a corresponding normalized transformation 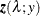$\bm {z}(\lambda ; y)$, to be defined later. Define

\[ R(\lambda ;\bm {z}) = \bm {z}’\bm {z} - \left(\Sigma z_ i \right)^2 / N \]

and define the log-likelihood function as

\[ L(\lambda ;\bm {z}) = -(N/2) \log (R(\lambda ;\bm {z})/(N-1)) \]

The following sections define the normalized transformation for the folded power, Guerrero-Johnson, and Aranda-Ordaz transformations. In each section, 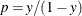$p=y/(1-y)$.