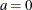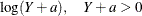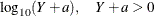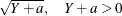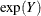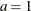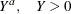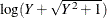Variable Transformations

Normalizing Transformations

Figure 32.12 shows the transformations that are available when you select Normalizing from the Family list. These transformations are often used to improve the normality of a variable. Equations for these transformations are given in Table 32.2.

Figure 32.12: Normalizing Transformations

Normalizing Transformations


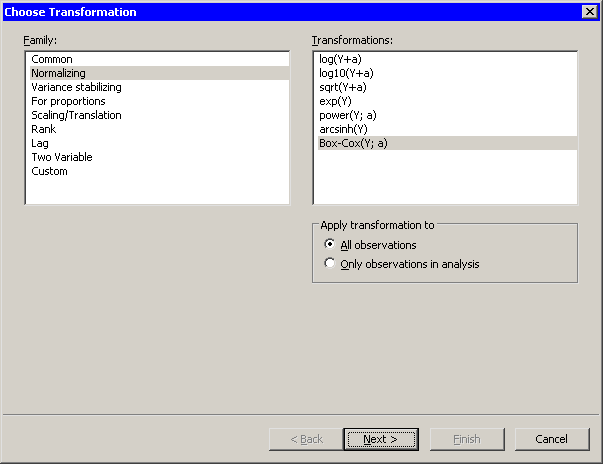
Table 32.2: Description of Normalizing Transformations

 

Default

Name of

 

Transformation

Parameter

New Variable

Equation

log(Y+a)

$a=0$

Log_Y

$\log (Y+a), \quad Y+a>0$

log10(Y+a)

$a=0$

Log10_Y

$\log _{10}(Y+a), \quad Y+a>0$

sqrt(Y+a)

$a=0$

Sqrt_Y

$\sqrt {Y+a}, \quad Y+a>0$

exp(Y)

 

Exp_Y

$\exp (Y)$

power(Y;a)

$a=1$

Pow_Y

$ Y^ a, \quad Y>0$ if a is not integral

arcsinh(Y)

 

Arcsinh_Y

$\log (Y+\sqrt {Y^2+1})$

Box-Cox(Y;a)

MLE

BC_Y

See text.


The Box-Cox transformation (Box and Cox 1964) is a one-parameter family of power transformations that includes the logarithmic transformation as a limiting case. For $Y>0$,

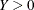\[ \mbox{BC}(y;\lambda ) = \left\{ \begin{array}{l l} \frac{y^\lambda - 1}{\lambda } & \mbox{if } \lambda \neq 0 \\ \log y & \mbox{if } \lambda = 0 \end{array} \right. \]

You can specify the parameter, 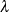$\lambda $, for the Box-Cox transformation, but typically you choose a value for 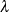$\lambda $ that maximizes (or nearly maximizes) a log-likelihood function.

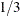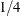SAS/IML Studio plots the log-likelihood function versus the parameter, as shown in Figure 32.8. An inset gives the lower and upper 95% confidence limits for the maximum log-likelihood estimate, the MLE estimate, and a convenient estimate. A convenient estimate is a fraction with a small denominator (such as an integer, a half integer, or an integer multiple of $1/3$ or $1/4$) that is within the 95% confidence limits about the MLE. Although the value of the parameter is not bounded, SAS/IML Studio graphs the log-likelihood function restricted to the interval $[-2,2]$.

A dialog box (see Figure 32.9) also appears that prompts you to enter the parameter value to use for the Box-Cox transformation.

The log-likelihood function for the Box-Cox transformation is defined as follows. Write the normalized Box-Cox transformation, $\bm {z}$, as

\[ \bm {z}(\lambda ; y) = \left\{ \begin{array}{l l} \frac{y^\lambda - 1}{\lambda \dot{y}^{\lambda -1}} & \mbox{if } \lambda \neq 0 \\ \dot{y} \log y & \mbox{if } \lambda = 0 \end{array} \right. \]

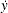where $\dot{y}$ is the geometric mean of y. Let N be the number of nonmissing values, and define

\[ R(\lambda ;\bm {z}) = \bm {z}’\bm {z} - \left(\Sigma z_ i \right)^2 / N \]

The log-likelihood function is (Atkinson 1985, p. 87)

\[ L(\lambda ;\bm {z}) = -(N/2) \log (R(\lambda ;\bm {z})/(N-1)) \]