Variable Transformations

The Folded Power Transformation

The folded power transformation is defined as

\[ \mbox{f}(y;\lambda ) = \left\{ \begin{array}{l l} \frac{y^\lambda - (1-y)^\lambda }{\lambda } & \mbox{if } \lambda \neq 0 \\ \log (p) & \mbox{if } \lambda = 0 \end{array} \right. \]

The normalized folded power transformation is defined as (Atkinson 1985, p. 139)

\[ \bm {z}_{\scriptscriptstyle f}(\lambda ; y) = \left\{ \begin{array}{l l} \frac{y^{\lambda } - (1-y)^{\lambda }}{\lambda G_{\scriptscriptstyle f}(\lambda )} & \mbox{if } \lambda \neq 0 \\ \log (p) G(y(1-y)) & \mbox{if } \lambda = 0 \end{array} \right. \]

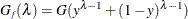where $G_{\scriptscriptstyle f}(\lambda )= G(y^{\lambda -1} +(1-y)^{\lambda -1})$. When you select the folded power transformation, a plot of 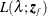$L(\lambda ;\bm {z}_{\scriptscriptstyle f})$ appears. You should choose a value close to the MLE value.