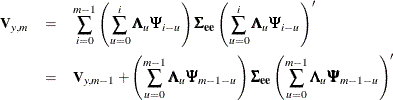The STATESPACE Procedure
Forecasting
Given estimates of 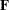 ,
, 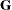 , and
, and 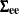 , forecasts of
, forecasts of 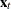 are computed from the conditional expectation of
are computed from the conditional expectation of 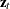 .
.
In forecasting, the parameters F, G, and 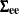 are replaced with the estimates or by values specified in the RESTRICT statement. One-step-ahead forecasting is performed
for the observation
are replaced with the estimates or by values specified in the RESTRICT statement. One-step-ahead forecasting is performed
for the observation 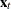 , where
, where 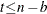 . Here
. Here  is the number of observations and b is the value of the BACK= option. For the observation
is the number of observations and b is the value of the BACK= option. For the observation 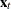 , where
, where 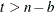 , m-step-ahead forecasting is performed for
, m-step-ahead forecasting is performed for 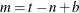 . The forecasts are generated recursively with the initial condition
. The forecasts are generated recursively with the initial condition 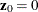 .
.
The m-step-ahead forecast of 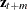 is
is 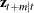 , where
, where 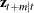 denotes the conditional expectation of
denotes the conditional expectation of 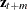 given the information available at time t. The m-step-ahead forecast of
given the information available at time t. The m-step-ahead forecast of 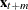 is
is 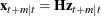 , where the matrix
, where the matrix ![${\mb{H} = [\mb{I}_{r} \mb{0} ]}$](images/etsug_statespa0154.png) .
.
Let 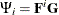 . Note that the last
. Note that the last  elements of
elements of 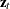 consist of the elements of
consist of the elements of 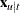 for
for 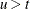 .
.
The state vector 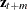 can be represented as
can be represented as
![\[ \mb{z}_{t+m} = \mb{F} ^{m} \mb{z}_{t} + \sum _{i=0}^{m-1}{\bPsi _{i} \mb{e}_{t+m-i}} \]](images/etsug_statespa0158.png)
Since 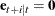 for
for 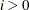 , the m-step-ahead forecast
, the m-step-ahead forecast 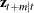 is
is
![\[ \mb{z}_{t+m|t} = \mb{F} ^{m} \mb{z}_{t} = \mb{F} \mb{z}_{t+m-1|t} \]](images/etsug_statespa0161.png)
Therefore, the m-step-ahead forecast of 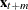 is
is
![\[ \mb{x}_{t+m|t} = \mb{H} \mb{z}_{t+m|t} \]](images/etsug_statespa0162.png)
The m-step-ahead forecast error is
![\[ \mb{z}_{t+m}-\mb{z}_{t+m|t} = \sum _{i=0}^{m-1}{\bPsi _{i} \mb{e}_{t+m-i}} \]](images/etsug_statespa0163.png)
The variance of the m-step-ahead forecast error is
![\[ \mb{V}_{z,m} = \sum _{i=0}^{m-1}{\bPsi _{i} \bSigma _{\mb{ee}} {\Psi }_{i}’} \]](images/etsug_statespa0164.png)
Letting 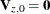 , the variance of the m-step-ahead forecast error of
, the variance of the m-step-ahead forecast error of 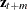 ,
, 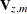 , can be computed recursively as follows:
, can be computed recursively as follows:
![\[ \mb{V}_{z,m} = \mb{V}_{z,m-1} + \bPsi _{m-1} \bSigma _{\mb{ee}} \bPsi ^{'}_{m-1} \]](images/etsug_statespa0167.png)
The variance of the m-step-ahead forecast error of 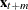 is the
is the  left upper submatrix of
left upper submatrix of 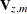 ; that is,
; that is,
![\[ \mb{V}_{x,m} = \mb{H} \mb{V}_{z,m}\mb{H} ’ \]](images/etsug_statespa0168.png)
Unless the NOCENTER option is specified, the sample mean vector is added to the forecast. When differencing is specified,
the forecasts x 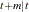 plus the sample mean vector are integrated back to produce forecasts for the original series.
plus the sample mean vector are integrated back to produce forecasts for the original series.
Let 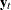 be the original series specified by the VAR statement, with some 0 values appended that correspond to the unobserved past
observations. Let B be the backshift operator, and let
be the original series specified by the VAR statement, with some 0 values appended that correspond to the unobserved past
observations. Let B be the backshift operator, and let 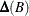 be the
be the  matrix polynomial in the backshift operator that corresponds to the differencing specified by the VAR statement. The off-diagonal
elements of
matrix polynomial in the backshift operator that corresponds to the differencing specified by the VAR statement. The off-diagonal
elements of 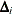 are 0. Note that
are 0. Note that 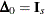 , where
, where 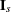 is the
is the  identity matrix. Then
identity matrix. Then 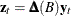 .
.
This gives the relationship
![\[ \mb{y}_{t} = \bDelta ^{-1}(B) \mb{z}_{t} = \sum _{i=0}^{{\infty }}{\bLambda _{i}\mb{z}_{t-i}} \]](images/etsug_statespa0176.png)
where 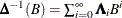 and
and 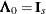 .
.
The m-step-ahead forecast of 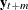 is
is
![\[ \mb{y}_{t+m|t} = \sum _{i=0}^{m-1}{\bLambda _{i} \mb{z}_{t+m-i|t}} + \sum _{i=m}^{{\infty }}{\bLambda _{i} \mb{z}_{t+m-i}} \]](images/etsug_statespa0180.png)
The m-step-ahead forecast error of 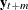 is
is
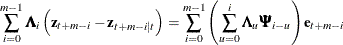
Letting 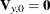 , the variance of the m-step-ahead forecast error of
, the variance of the m-step-ahead forecast error of 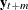 ,
, 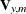 , is
, is