The STATESPACE Procedure

Canonical Correlation Analysis

Subsections:

State Vector Selection Process
Testing Significance of Canonical Correlations
Printing the Canonical Correlations
Preliminary Estimates of F

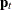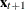Given the order p, let ${\mb{p}_{t}}$ be the vector of current and past values relevant to prediction of ${\mb{x}_{t+1}}$ :

$\mb{p}_{t}=( \mb{x} ’_{t}, \mb{x} ’_{t-1}, {\cdots }, \mb{x} ’_{t-p})’$

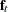Let ${\mb{f}_{t}}$ be the vector of current and future values:

$\mb{f}_{t}=( \mb{x} ’_{t}, \mb{x} ’_{t+1},{\cdots }, \mb{x} ’_{t+p})’$

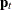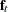In the canonical correlation analysis, consider submatrices of the sample covariance matrix of ${\mb{p}_{t}}$ and ${\mb{f}_{t}}$ . This covariance matrix, 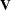${\mb{V}}$ , has a block Hankel form:

$\begin{eqnarray*} \Strong{V} =\left[\begin{matrix} \Strong{C}_{0} & \Strong{C} ’_{1} & \Strong{C} ’_{2} & {\cdots } & \Strong{C} ’_{p} \\ \Strong{C} ’_{1} & \Strong{C} ’_{2} & \Strong{C} ’_{3} & {\cdots } & \Strong{C} ’_{p+1} \\ {\vdots } & {\vdots } & {\vdots } & & {\vdots } \\ \Strong{C} ’_{p} & \Strong{C} ’_{p+1} & \Strong{C} ’_{p+2} & {\cdots } & \Strong{C} ’_{2p} \nonumber \end{matrix} \right] \end{eqnarray*}$

State Vector Selection Process

The canonical correlation analysis forms a sequence of potential state vectors 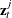${ \mb{z} ^{j}_{t}}$ . Examine a sequence 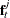${ \mb{f} ^{j}_{t}}$ of subvectors of 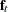${\mb{f}_{t}}$ , form the submatrix 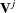${ \mb{V} ^{j}}$ that consists of the rows and columns of 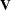${\mb{V}}$ that correspond to the components of 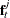${ \mb{f} ^{j}_{t}}$ , and compute its canonical correlations.

The smallest canonical correlation of 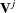${ \mb{V} ^{j}}$ is then used in the selection of the components of the state vector. The selection process is described in the following discussion. For more details about this process, see Akaike (1976).

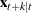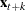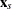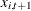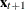In the following discussion, the notation ${\mb{x}_{t+k|t}}$ denotes the wide sense conditional expectation (best linear predictor) of ${\mb{x}_{t+k}}$ , given all ${\mb{x}_{s}}$ with s less than or equal to t. In the notation ${x_{i,t+1}}$ , the first subscript denotes the ith component of ${\mb{x}_{t+1}}$ .

The initial state vector 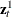${ \mb{z} ^{1}_{t}}$ is set to 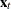${\mb{x}_{t}}$ . The sequence 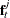${ \mb{f} ^{j}_{t}}$ is initialized by setting

$\mb{f} ^{1}_{t} = ( \mb{z} ^{1'}_{t}, x_{1,t+1|t})’ = ( \mb{x} ’_{t}, x_{1,t+1|t})’$

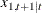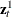That is, start by considering whether to add ${x_{1,t+1|t}}$ to the initial state vector ${ \mb{z} ^{1}_{t}}$ .

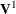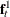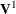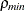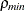The procedure forms the submatrix ${\mb{V} ^{1}}$ that corresponds to ${ \mb{f} ^{1}_{t}}$ and computes its canonical correlations. Denote the smallest canonical correlation of ${\mb{V} ^{1}}$ as ${{\rho }_{min}}$ . If ${{\rho }_{min}}$ is significantly greater than 0, 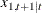${x_{1,t+1|t}}$ is added to the state vector.

If the smallest canonical correlation of 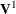${\mb{V} ^{1}}$ is not significantly greater than 0, then a linear combination of 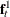${ \mb{f} ^{1}_{t}}$ is uncorrelated with the past, 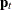${\mb{p}_{t}}$ . Assuming that the determinant of 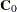${\mb{C}_{0}}$ is not 0, (that is, no input series is a constant), you can take the coefficient of 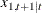${x_{1,t+1|t}}$ in this linear combination to be 1. Denote the coefficients of 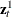${ \mb{z} ^{1}_{t}}$ in this linear combination as 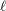${\mb{{\ell }}}$ . This gives the relationship:

$x_{1,t+1|t} = \mb{{\ell }}’\mb{x}_{t}$

Therefore, the current state vector already contains all the past information useful for predicting 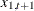${x_{1,t+1}}$ and any greater leads of 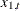${x_{1,t}}$ . The variable 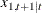${x_{1,t+1|t}}$ is not added to the state vector, nor are any terms 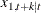${x_{1,t+k|t}}$ considered as possible components of the state vector. The variable 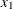${x_{1}}$ is no longer active for state vector selection.

The process described for 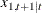${x_{1,t+1|t}}$ is repeated for the remaining elements of 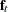${\mb{f}_{t}}$ . The next candidate for inclusion in the state vector is the next component of 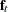${\mb{f}_{t}}$ that corresponds to an active variable. Components of 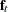${\mb{f}_{t}}$ that correspond to inactive variables that produced a zero 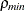${{\rho }_{min}}$ in a previous step are skipped.

Denote the next candidate as 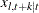${x_{l,t+k|t}}$ . The vector 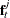${ \mb{f} ^{j}_{t}}$ is formed from the current state vector and 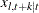${x_{l,t+k|t}}$ as follows:

${ \mb{f} ^{j}_{t}} = ( \mb{z} ^{j'}_{t}, x_{l,t+k|t} )’$

The matrix 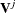${\mb{V} ^{j}}$ is formed from 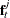${ \mb{f} ^{j}_{t}}$ and its canonical correlations are computed. The smallest canonical correlation of 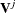${\mb{V} ^{j}}$ is judged to be either greater than or equal to 0. If it is judged to be greater than 0, 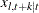${x_{l,t+k|t}}$ is added to the state vector. If it is judged to be 0, then a linear combination of 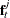${ \mb{f} ^{j}_{t}}$ is uncorrelated with the 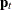${\mb{p}_{t}}$ , and the variable 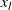${x_{l}}$ is now inactive.

The state vector selection process continues until no active variables remain.

Testing Significance of Canonical Correlations

For each step in the canonical correlation sequence, the significance of the smallest canonical correlation 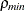${{\rho }_{min}}$ is judged by an information criterion from Akaike (1976). This information criterion is

$-n {\ln }( 1- {\rho }^{2}_{min} )-{\lambda }( r (p+1)-q+1 )$

where q is the dimension of 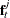${ \mb{f} ^{j}_{t}}$ at the current step, r is the order of the state vector, p is the order of the vector autoregressive process, and 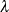${\lambda }$ is the value of the SIGCORR= option. The default is SIGCORR=2. If this information criterion is less than or equal to 0, 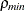${{\rho }_{min}}$ is taken to be 0; otherwise, it is taken to be significantly greater than 0. (Do not confuse this information criterion with the AIC.)

Variables in 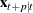${\mb{x}_{t+p|t}}$ are not added in the model, even with positive information criterion, because of the singularity of 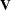${\mb{V}}$ . You can force the consideration of more candidate state variables by increasing the size of the 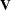${\mb{V}}$ matrix by specifying a PASTMIN= option value larger than p.

Printing the Canonical Correlations

To print the details of the canonical correlation analysis process, specify the CANCORR option in the PROC STATESPACE statement. The CANCORR option prints the candidate state vectors, the canonical correlations, and the information criteria for testing the significance of the smallest canonical correlation.

Bartlett’s 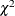${{\chi }^{2}}$ and its degrees of freedom are also printed when the CANCORR option is specified. The formula used for Bartlett’s 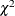${{\chi }^{2}}$ is

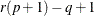${\chi }^{2} = - ( n-.5 ( r (p+1)-q+1 ) ) {\ln }( 1- {\rho }^{2}_{min} )$

with ${r (p+1)-q+1}$ degrees of freedom.

Figure 35.12 shows the output of the CANCORR option for the introductory example shown in the Getting Started: STATESPACE Procedure.

proc statespace data=in out=out lead=10 cancorr;
   var x(1) y(1);
   id t;
run;

Figure 35.12: Canonical Correlations Analysis

The STATESPACE Procedure

Canonical Correlations Analysis

x(T;T)	y(T;T)	x(T+1;T)	Information Criterion	Chi-Square	DF
1	1	0.237045	3.566167	11.4505	4

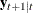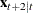New variables are added to the state vector if the information criteria are positive. In this example, $\mb{y}_{t+1|t}$ and $\mb{x}_{t+2|t}$ are not added to the state space vector because the information criteria for these models are negative.

If the information criterion is nearly 0, then you might want to investigate models that arise if the opposite decision is made regarding 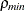${{\rho }_{min}}$ . This investigation can be accomplished by using a FORM statement to specify part or all of the state vector.

Preliminary Estimates of F

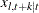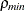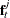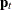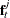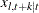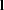When a candidate variable ${x_{l,t+k|t}}$ yields a zero ${{\rho }_{min}}$ and is not added to the state vector, a linear combination of ${ \mb{f} ^{j}_{t}}$ is uncorrelated with the ${\mb{p}_{t}}$ . Because of the method used to construct the ${ \mb{f} ^{j}_{t}}$ sequence, the coefficient of ${x_{l,t+k|t}}$ in ${\mb{l}}$ can be taken as 1. Denote the coefficients of 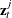${ \mb{z} ^{j}_{t}}$ in this linear combination as ${\mb{l}}$ .

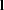This gives the relationship:

$x_{l,t+k|t} = \mb{l} ’ \mb{z} ^{j}_{t}$

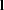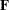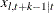The vector ${\mb{l}}$ is used as a preliminary estimate of the first r columns of the row of the transition matrix ${\mb{F}}$ corresponding to ${x_{l,t+k-1|t}}$ .