The COPULA Procedure

Canonical Maximum Likelihood Estimation (CMLE)

In the canonical maximum likelihood estimation (CMLE) method, it is assumed that the sample data 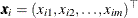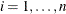$\pmb x_ i = ( x_{i1}, x_{i2}, \ldots , x_{im} )^\top $, $i=1,\ldots ,n$ have been transformed into uniform variates 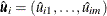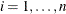$\boldsymbol {\hat{u}}_ i = (\hat{u}_{i1}, \ldots , \hat{u}_{im})$, $i=1,\ldots ,n$. One commonly used transformation is the nonparametric estimation of the CDF of the marginal distributions, which is closely related to empirical CDF,

\[ \hat{u}_{i,j}= \hat{F}_{j,n}(x_{i,j}) \]

where

\[ \hat{F}_{j,n}(x) = \frac{1}{n+1}\sum _{i=1}^ n I_{[x_{i,j}\le x]} \]

The transformed data 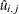$ \hat{u}_{i,j}$ are used as if they had uniform marginal distributions; hence, they are called pseudo-samples. The function 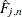$\hat{F}_{j,n}$ is different from the standard empirical CDF in the scalar 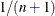$1/(n+1)$, which is to ensure that the transformed data cannot be on the boundary of the unit interval $[0,1]$. It is clear that

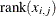\[ \hat{u}_{i,j} = \frac{1}{n+1} \textrm{rank}(x_{i,j}) \]

where $\textrm{rank}(x_{i,j})$ is the rank among 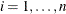$i=1,\ldots ,n$ in increasing order.

Let 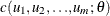$c(u_1, u_2, {\ldots }, u_ m; {\theta })$ be the density function of a copula 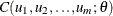$C(u_1, u_2,{\ldots }, u_ m; {\theta })$, and let 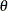$\theta $ be the parameter vector to be estimated. The parameter 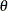$\theta $ is estimated by maximum likelihood:

\[ \hat{\theta } = \arg \max _{{\theta }\in {\Theta }} \sum _{i=1}^{n} \log c(\hat{u}_{i1}, {\ldots }, \hat{u}_{im}; {\theta }) \]