The AUTOREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics -
Examples

- References
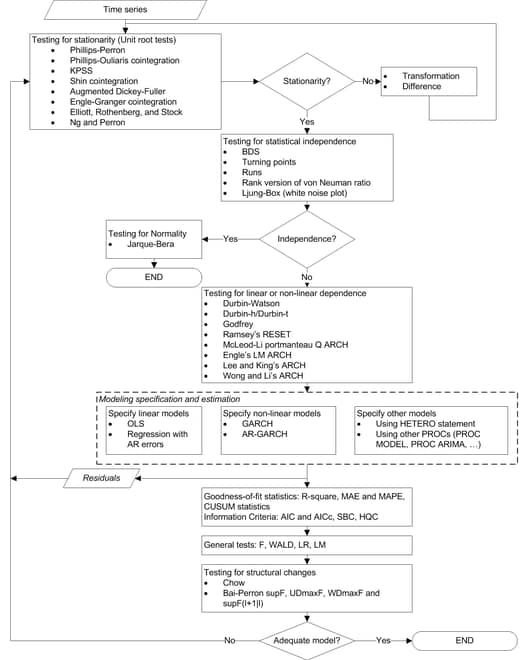
The modeling process consists of four stages: identification, specification, estimation, and diagnostic checking (Cromwell, Labys, and Terraza, 1994). The AUTOREG procedure supports tens of statistical tests for identification and diagnostic checking. Figure 8.15 illustrates how to incorporate these statistical tests into the modeling process.
Most of the theories of time series require stationarity; therefore, it is critical to determine whether a time series is stationary. Two nonstationary time series are fractionally integrated time series and autoregressive series with random coefficients. However, more often some time series are nonstationary due to an upward trend over time. The trend can be captured by either of the following two models.
-
The difference stationary process
![\[ (1- L)y_ t =\delta +\psi (L) \epsilon _ t \]](images/etsug_autoreg0402.png)
where
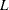 is the lag operator,
is the lag operator, 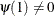 , and
, and 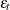 is a white noise sequence with mean zero and variance
is a white noise sequence with mean zero and variance 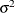 . Hamilton (1994) also refers to this model the unit root process.
. Hamilton (1994) also refers to this model the unit root process.
-
The trend stationary process
![\[ y_ t =\alpha +\delta t +\psi (L) \epsilon _ t \]](images/etsug_autoreg0406.png)
When a process has a unit root, it is said to be integrated of order one or I(1). An I(1) process is stationary after differencing once. The trend stationary process and difference stationary process require different treatment to transform the process into stationary one for analysis. Therefore, it is important to distinguish the two processes. Bhargava (1986) nested the two processes into the following general model
However, a difficulty is that the right-hand side is nonlinear in the parameters. Therefore, it is convenient to use a different parametrization
The test of null hypothesis that ![]() against the one-sided alternative of
against the one-sided alternative of ![]() is called a unit root test.
is called a unit root test.
Dickey-Fuller unit root tests are based on regression models similar to the previous model
where ![]() is assumed to be white noise. The t statistic of the coefficient
is assumed to be white noise. The t statistic of the coefficient ![]() does not follow the normal distribution asymptotically. Instead, its distribution can be derived using the functional central
limit theorem. Three types of regression models including the preceding one are considered by the Dickey-Fuller test. The
deterministic terms that are included in the other two types of regressions are either null or constant only.
does not follow the normal distribution asymptotically. Instead, its distribution can be derived using the functional central
limit theorem. Three types of regression models including the preceding one are considered by the Dickey-Fuller test. The
deterministic terms that are included in the other two types of regressions are either null or constant only.
An assumption in the Dickey-Fuller unit root test is that it requires the errors in the autoregressive model to be white noise, which is often not true. There are two popular ways to account for general serial correlation between the errors. One is the augmented Dickey-Fuller (ADF) test, which uses the lagged difference in the regression model. This was originally proposed by Dickey and Fuller (1979) and later studied by Said and Dickey (1984) and Phillips and Perron (1988). Another method is proposed by Phillips and Perron (1988); it is called Phillips-Perron (PP) test. The tests adopt the original Dickey-Fuller regression with intercept, but modify the test statistics to take account of the serial correlation and heteroscedasticity. It is called nonparametric because no specific form of the serial correlation of the errors is assumed.
A problem of the augmented Dickey-Fuller and Phillips-Perron unit root tests is that they are subject to size distortion and low power. It is reported in Schwert (1989) that the size distortion is significant when the series contains a large moving average (MA) parameter. DeJong et al. (1992) find that the ADF has power around one third and PP test has power less than 0.1 against the trend stationary alternative, in some common settings. Among some more recent unit root tests that improve upon the size distortion and the low power are the tests described by Elliott, Rothenberg, and Stock (1996) and Ng and Perron (2001). These tests involve a step of detrending before constructing the test statistics and are demonstrated to perform better than the traditional ADF and PP tests.
Most testing procedures specify the unit root processes as the null hypothesis. Tests of the null hypothesis of stationarity have also been studied, among which Kwiatkowski et al. (1992) is very popular.
Economic theories often dictate that a group of economic time series are linked together by some long-run equilibrium relationship.
Statistically, this phenomenon can be modeled by cointegration. When several nonstationary processes ![]() are cointegrated, there exists a
are cointegrated, there exists a ![]() cointegrating vector
cointegrating vector ![]() such that
such that ![]() is stationary and
is stationary and ![]() is a nonzero vector. One way to test the relationship of cointegration is the residual based cointegration test, which assumes the regression model
is a nonzero vector. One way to test the relationship of cointegration is the residual based cointegration test, which assumes the regression model
where ![]() ,
, ![]() , and
, and ![]() = (
= (![]()
![]() ,
,![]() ,
,![]()
![]() . The OLS residuals from the regression model are used to test for the null hypothesis of no cointegration. Engle and Granger
(1987) suggest using ADF on the residuals while Phillips and Ouliaris (1990) study the tests using PP and other related test statistics.
. The OLS residuals from the regression model are used to test for the null hypothesis of no cointegration. Engle and Granger
(1987) suggest using ADF on the residuals while Phillips and Ouliaris (1990) study the tests using PP and other related test statistics.
Common unit root tests have the null hypothesis that there is an autoregressive unit root ![]() , and the alternative is
, and the alternative is ![]() , where
, where ![]() is the autoregressive coefficient of the time series
is the autoregressive coefficient of the time series
This is referred to as the zero mean model. The standard Dickey-Fuller (DF) test assumes that errors ![]() are white noise. There are two other types of regression models that include a constant or a time trend as follows:
are white noise. There are two other types of regression models that include a constant or a time trend as follows:
These two models are referred to as the constant mean model and the trend model, respectively. The constant mean model includes
a constant mean ![]() of the time series. However, the interpretation of
of the time series. However, the interpretation of ![]() depends on the stationarity in the following sense: the mean in the stationary case when
depends on the stationarity in the following sense: the mean in the stationary case when ![]() is the trend in the integrated case when
is the trend in the integrated case when ![]() . Therefore, the null hypothesis should be the joint hypothesis that
. Therefore, the null hypothesis should be the joint hypothesis that ![]() and
and ![]() . However for the unit root tests, the test statistics are concerned with the null hypothesis of
. However for the unit root tests, the test statistics are concerned with the null hypothesis of ![]() . The joint null hypothesis is not commonly used. This issue is address in Bhargava (1986) with a different nesting model.
. The joint null hypothesis is not commonly used. This issue is address in Bhargava (1986) with a different nesting model.
There are two types of test statistics. The conventional t ratio is
and the second test statistic, called ![]() -test, is
-test, is
For the zero mean model, the asymptotic distributions of the Dickey-Fuller test statistics are
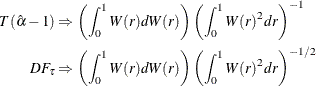
For the constant mean model, the asymptotic distributions are
![\begin{align*} T(\hat{\alpha }-1) & \Rightarrow \left( [W(1)^2-1]/2 -W(1)\int _0^1 W(r)dr \right)\left( \int _0^1 W(r)^2 dr - \left(\int _0^1 W(r)dr \right)^2\right)^{-1}\\ DF_\tau & \Rightarrow \left([W(1)^2-1]/2 -W(1)\int _0^1 W(r)dr \right)\left( \int _0^1 W(r)^2 dr - \left(\int _0^1 W(r)dr \right)^2\right)^{-1/2} \end{align*}](images/etsug_autoreg0432.png)
For the trend model, the asymptotic distributions are
![\begin{equation*} \begin{split} T(\hat{\alpha }-1) & \Rightarrow \left[ W(r)dW +12\left(\int _0^1 rW(r)dr -\frac{1}{2}\int _0^1 W(r)dr \right) \left( \int _0^1 W(r)dr - \frac12 W(1)\right) \right. \\ & \quad \left. -W(1) \int _0^1 W(r)dr \right] D^{-1} \\ DF_\tau & \Rightarrow \left[ W(r)dW +12\left(\int _0^1 rW(r)dr -\frac{1}{2}\int _0^1 W(r)dr \right) \left( \int _0^1 W(r)dr - \frac12 W(1)\right) \right. \\ & \quad \left. -W(1) \int _0^1 W(r)dr \right] D^{1/2} \end{split}\end{equation*}](images/etsug_autoreg0433.png)
where
One problem of the Dickey-Fuller and similar tests that employ three types of regressions is the difficulty in the specification of the deterministic trends. Campbell and Perron (1991) claimed that "the proper handling of deterministic trends is a vital prerequisite for dealing with unit roots". However the "proper handling" is not obvious since the distribution theory of the relevant statistics about the deterministic trends is not available. Hayashi (2000) suggests to using the constant mean model when you think there is no trend, and using the trend model when you think otherwise. However no formal procedure is provided.
The null hypothesis of the Dickey-Fuller test is a random walk, possibly with drift. The differenced process is not serially correlated under the null of I(1). There is a great need for the generalization of this specification. The augmented Dickey-Fuller (ADF) test, originally proposed in Dickey and Fuller (1979), adjusts for the serial correlation in the time series by adding lagged first differences to the autoregressive model,
where the deterministic terms ![]() and
and ![]() can be absent for the models without drift or linear trend. As previously, there are two types of test statistics. One is
the OLS t value
can be absent for the models without drift or linear trend. As previously, there are two types of test statistics. One is
the OLS t value
and the other is given by
The asymptotic distributions of the test statistics are the same as those of the standard Dickey-Fuller test statistics.
Nonstationary multivariate time series can be tested for cointegration, which means that a linear combination of these time
series is stationary. Formally, denote the series by ![]() . The null hypothesis of cointegration is that there exists a vector
. The null hypothesis of cointegration is that there exists a vector ![]() such that
such that ![]() is stationary. Residual-based cointegration tests were studied in Engle and Granger (1987) and Phillips and Ouliaris (1990). The latter are described in the next subsection. The first step regression is
is stationary. Residual-based cointegration tests were studied in Engle and Granger (1987) and Phillips and Ouliaris (1990). The latter are described in the next subsection. The first step regression is
where ![]() ,
, ![]() , and
, and ![]() = (
= (![]()
![]() ,
,![]() ,
,![]()
![]() . This regression can also include an intercept or an intercept with a linear trend. The residuals are used to test for the
existence of an autoregressive unit root. Engle and Granger (1987) proposed augmented Dickey-Fuller type regression without an intercept on the residuals to test the unit root. When the first
step OLS does not include an intercept, the asymptotic distribution of the ADF test statistic
. This regression can also include an intercept or an intercept with a linear trend. The residuals are used to test for the
existence of an autoregressive unit root. Engle and Granger (1987) proposed augmented Dickey-Fuller type regression without an intercept on the residuals to test the unit root. When the first
step OLS does not include an intercept, the asymptotic distribution of the ADF test statistic ![]() is given by
is given by
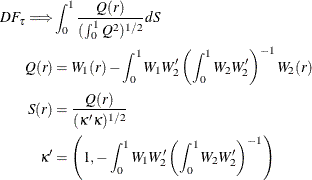
where ![]() is a k vector standard Brownian motion and
is a k vector standard Brownian motion and
is a partition such that ![]() is a scalar and
is a scalar and ![]() is
is ![]() dimensional. The asymptotic distributions of the test statistics in the other two cases have the same form as the preceding
formula. If the first step regression includes an intercept, then
dimensional. The asymptotic distributions of the test statistics in the other two cases have the same form as the preceding
formula. If the first step regression includes an intercept, then ![]() is replaced by the demeaned Brownian motion
is replaced by the demeaned Brownian motion ![]() . If the first step regression includes a time trend, then
. If the first step regression includes a time trend, then ![]() is replaced by the detrended Brownian motion. The critical values of the asymptotic distributions are tabulated in Phillips
and Ouliaris (1990) and MacKinnon (1991).
is replaced by the detrended Brownian motion. The critical values of the asymptotic distributions are tabulated in Phillips
and Ouliaris (1990) and MacKinnon (1991).
The residual based cointegration tests have a major shortcoming. Different choices of the dependent variable in the first
step OLS might produce contradictory results. This can be explained theoretically. If the dependent variable is in the cointegration
relationship, then the test is consistent against the alternative that there is cointegration. On the other hand, if the dependent
variable is not in the cointegration system, the OLS residual ![]() do not converge to a stationary process. Changing the dependent variable is more likely to produce conflicting results in
finite samples.
do not converge to a stationary process. Changing the dependent variable is more likely to produce conflicting results in
finite samples.
Besides the ADF test, there is another popular unit root test that is valid under general serial correlation and heteroscedasticity,
developed by Phillips (1987) and Phillips and Perron (1988). The tests are constructed using the AR(1) type regressions, unlike ADF tests, with corrected estimation of the long run
variance of ![]() . In the case without intercept, consider the driftless random walk process
. In the case without intercept, consider the driftless random walk process
where the disturbances might be serially correlated with possible heteroscedasticity. Phillips and Perron (1988) proposed the unit root test of the OLS regression model,
Denote the OLS residual by ![]() . The asymptotic variance of
. The asymptotic variance of ![]() can be estimated by using the truncation lag l.
can be estimated by using the truncation lag l.
where ![]() ,
, ![]() for
for ![]() , and
, and ![]() . This is a consistent estimator suggested by Newey and West (1987).
. This is a consistent estimator suggested by Newey and West (1987).
The variance of ![]() can be estimated by
can be estimated by ![]() . Let
. Let ![]() be the variance estimate of the OLS estimator
be the variance estimate of the OLS estimator ![]() . Then the Phillips-Perron
. Then the Phillips-Perron ![]() test (zero mean case) is written
test (zero mean case) is written
The ![]() statistic is just the ordinary Dickey-Fuller
statistic is just the ordinary Dickey-Fuller ![]() statistic with a correction term that accounts for the serial correlation. The correction term goes to zero asymptotically
if there is no serial correlation.
statistic with a correction term that accounts for the serial correlation. The correction term goes to zero asymptotically
if there is no serial correlation.
Note that ![]() as
as ![]() , which shows that the limiting distribution is skewed to the left.
, which shows that the limiting distribution is skewed to the left.
Let ![]() be the
be the ![]() statistic for
statistic for ![]() . The Phillips-Perron
. The Phillips-Perron ![]() (defined here as
(defined here as ![]() ) test is written
) test is written
To incorporate a constant intercept, the regression model ![]() is used (single mean case) and null hypothesis the series is a driftless random walk with nonzero unconditional mean. To
incorporate a time trend, we used the regression model
is used (single mean case) and null hypothesis the series is a driftless random walk with nonzero unconditional mean. To
incorporate a time trend, we used the regression model ![]() and under the null the series is a random walk with drift.
and under the null the series is a random walk with drift.
The limiting distributions of the test statistics for the zero mean case are
![\begin{align*} \hat{\mr{Z}}_{\rho } & \Rightarrow \frac{\frac{1}{2}\{ {\mi{B} (1)} ^{2}-1\} }{\int _{0}^{1}{{[\mi{B} (s)} ]^{2}ds}} \\ \hat{\mr{Z}}_\tau & \Rightarrow \frac{\frac{1}{2}\{ {[\mi{B} (1)} ]^{2}-1\} }{\{ \int _{0}^{1}{{[\mi{B} (x)} ]^{2}dx}\} ^{1/2} } \end{align*}](images/etsug_autoreg0473.png)
where B(![]() ) is a standard Brownian motion.
) is a standard Brownian motion.
The limiting distributions of the test statistics for the intercept case are
![\begin{align*} \hat{Z}_{\rho } & \Rightarrow \frac{\frac{1}{2}\{ {[\mi{B} (1)} ]^{2}-1\} -\mi{B} (1)\int _{0}^{1}{\mi{B} (x)dx}}{\int _{0}^{1}{{[\mi{B} (x)} ]^{2}dx} -\left[{\int _{0}^{1}{\mi{B} (x)dx}}\right]^{2}} \\ {\hat{\mr{Z}}_\tau } & \Rightarrow \frac{\frac{1}{2}\{ {[\mi{B} (1)} ]^{2}-1\} -\mi{B} (1)\int _{0}^{1}{\mi{B} (x)dx}}{{\{ \int _{0}^{1}{{[\mi{B} (x)}]^{2}dx} -\left[{\int _{0}^{1}{\mi{B} (x)dx}}\right]^{2} }\} ^{1/2} } \end{align*}](images/etsug_autoreg0475.png)
Finally, The limiting distributions of the test statistics for the trend case are can be derived as
![\[ \begin{bmatrix} 0 & c & 0 \end{bmatrix} V^{-1} \begin{bmatrix} \mi{B} (1) \\ \left({\mi{B} (1)}^{2}-1 \right)/2 \\ \mi{B} (1)-\int _{0}^{1}{\mi{B} (x)dx} \end{bmatrix} \]](images/etsug_autoreg0476.png)
where ![]() for
for ![]() and
and ![]() for
for ![]() ,
,
![\[ V = \left[\begin{matrix} 1 & \int _{0}^{1}{\mi{B} (x)dx} & 1/2 \\ \int _{0}^{1}{\mi{B} (x)dx} & \int _{0}^{1}{{\mi{B} (x)} ^{2}dx} & \int _{0}^{1}{x\mi{B} (x)dx} \\ 1/2 & \int _{0}^{1}{x\mi{B} (x)dx} & 1/3 \end{matrix}\right] \]](images/etsug_autoreg0479.png)
The finite sample performance of the PP test is not satisfactory ( see Hayashi (2000) ).
When several variables ![]() are cointegrated, there exists a
are cointegrated, there exists a ![]() cointegrating vector
cointegrating vector ![]() such that
such that ![]() is stationary and
is stationary and ![]() is a nonzero vector. The residual based cointegration test assumes the following regression model:
is a nonzero vector. The residual based cointegration test assumes the following regression model:
where ![]() ,
, ![]() , and
, and ![]() = (
= (![]()
![]() ,
,![]() ,
,![]()
![]() . You can estimate the consistent cointegrating vector by using OLS if all variables are difference stationary — that is,
I(1). The estimated cointegrating vector is
. You can estimate the consistent cointegrating vector by using OLS if all variables are difference stationary — that is,
I(1). The estimated cointegrating vector is ![]() . The Phillips-Ouliaris test is computed using the OLS residuals from the preceding regression model, and it uses the PP unit
root tests
. The Phillips-Ouliaris test is computed using the OLS residuals from the preceding regression model, and it uses the PP unit
root tests ![]() and
and ![]() developed in Phillips (1987), although in Phillips and Ouliaris (1990) the asymptotic distributions of some other leading unit root tests are also derived. The null hypothesis is no cointegration.
developed in Phillips (1987), although in Phillips and Ouliaris (1990) the asymptotic distributions of some other leading unit root tests are also derived. The null hypothesis is no cointegration.
You need to refer to the tables by Phillips and Ouliaris (1990) to obtain the p-value of the cointegration test. Before you apply the cointegration test, you may want to perform the unit root test for each variable (see the option STATIONARITY= ).
As in the Engle-Granger cointegration tests, the Phillips-Ouliaris test can give conflicting results for different choices of the regressand. There are other cointegration tests that are invariant to the order of the variables, including Johansen (1988), Johansen (1991), Stock and Watson (1988).
As mentioned earlier, ADF and PP both suffer severe size distortion and low power. There is a class of newer tests that improve both size and power. These are sometimes called efficient unit root tests, and among them tests by Elliott, Rothenberg, and Stock (1996) and Ng and Perron (2001) are prominent.
Elliott, Rothenberg, and Stock (1996) consider the data generating process
where ![]() is either
is either ![]() or
or ![]() and
and ![]() is an unobserved stationary zero-mean process with positive spectral density at zero frequency. The null hypothesis is
is an unobserved stationary zero-mean process with positive spectral density at zero frequency. The null hypothesis is ![]() , and the alternative is
, and the alternative is ![]() . The key idea of Elliott, Rothenberg, and Stock (1996) is to study the asymptotic power and asymptotic power envelope of some new tests. Asymptotic power is defined with a sequence
of local alternatives. For a fixed alternative hypothesis, the power of a test usually goes to one when sample size goes to
infinity; however, this says nothing about the finite sample performance. On the other hand, when the data generating process
under the alternative moves closer to the null hypothesis as the sample size increases, the power does not necessarily converge
to one. The local-to-unity alternatives in ERS are
. The key idea of Elliott, Rothenberg, and Stock (1996) is to study the asymptotic power and asymptotic power envelope of some new tests. Asymptotic power is defined with a sequence
of local alternatives. For a fixed alternative hypothesis, the power of a test usually goes to one when sample size goes to
infinity; however, this says nothing about the finite sample performance. On the other hand, when the data generating process
under the alternative moves closer to the null hypothesis as the sample size increases, the power does not necessarily converge
to one. The local-to-unity alternatives in ERS are
and the power against the local alternatives has a limit as ![]() goes to infinity, which is called asymptotic power. This value is strictly between 0 and 1. Asymptotic power indicates the
adequacy of a test to distinguish small deviations from the null hypothesis.
goes to infinity, which is called asymptotic power. This value is strictly between 0 and 1. Asymptotic power indicates the
adequacy of a test to distinguish small deviations from the null hypothesis.
Define
Let ![]() be the sum of squared residuals from a least squares regression of
be the sum of squared residuals from a least squares regression of ![]() on
on ![]() . Then the point optimal test against the local alternative
. Then the point optimal test against the local alternative ![]() has the form
has the form
where ![]() is an estimator for
is an estimator for ![]() . The test rejects the null when
. The test rejects the null when ![]() is small. The asymptotic power function for the point optimal test that is constructed with
is small. The asymptotic power function for the point optimal test that is constructed with ![]() under local alternatives with c is denoted by
under local alternatives with c is denoted by ![]() . Then the power envelope is
. Then the power envelope is ![]() because the test formed with
because the test formed with ![]() is the most powerful against the alternative
is the most powerful against the alternative ![]() . In other words, the asymptotic function
. In other words, the asymptotic function ![]() is always below the power envelope
is always below the power envelope ![]() except that at one point,
except that at one point, ![]() , they are tangent. Elliott, Rothenberg, and Stock (1996) show that choosing some specific values for
, they are tangent. Elliott, Rothenberg, and Stock (1996) show that choosing some specific values for ![]() can cause the asymptotic power function
can cause the asymptotic power function ![]() of the point optimal test to be very close to the power envelope. The optimal
of the point optimal test to be very close to the power envelope. The optimal ![]() is
is ![]() when
when ![]() , and
, and ![]() when
when ![]() . This choice of
. This choice of ![]() corresponds to the tangent point where
corresponds to the tangent point where ![]() . This is also true of the DF-GLS test.
. This is also true of the DF-GLS test.
Elliott, Rothenberg, and Stock (1996) also propose the DF-GLS test, given by the t statistic for testing ![]() in the regression
in the regression
where ![]() is obtained in a first step detrending
is obtained in a first step detrending
and ![]() is least squares regression coefficient of
is least squares regression coefficient of ![]() on
on ![]() . Regarding the lag length selection, Elliott, Rothenberg, and Stock (1996) favor the Schwarz Bayesian information criterion. The optimal selection of the lag length p and the estimation of
. Regarding the lag length selection, Elliott, Rothenberg, and Stock (1996) favor the Schwarz Bayesian information criterion. The optimal selection of the lag length p and the estimation of ![]() is further discussed in Ng and Perron (2001). The lag length is selected from the interval
is further discussed in Ng and Perron (2001). The lag length is selected from the interval ![]() for some fixed
for some fixed ![]() by using the modified Akaike’s information criterion,
by using the modified Akaike’s information criterion,
where ![]() and
and ![]() . For fixed lag length p, an estimate of
. For fixed lag length p, an estimate of ![]() is given by
is given by
![\[ \hat{\omega }^2= \frac{(T-1-p)^{-1} \sum _{t=p+2}^{T} \hat{\epsilon }_{tp}^2 }{ \left(1- \sum _{j=1}^ p \hat{\psi }_ j \right)^2} \]](images/etsug_autoreg0520.png)
DF-GLS is indeed a superior unit root test, according to Stock (1994), Schwert (1989), and Elliott, Rothenberg, and Stock (1996). In terms of the size of the test, DF-GLS is almost as good as the ADF t test ![]() and better than the PP
and better than the PP ![]() and
and ![]() test. In addition, the power of the DF-GLS test is greater than that of both the ADF t test and the
test. In addition, the power of the DF-GLS test is greater than that of both the ADF t test and the ![]() -test.
-test.
Ng and Perron (2001) also apply GLS detrending to obtain the following M-tests:
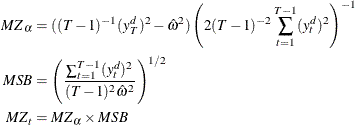
The first one is a modified version of the Phillips-Perron ![]() test,
test,
where the detrended data ![]() is used. The second is a modified Bhargava (1986)
is used. The second is a modified Bhargava (1986) ![]() test statistic. The third can be perceived as a modified Phillips-Perron
test statistic. The third can be perceived as a modified Phillips-Perron ![]() statistic because of the relationship
statistic because of the relationship ![]() .
.
The modified point optimal tests that use the GLS detrended data are
![\[ \begin{array}{ll} MP_ T^{GLS}=\frac{ \bar{c}^2(T-1)^{-2} \sum _{t=1}^{T-1} (y_{t}^ d)^2 -\bar{c} (T-1)^{-1} (y_{T}^ d)^2}{\hat{\omega }^2} \quad & \text {for} \; z_ t =1 \\ MP_ T^{GLS}=\frac{ \bar{c}^2(T-1)^{-2} \sum _{t=1}^{T-1} (y_{t}^ d)^2 +(1-\bar{c}) (T-1)^{-1} (y_{T}^ d)^2}{\hat{\omega }^2}\quad & \text {for}\; z_ t =(1,t) \\ \end{array} \]](images/etsug_autoreg0531.png)
The DF-GLS test and the ![]() test have the same limiting distribution:
test have the same limiting distribution:
![\[ \begin{array}{ll} \text {DF-GLS} \approx MZ_ t \Rightarrow 0.5\frac{(J_ c(1)^2 -1)}{ \left(\int _0^1 J_ c(r)^2dr \right)^{1/2}} \quad & \text {for} \; z_ t =1\\ \text {DF-GLS} \approx MZ_ t \Rightarrow 0.5\frac{(V_{c,\bar{c}}(1)^2 -1)}{\left( \int _0^1 V_{c,\bar{c}}(r)^2dr \right)^{1/2}} \quad & \text {for}\; z_ t =(1,t)\\ \end{array} \]](images/etsug_autoreg0533.png)
The point optimal test and the modified point optimal test have the same limiting distribution:
where ![]() is a standard Brownian motion and
is a standard Brownian motion and ![]() is an Ornstein-Uhlenbeck process defined by
is an Ornstein-Uhlenbeck process defined by ![]() with
with ![]() ,
, ![]() , and
, and ![]() .
.
Overall, the M-tests have the smallest size distortion, with the ADF t test having the next smallest. The ADF ![]() -test,
-test, ![]() , and
, and ![]() have the largest size distortion. In addition, the power of the DF-GLS and M-tests is greater than that of the ADF t test and
have the largest size distortion. In addition, the power of the DF-GLS and M-tests is greater than that of the ADF t test and ![]() -test. The ADF
-test. The ADF ![]() has more severe size distortion than the ADF
has more severe size distortion than the ADF ![]() , but it has more power for a fixed lag length.
, but it has more power for a fixed lag length.
There are fewer tests available for the null hypothesis of trend stationarity I(0). The main reason is the difficulty of theoretical
development. The KPSS test was introduced in Kwiatkowski et al. (1992) to test the null hypothesis that an observable series is stationary around a deterministic trend. For consistency, the notation
used here differs from the notation in the original paper. The setup of the problem is as follows: it is assumed that the
series is expressed as the sum of the deterministic trend, random walk ![]() , and stationary error
, and stationary error ![]() ; that is,
; that is,
where ![]() iid
iid ![]() , and an intercept
, and an intercept ![]() (in the original paper, the authors use
(in the original paper, the authors use ![]() instead of
instead of ![]() ; here we assume
; here we assume ![]() .) The null hypothesis of trend stationarity is specified by
.) The null hypothesis of trend stationarity is specified by ![]() , while the null of level stationarity is the same as above with the model restriction
, while the null of level stationarity is the same as above with the model restriction ![]() . Under the alternative that
. Under the alternative that ![]() , there is a random walk component in the observed series
, there is a random walk component in the observed series ![]() .
.
Under stronger assumptions of normality and iid of ![]() and
and ![]() , a one-sided LM test of the null that there is no random walk (
, a one-sided LM test of the null that there is no random walk (![]() ) can be constructed as follows:
) can be constructed as follows:
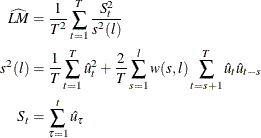
Under the null hypothesis, ![]() can be estimated by ordinary least squares regression of
can be estimated by ordinary least squares regression of ![]() on an intercept and the time trend. Following the original work of Kwiatkowski et al. (1992), under the null (
on an intercept and the time trend. Following the original work of Kwiatkowski et al. (1992), under the null (![]() ), the
), the ![]() statistic converges asymptotically to three different distributions depending on whether the model is trend-stationary, level-stationary
(
statistic converges asymptotically to three different distributions depending on whether the model is trend-stationary, level-stationary
(![]() ), or zero-mean stationary (
), or zero-mean stationary (![]() ,
, ![]() ). The trend-stationary model is denoted by subscript
). The trend-stationary model is denoted by subscript ![]() and the level-stationary model is denoted by subscript
and the level-stationary model is denoted by subscript ![]() . The case when there is no trend and zero intercept is denoted as 0. The last case, although rarely used in practice, is
considered in Hobijn, Franses, and Ooms (2004):
. The case when there is no trend and zero intercept is denoted as 0. The last case, although rarely used in practice, is
considered in Hobijn, Franses, and Ooms (2004):
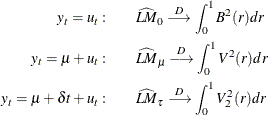
with
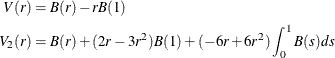
where ![]() is a Brownian motion (Wiener process) and
is a Brownian motion (Wiener process) and ![]() is convergence in distribution.
is convergence in distribution. ![]() is a standard Brownian bridge, and
is a standard Brownian bridge, and ![]() is a second-level Brownian bridge.
is a second-level Brownian bridge.
Using the notation of Kwiatkowski et al. (1992), the ![]() statistic is named as
statistic is named as ![]() . This test depends on the computational method used to compute the long-run variance
. This test depends on the computational method used to compute the long-run variance ![]() ; that is, the window width l and the kernel type
; that is, the window width l and the kernel type ![]() . You can specify the kernel used in the test by using the KERNEL option:
. You can specify the kernel used in the test by using the KERNEL option:
-
Newey-West/Bartlett (KERNEL=NW
 BART) (this is the default)
BART) (this is the default)
![\[ w(s,l)=1-\frac{s}{l+1} \]](images/etsug_autoreg0120.png)
-
quadratic spectral (KERNEL=QS)
![\[ w(s,l) = \tilde{w}\left(\frac sl\right)=\tilde{w}(x)=\frac{25}{12\pi ^2 x^2}\left(\frac{\sin \left(6\pi x/5\right)}{6\pi x/5}-\cos \left( \frac65\pi x\right)\right) \]](images/etsug_autoreg0567.png)
You can specify the number of lags, l, in three different ways:
-
Schwert (SCHW = c) (default for NW, c=12)
![\[ l=\max \left\{ 1,\text {floor}\left[c\left(\frac{T}{100}\right)^{1/4}\right]\right\} \]](images/etsug_autoreg0122.png)
-
manual (LAG = l)
-
automatic selection (AUTO) (default for QS), from Hobijn, Franses, and Ooms (2004). The number of lags, l, is calculated as in the following table:
KERNEL=NW
KERNEL=QS
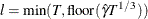
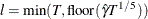
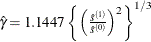
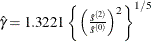
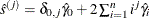
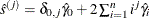
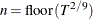
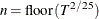
where
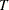 is the number of observations,
is the number of observations, 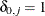 if
if  and 0 otherwise, and
and 0 otherwise, and 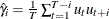 .
.
Simulation evidence shows that the KPSS has size distortion in finite samples. For an example, see Caner and Kilian (2001). The power is reduced when the sample size is large; this can be derived theoretically (see Breitung (1995)). Another problem of the KPSS test is that the power depends on the truncation lag used in the Newey-West estimator of the
long-run variance ![]() .
.
Shin (1994) extends the KPSS test to incorporate the regressors to be a cointegration test. The cointegrating regression becomes
where ![]() and
and ![]() are scalar and m-vector
are scalar and m-vector ![]() variables. There are still three cases of cointegrating regressions: without intercept and trend, with intercept only, and
with intercept and trend. The null hypothesis of the cointegration test is the same as that for the KPSS test,
variables. There are still three cases of cointegrating regressions: without intercept and trend, with intercept only, and
with intercept and trend. The null hypothesis of the cointegration test is the same as that for the KPSS test, ![]() . The test statistics for cointegration in the three cases of cointegrating regressions are exactly the same as those in the
KPSS test; these test statistics are then ignored here. Under the null hypothesis, the statistics converge asymptotically
to three different distributions:
. The test statistics for cointegration in the three cases of cointegrating regressions are exactly the same as those in the
KPSS test; these test statistics are then ignored here. Under the null hypothesis, the statistics converge asymptotically
to three different distributions:
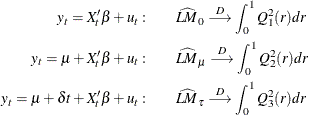
with
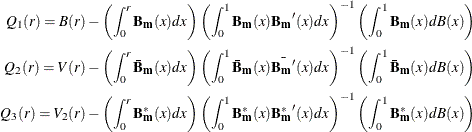
where ![]() and
and ![]() are independent scalar and m-vector standard Brownian motion, and
are independent scalar and m-vector standard Brownian motion, and ![]() is convergence in distribution.
is convergence in distribution. ![]() is a standard Brownian bridge,
is a standard Brownian bridge, ![]() is a Brownian bridge of a second-level,
is a Brownian bridge of a second-level, ![]() is an m-vector standard demeaned Brownian motion, and
is an m-vector standard demeaned Brownian motion, and ![]() is an m-vector standard demeaned and detrended Brownian motion.
is an m-vector standard demeaned and detrended Brownian motion.
The p-values that are reported for the KPSS test and Shin test are calculated via a Monte Carlo simulation of the limiting distributions, using a sample size of 2,000 and 1,000,000 replications.
Independence tests are widely used in model selection, residual analysis, and model diagnostics because models are usually based on the assumption of independently distributed errors. If a given time series (for example, a series of residuals) is independent, then no deterministic model is necessary for this completely random process; otherwise, there must exist some relationship in the series to be addressed. In the following section, four independence tests are introduced: the BDS test, the runs test, the turning point test, and the rank version of von Neumann ratio test.
Brock, Dechert, and Scheinkman (1987) propose a test (BDS test) of independence based on the correlation dimension. Brock et al. (1996) show that the first-order asymptotic distribution of the test statistic is independent of the estimation error provided
that the parameters of the model under test can be estimated ![]() -consistently. Hence, the BDS test can be used as a model selection tool and as a specification test.
-consistently. Hence, the BDS test can be used as a model selection tool and as a specification test.
Given the sample size ![]() , the embedding dimension m, and the value of the radius r, the BDS statistic is
, the embedding dimension m, and the value of the radius r, the BDS statistic is
where
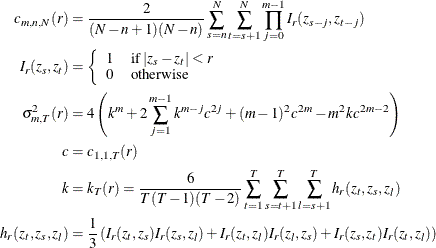
The statistic has a standard normal distribution if the sample size is large enough. For small sample size, the distribution can be approximately obtained through simulation. Kanzler (1999) has a comprehensive discussion on the implementation and empirical performance of BDS test.
The runs test and turning point test are two widely used tests for independence (Cromwell, Labys, and Terraza, 1994).
The runs test needs several steps. First, convert the original time series into the sequence of signs, ![]() , that is, map
, that is, map ![]() into
into ![]() where
where ![]() is the sample mean of
is the sample mean of ![]() and
and ![]() is "
is "![]() " if x is nonnegative and "
" if x is nonnegative and "![]() " if x is negative. Second, count the number of runs, R, in the sequence. A run of a sequence is a maximal non-empty segment of the sequence that consists of adjacent equal elements.
For example, the following sequence contains
" if x is negative. Second, count the number of runs, R, in the sequence. A run of a sequence is a maximal non-empty segment of the sequence that consists of adjacent equal elements.
For example, the following sequence contains ![]() runs:
runs:
Third, count the number of pluses and minuses in the sequence and denote them as ![]() and
and ![]() , respectively. In the preceding example sequence,
, respectively. In the preceding example sequence, ![]() and
and ![]() . Note that the sample size
. Note that the sample size ![]() . Finally, compute the statistic of runs test,
. Finally, compute the statistic of runs test,
where
The statistic of the turning point test is defined as follows:
where the indicator function of the turning point ![]() is 1 if
is 1 if ![]() or
or ![]() (that is, both the previous and next values are greater or less than the current value); otherwise, 0.
(that is, both the previous and next values are greater or less than the current value); otherwise, 0.
The statistics of both the runs test and the turning point test have the standard normal distribution under the null hypothesis of independence.
Since the runs test completely ignores the magnitudes of the observations, Bartels (1982) proposes a rank version of the von Neumann Ratio test for independence:
where ![]() is the rank of tth observation in the sequence of
is the rank of tth observation in the sequence of ![]() observations. For large sample, the statistic follows the standard normal distribution under the null hypothesis of independence.
For small samples of size between 11 and 100, the critical values through simulation would be more precise; for samples of
size no more than 10, the exact CDF is applied.
observations. For large sample, the statistic follows the standard normal distribution under the null hypothesis of independence.
For small samples of size between 11 and 100, the critical values through simulation would be more precise; for samples of
size no more than 10, the exact CDF is applied.
Based on skewness and kurtosis, Jarque and Bera (1980) calculated the test statistic
where
The ![]()
![]() (2) distribution gives an approximation to the normality test
(2) distribution gives an approximation to the normality test ![]() .
.
When the GARCH model is estimated, the normality test is obtained using the standardized residuals ![]() . The normality test can be used to detect misspecification of the family of ARCH models.
. The normality test can be used to detect misspecification of the family of ARCH models.
Consider the following linear regression model:
where ![]() is an
is an ![]() data matrix,
data matrix, ![]() is a
is a ![]() coefficient vector, and
coefficient vector, and ![]() is a
is a ![]() disturbance vector. The error term
disturbance vector. The error term ![]() is assumed to be generated by the jth-order autoregressive process
is assumed to be generated by the jth-order autoregressive process ![]() where
where ![]() ,
, ![]() is a sequence of independent normal error terms with mean 0 and variance
is a sequence of independent normal error terms with mean 0 and variance ![]() . Usually, the Durbin-Watson statistic is used to test the null hypothesis
. Usually, the Durbin-Watson statistic is used to test the null hypothesis ![]() against
against ![]() . Vinod (1973) generalized the Durbin-Watson statistic:
. Vinod (1973) generalized the Durbin-Watson statistic:
where ![]() are OLS residuals. Using the matrix notation,
are OLS residuals. Using the matrix notation,
where ![]() and
and ![]() is a
is a ![]() matrix:
matrix:
![\[ \mb{A} _{j} = \begin{bmatrix} -1 & 0 & {\cdots } & 0 & 1 & 0 & {\cdots } & 0 \\ 0 & -1 & 0 & {\cdots } & 0 & 1 & 0 & {\cdots } \\ {\vdots } & {\vdots } & {\vdots } & {\vdots } & {\vdots } & {\vdots } & {\vdots } & {\vdots } \\ 0 & {\cdots } & 0 & -1 & 0 & {\cdots } & 0 & 1 \end{bmatrix} \]](images/etsug_autoreg0636.png)
and there are ![]() zeros between
zeros between ![]() and 1 in each row of matrix
and 1 in each row of matrix ![]() .
.
The QR factorization of the design matrix ![]() yields a
yields a ![]() orthogonal matrix
orthogonal matrix ![]() :
:
where R is an ![]() upper triangular matrix. There exists an
upper triangular matrix. There exists an ![]() submatrix of
submatrix of ![]() such that
such that ![]() and
and ![]() . Consequently, the generalized Durbin-Watson statistic is stated as a ratio of two quadratic forms:
. Consequently, the generalized Durbin-Watson statistic is stated as a ratio of two quadratic forms:
where ![]() are upper n eigenvalues of
are upper n eigenvalues of ![]() and
and ![]() is a standard normal variate, and
is a standard normal variate, and ![]() . These eigenvalues are obtained by a singular value decomposition of
. These eigenvalues are obtained by a singular value decomposition of ![]() (Golub and Van Loan, 1989; Savin and White, 1978).
(Golub and Van Loan, 1989; Savin and White, 1978).
The marginal probability (or p-value) for ![]() given
given ![]() is
is
where
When the null hypothesis ![]() holds, the quadratic form
holds, the quadratic form ![]() has the characteristic function
has the characteristic function
The distribution function is uniquely determined by this characteristic function:
For example, to test ![]() given
given ![]() against
against ![]() , the marginal probability (p-value) can be used:
, the marginal probability (p-value) can be used:
where
and ![]() is the calculated value of the fourth-order Durbin-Watson statistic.
is the calculated value of the fourth-order Durbin-Watson statistic.
In the Durbin-Watson test, the marginal probability indicates positive autocorrelation (![]() ) if it is less than the level of significance (
) if it is less than the level of significance (![]() ), while you can conclude that a negative autocorrelation (
), while you can conclude that a negative autocorrelation (![]() ) exists if the marginal probability based on the computed Durbin-Watson statistic is greater than
) exists if the marginal probability based on the computed Durbin-Watson statistic is greater than ![]() . Wallis (1972) presented tables for bounds tests of fourth-order autocorrelation, and Vinod (1973) has given tables for a 5% significance level for orders two to four. Using the AUTOREG procedure, you can calculate the
exact p-values for the general order of Durbin-Watson test statistics. Tests for the absence of autocorrelation of order p can be performed sequentially; at the jth step, test
. Wallis (1972) presented tables for bounds tests of fourth-order autocorrelation, and Vinod (1973) has given tables for a 5% significance level for orders two to four. Using the AUTOREG procedure, you can calculate the
exact p-values for the general order of Durbin-Watson test statistics. Tests for the absence of autocorrelation of order p can be performed sequentially; at the jth step, test ![]() given
given ![]() against
against ![]() . However, the size of the sequential test is not known.
. However, the size of the sequential test is not known.
The Durbin-Watson statistic is computed from the OLS residuals, while that of the autoregressive error model uses residuals that are the difference between the predicted values and the actual values. When you use the Durbin-Watson test from the residuals of the autoregressive error model, you must be aware that this test is only an approximation. See Autoregressive Error Model earlier in this chapter. If there are missing values, the Durbin-Watson statistic is computed using all the nonmissing values and ignoring the gaps caused by missing residuals. This does not affect the significance level of the resulting test, although the power of the test against certain alternatives may be adversely affected. Savin and White (1978) have examined the use of the Durbin-Watson statistic with missing values.
The Durbin-Watson probability calculations have been enhanced to compute the p-value of the generalized Durbin-Watson statistic for large sample sizes. Previously, the Durbin-Watson probabilities were only calculated for small sample sizes.
Consider the following linear regression model:
where ![]() is an
is an ![]() data matrix,
data matrix, ![]() is a
is a ![]() coefficient vector,
coefficient vector, ![]() is a
is a ![]() disturbance vector, and
disturbance vector, and ![]() is a sequence of independent normal error terms with mean 0 and variance
is a sequence of independent normal error terms with mean 0 and variance ![]() .
.
The generalized Durbin-Watson statistic is written as
where ![]() is a vector of OLS residuals and
is a vector of OLS residuals and ![]() is a
is a ![]() matrix. The generalized Durbin-Watson statistic DW
matrix. The generalized Durbin-Watson statistic DW![]() can be rewritten as
can be rewritten as
where ![]() .
.
The marginal probability for the Durbin-Watson statistic is
where ![]() .
.
The p-value or the marginal probability for the generalized Durbin-Watson statistic is computed by numerical inversion of the characteristic
function ![]() of the quadratic form
of the quadratic form ![]() . The trapezoidal rule approximation to the marginal probability
. The trapezoidal rule approximation to the marginal probability ![]() is
is
where ![]() is the imaginary part of the characteristic function,
is the imaginary part of the characteristic function, ![]() and
and ![]() are integration and truncation errors, respectively. Refer to Davies (1973) for numerical inversion of the characteristic function.
are integration and truncation errors, respectively. Refer to Davies (1973) for numerical inversion of the characteristic function.
Ansley, Kohn, and Shively (1992) proposed a numerically efficient algorithm that requires O(![]() ) operations for evaluation of the characteristic function
) operations for evaluation of the characteristic function ![]() . The characteristic function is denoted as
. The characteristic function is denoted as
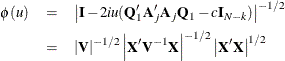
where ![]() and
and ![]() . By applying the Cholesky decomposition to the complex matrix
. By applying the Cholesky decomposition to the complex matrix ![]() , you can obtain the lower triangular matrix
, you can obtain the lower triangular matrix ![]() that satisfies
that satisfies ![]() . Therefore, the characteristic function can be evaluated in O(
. Therefore, the characteristic function can be evaluated in O(![]() ) operations by using the following formula:
) operations by using the following formula:
where ![]() . Refer to Ansley, Kohn, and Shively (1992) for more information on evaluation of the characteristic function.
. Refer to Ansley, Kohn, and Shively (1992) for more information on evaluation of the characteristic function.
When regressors contain lagged dependent variables, the Durbin-Watson statistic (![]() ) for the first-order autocorrelation is biased toward 2 and has reduced power. Wallis (1972) shows that the bias in the Durbin-Watson statistic (
) for the first-order autocorrelation is biased toward 2 and has reduced power. Wallis (1972) shows that the bias in the Durbin-Watson statistic (![]() ) for the fourth-order autocorrelation is smaller than the bias in
) for the fourth-order autocorrelation is smaller than the bias in ![]() in the presence of a first-order lagged dependent variable. Durbin (1970) proposes two alternative statistics (Durbin h and t ) that are asymptotically equivalent. The h statistic is written as
in the presence of a first-order lagged dependent variable. Durbin (1970) proposes two alternative statistics (Durbin h and t ) that are asymptotically equivalent. The h statistic is written as
where ![]() and
and ![]() is the least squares variance estimate for the coefficient of the lagged dependent variable. Durbin’s t test consists of regressing the OLS residuals
is the least squares variance estimate for the coefficient of the lagged dependent variable. Durbin’s t test consists of regressing the OLS residuals ![]() on explanatory variables and
on explanatory variables and ![]() and testing the significance of the estimate for coefficient of
and testing the significance of the estimate for coefficient of ![]() .
.
Inder (1984) shows that the Durbin-Watson test for the absence of first-order autocorrelation is generally more powerful than the h test in finite samples. Refer to Inder (1986) and King and Wu (1991) for the Durbin-Watson test in the presence of lagged dependent variables.
The GODFREY= option in the MODEL statement produces the Godfrey Lagrange multiplier test for serially correlated residuals for each equation (Godfrey, 1978b, 1978a). r is the maximum autoregressive order, and specifies that Godfrey’s tests be computed for lags 1 through r. The default number of lags is four.
Ramsey’s reset test is a misspecification test associated with the functional form of models to check whether power transforms need to be added to a model. The original linear model, henceforth called the restricted model, is
To test for misspecification in the functional form, the unrestricted model is
where ![]() is the predicted value from the linear model and p is the power of
is the predicted value from the linear model and p is the power of ![]() in the unrestricted model equation starting from 2. The number of higher-ordered terms to be chosen depends on the discretion
of the analyst. The RESET option produces test results for
in the unrestricted model equation starting from 2. The number of higher-ordered terms to be chosen depends on the discretion
of the analyst. The RESET option produces test results for ![]() 2, 3, and 4.
2, 3, and 4.
The reset test is an F statistic for testing ![]() , for all
, for all ![]() , against
, against ![]() for at least one
for at least one ![]() in the unrestricted model and is computed as follows:
in the unrestricted model and is computed as follows:
where ![]() is the sum of squared errors due to the restricted model,
is the sum of squared errors due to the restricted model, ![]() is the sum of squared errors due to the unrestricted model, n is the total number of observations, and k is the number of parameters in the original linear model.
is the sum of squared errors due to the unrestricted model, n is the total number of observations, and k is the number of parameters in the original linear model.
Ramsey’s test can be viewed as a linearity test that checks whether any nonlinear transformation of the specified independent variables has been omitted, but it need not help in identifying a new relevant variable other than those already specified in the current model.
For nonlinear time series models, the portmanteau test statistic based on squared residuals is used to test for independence of the series (McLeod and Li, 1983):
where
This Q statistic is used to test the nonlinear effects (for example, GARCH effects) present in the residuals. The GARCH![]() process can be considered as an ARMA
process can be considered as an ARMA![]() process. See the section Predicting the Conditional Variance. Therefore, the Q statistic calculated from the squared residuals can be used to identify the order of the GARCH process.
process. See the section Predicting the Conditional Variance. Therefore, the Q statistic calculated from the squared residuals can be used to identify the order of the GARCH process.
Engle (1982) proposed a Lagrange multiplier test for ARCH disturbances. The test statistic is asymptotically equivalent to the test used by Breusch and Pagan (1979). Engle’s Lagrange multiplier test for the qth order ARCH process is written
where
and
![\[ \mb{Z} = \begin{bmatrix} 1 & \hat{{\nu }}_{0}^{2} & {\cdots } & \hat{{\nu }}_{-q+1}^{2} \\ {\vdots } & {\vdots } & {\vdots } & {\vdots } \\ {\vdots } & {\vdots } & {\vdots } & {\vdots } \\ 1 & \hat{{\nu }}_{N-1}^{2} & {\cdots } & \hat{{\nu }}_{N-q}^{2} \end{bmatrix} \]](images/etsug_autoreg0724.png)
The presample values ( ![]() ,
,![]() ,
, ![]() ) have been set to 0. Note that the LM
) have been set to 0. Note that the LM![]() tests might have different finite-sample properties depending on the presample values, though they are asymptotically equivalent
regardless of the presample values.
tests might have different finite-sample properties depending on the presample values, though they are asymptotically equivalent
regardless of the presample values.
Engle’s Lagrange multiplier test for ARCH disturbances is a two-sided test; that is, it ignores the inequality constraints
for the coefficients in ARCH models. Lee and King (1993) propose a one-sided test and prove that the test is locally most mean powerful. Let ![]() , denote the residuals to be tested. Lee and King’s test checks
, denote the residuals to be tested. Lee and King’s test checks
where ![]() are in the following ARCH(q) model:
are in the following ARCH(q) model:
The statistic is written as
![\[ S=\frac{\sum _{t=q+1}^{T}{(\frac{\varepsilon _ t^2}{h_0}-1)\sum _{i=1}^{q}{\varepsilon _{t-i}^2}}}{\left[2\sum _{t=q+1}^{T}{(\sum _{i=1}^{q}{\varepsilon _{t-i}^2})^2}-\frac{2(\sum _{t=q+1}^{T} {\sum _{i=1}^{q}{\varepsilon _{t-i}^2}})^2}{T-q}\right]^{1/2}} \]](images/etsug_autoreg0733.png)
Wong and Li (1995) propose a rank portmanteau statistic to minimize the effect of the existence of outliers in the test for ARCH disturbances.
They first rank the squared residuals; that is, ![]() . Then they calculate the rank portmanteau statistic
. Then they calculate the rank portmanteau statistic
where ![]() ,
, ![]() , and
, and ![]() are defined as follows:
are defined as follows:
The Q, Engle’s LM, Lee and King’s, and Wong and Li’s statistics are computed from the OLS residuals, or residuals if the NLAG=
option is specified, assuming that disturbances are white noise. The Q, Engle’s LM, and Wong and Li’s statistics have an approximate
![]() distribution under the white-noise null hypothesis, while the Lee and King’s statistic has a standard normal distribution
under the white-noise null hypothesis.
distribution under the white-noise null hypothesis, while the Lee and King’s statistic has a standard normal distribution
under the white-noise null hypothesis.
Consider the linear regression model
where the parameter vector ![]() contains k elements.
contains k elements.
Split the observations for this model into two subsets at the break point specified by the CHOW= option, so that
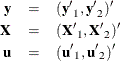
Now consider the two linear regressions for the two subsets of the data modeled separately,
where the number of observations from the first set is ![]() and the number of observations from the second set is
and the number of observations from the second set is ![]() .
.
The Chow test statistic is used to test the null hypothesis ![]() conditional on the same error variance
conditional on the same error variance ![]() . The Chow test is computed using three sums of square errors:
. The Chow test is computed using three sums of square errors:
where ![]() is the regression residual vector from the full set model,
is the regression residual vector from the full set model, ![]() is the regression residual vector from the first set model, and
is the regression residual vector from the first set model, and ![]() is the regression residual vector from the second set model. Under the null hypothesis, the Chow test statistic has an F distribution with
is the regression residual vector from the second set model. Under the null hypothesis, the Chow test statistic has an F distribution with ![]() and
and ![]() degrees of freedom, where
degrees of freedom, where ![]() is the number of elements in
is the number of elements in ![]() .
.
Chow (1960) suggested another test statistic that tests the hypothesis that the mean of prediction errors is 0. The predictive Chow
test can also be used when ![]() .
.
The PCHOW= option computes the predictive Chow test statistic
The predictive Chow test has an F distribution with ![]() and
and ![]() degrees of freedom.
degrees of freedom.
Bai and Perron (1998) propose several kinds of multiple structural change tests: (1) the test of no break versus a fixed number of breaks (![]() test), (2) the equal and unequal weighted versions of double maximum tests of no break versus an unknown number of breaks
given some upper bound (
test), (2) the equal and unequal weighted versions of double maximum tests of no break versus an unknown number of breaks
given some upper bound (![]() test and
test and ![]() test), and (3) the test of l versus
test), and (3) the test of l versus ![]() breaks (
breaks (![]() test). Bai and Perron (2003a, 2003b, 2006) also show how to implement these tests, the commonly used critical values, and the simulation analysis on these tests.
test). Bai and Perron (2003a, 2003b, 2006) also show how to implement these tests, the commonly used critical values, and the simulation analysis on these tests.
Consider the following partial structural change model with m breaks (![]() regimes):
regimes):
Here, ![]() is the dependent variable observed at time t,
is the dependent variable observed at time t, ![]() is a vector of covariates with coefficients
is a vector of covariates with coefficients ![]() unchanged over time, and
unchanged over time, and ![]() is a vector of covariates with coefficients
is a vector of covariates with coefficients ![]() at regime j,
at regime j, ![]() . If
. If ![]() (that is, there are no x regressors), the regression model becomes the pure structural change model. The indices
(that is, there are no x regressors), the regression model becomes the pure structural change model. The indices ![]() (that is, the break dates or break points) are unknown, and the convenient notation
(that is, the break dates or break points) are unknown, and the convenient notation ![]() and
and ![]() applies. For any given m-partition
applies. For any given m-partition ![]() , the associated least squares estimates of
, the associated least squares estimates of ![]() and
and ![]() are obtained by minimizing the sum of squared residuals (SSR),
are obtained by minimizing the sum of squared residuals (SSR),
Let ![]() denote the minimized SSR for a given
denote the minimized SSR for a given ![]() . The estimated break dates
. The estimated break dates ![]() are such that
are such that
where the minimization is taken over all partitions ![]() such that
such that ![]() . Bai and Perron (2003a) propose an efficient algorithm, based on the principle of dynamic programming, to estimate the preceding model.
. Bai and Perron (2003a) propose an efficient algorithm, based on the principle of dynamic programming, to estimate the preceding model.
In the case that the data are nontrending, as stated in Bai and Perron (1998), the limiting distribution of the break dates is as follows:
where
and
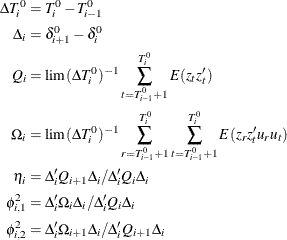
Also, ![]() and
and ![]() are independent standard Weiner processes that are defined on
are independent standard Weiner processes that are defined on ![]() , starting at the origin when
, starting at the origin when ![]() ; these processes are also independent across i. The cumulative distribution function of
; these processes are also independent across i. The cumulative distribution function of ![]() is shown in Bai (1997). Hence, with the estimates of
is shown in Bai (1997). Hence, with the estimates of ![]() ,
, ![]() , and
, and ![]() , the relevant critical values for confidence interval of break dates
, the relevant critical values for confidence interval of break dates ![]() can be calculated. The estimate of
can be calculated. The estimate of ![]() is
is ![]() . The estimate of
. The estimate of ![]() is either
is either
if the regressors are assumed to have heterogeneous distributions across regimes (that is, the HQ option is specified), or
if the regressors are assumed to have identical distributions across regimes (that is, the HQ option is not specified). The
estimate of ![]() can also be constructed with data over regime i only or the whole sample, depending on whether the vectors
can also be constructed with data over regime i only or the whole sample, depending on whether the vectors ![]() are heterogeneously distributed across regimes (that is, the HO option is specified). If the HAC option is specified,
are heterogeneously distributed across regimes (that is, the HO option is specified). If the HAC option is specified, ![]() is estimated through the heteroscedasticity- and autocorrelation-consistent (HAC) covariance matrix estimator applied to
vectors
is estimated through the heteroscedasticity- and autocorrelation-consistent (HAC) covariance matrix estimator applied to
vectors ![]() .
.
The ![]() test of no structural break
test of no structural break ![]() versus the alternative hypothesis that there are a fixed number,
versus the alternative hypothesis that there are a fixed number, ![]() , of breaks is defined as follows:
, of breaks is defined as follows:
where
![\[ R_{(kq)\times (p+(k+1)q)} = \left( \begin{array}{ ccccccc } 0_{q \times p} & I_ q & -I_ q & 0 & 0 & \cdots & 0 \\ 0_{q \times p} & 0 & I_ q & -I_ q & 0 & \cdots & 0 \\ \vdots & \cdots & \ddots & \ddots & \ddots & \ddots & \cdots \\ 0_{q \times p} & 0 & \cdots & \cdots & 0 & I_ q & -I_ q \end{array} \right) \]](images/etsug_autoreg0793.png)
and ![]() is the
is the ![]() identity matrix;
identity matrix; ![]() is the coefficient vector
is the coefficient vector ![]() , which together with the break dates
, which together with the break dates ![]() minimizes the global sum of squared residuals; and
minimizes the global sum of squared residuals; and ![]() is an estimate of the variance-covariance matrix of
is an estimate of the variance-covariance matrix of ![]() , which could be estimated by using the HAC estimator or another way, depending on how the HAC, HR, and HE options are specified.
The output
, which could be estimated by using the HAC estimator or another way, depending on how the HAC, HR, and HE options are specified.
The output ![]() test statistics are scaled by q, the number of regressors, to be consistent with the limiting distribution; Bai and Perron (2003b, 2006) take the same action.
test statistics are scaled by q, the number of regressors, to be consistent with the limiting distribution; Bai and Perron (2003b, 2006) take the same action.
There are two versions of double maximum tests of no break against an unknown number of breaks given some upper bound ![]() : the
: the ![]() test:
test:
and the ![]() test:
test:
where ![]() is the significance level and
is the significance level and ![]() is the critical value of
is the critical value of ![]() test given the significance level
test given the significance level ![]() . Four kinds of
. Four kinds of ![]() tests that correspond to
tests that correspond to ![]() , and 0.010 are implemented.
, and 0.010 are implemented.
The ![]() test of l versus
test of l versus ![]() breaks is calculated in two ways that are asymptotically the same. In the first calculation, the method amounts to the application
of
breaks is calculated in two ways that are asymptotically the same. In the first calculation, the method amounts to the application
of ![]() tests of the null hypothesis of no structural change versus the alternative hypothesis of a single change. The test is applied
to each segment that contains the observations
tests of the null hypothesis of no structural change versus the alternative hypothesis of a single change. The test is applied
to each segment that contains the observations ![]() to
to ![]()
![]() . The
. The ![]() test statistics are the maximum of these
test statistics are the maximum of these ![]()
![]() test statistics. In the second calculation, for the given l breaks
test statistics. In the second calculation, for the given l breaks ![]() , the new break
, the new break ![]() is to minimize the global SSR:
is to minimize the global SSR:
Then,
The p-value of each test is based on the simulation of the limiting distribution of that test.