The AUTOREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics
Missing ValuesAutoregressive Error ModelAlternative Autocorrelation Correction MethodsGARCH ModelsHeteroscedasticity- and Autocorrelation-Consistent Covariance Matrix EstimatorGoodness-of-Fit Measures and Information CriteriaTestingPredicted ValuesOUT= Data SetOUTEST= Data SetPrinted OutputODS Table NamesODS Graphics -
Examples

- References
Consider the series ![]() , which follows the GARCH process. The conditional distribution of the series Y for time t is written
, which follows the GARCH process. The conditional distribution of the series Y for time t is written
where ![]() denotes all available information at time
denotes all available information at time ![]() . The conditional variance
. The conditional variance ![]() is
is
where
The GARCH![]() model reduces to the ARCH
model reduces to the ARCH![]() process when
process when ![]() . At least one of the ARCH parameters must be nonzero (
. At least one of the ARCH parameters must be nonzero (![]() ). The GARCH regression model can be written
). The GARCH regression model can be written
where ![]() .
.
In addition, you can consider the model with disturbances following an autoregressive process and with the GARCH errors. The
AR![]() -GARCH
-GARCH![]() regression model is denoted
regression model is denoted
The GARCH![]() model is written in ARCH(
model is written in ARCH(![]() ) form as
) form as
![\begin{eqnarray*} h_{t} & =& \left( 1-\sum _{j=1}^ p {\gamma }_{j}{B} ^{j} \right)^{-1} \left[{{\omega } + \sum _{i=1}^{q}{{\alpha }_{i} {\epsilon }_{t-i}^{2}}}\right] \nonumber \\ & =& {\omega }^{*} + \sum _{i=1}^{{\infty }}{{\phi }_{i} {\epsilon }_{t-i}^{2}} \end{eqnarray*}](images/etsug_autoreg0234.png)
where B is a backshift operator. Therefore, ![]() if
if ![]() and
and ![]() . Assume that the roots of the following polynomial equation are inside the unit circle:
. Assume that the roots of the following polynomial equation are inside the unit circle:
where ![]() and Z is a complex scalar.
and Z is a complex scalar. ![]() and
and ![]() do not share common factors. Under these conditions,
do not share common factors. Under these conditions, ![]() ,
, ![]() , and these coefficients of the ARCH(
, and these coefficients of the ARCH(![]() ) process are well defined.
) process are well defined.
Define ![]() . The coefficient
. The coefficient ![]() is written
is written
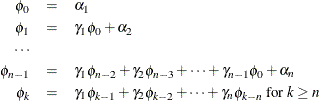
where ![]() for
for ![]() and
and ![]() for
for ![]() .
.
Nelson and Cao (1992) proposed the finite inequality constraints for GARCH![]() and GARCH
and GARCH![]() cases. However, it is not straightforward to derive the finite inequality constraints for the general GARCH
cases. However, it is not straightforward to derive the finite inequality constraints for the general GARCH![]() model.
model.
For the GARCH![]() model, the nonlinear inequality constraints are
model, the nonlinear inequality constraints are
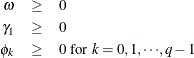
For the GARCH![]() model, the nonlinear inequality constraints are
model, the nonlinear inequality constraints are
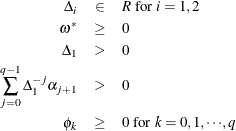
where ![]() and
and ![]() are the roots of
are the roots of ![]() .
.
For the GARCH![]() model with
model with ![]() , only
, only ![]() nonlinear inequality constraints (
nonlinear inequality constraints (![]() for
for ![]() to max(
to max(![]() )) are imposed, together with the in-sample positivity constraints of the conditional variance
)) are imposed, together with the in-sample positivity constraints of the conditional variance ![]() .
.
The HETERO statement can be combined with the GARCH= option in the MODEL statement to include input variables in the GARCH
conditional variance model. For example, the GARCH![]() variance model with two dummy input variables D1 and D2 is
variance model with two dummy input variables D1 and D2 is
The following statements estimate this GARCH model:
proc autoreg data=one; model y = x z / garch=(p=1,q=1); hetero d1 d2; run;
The parameters for the variables D1 and D2 can be constrained using the COEF= option. For example, the constraints ![]() are imposed by the following statements:
are imposed by the following statements:
proc autoreg data=one; model y = x z / garch=(p=1,q=1); hetero d1 d2 / coef=unit; run;
The condition ![]() implies that the GARCH process is weakly stationary since the mean, variance, and autocovariance are finite and constant
over time. When the GARCH process is stationary, the unconditional variance of
implies that the GARCH process is weakly stationary since the mean, variance, and autocovariance are finite and constant
over time. When the GARCH process is stationary, the unconditional variance of ![]() is computed as
is computed as
where ![]() and
and ![]() is the GARCH
is the GARCH![]() conditional variance.
conditional variance.
Sometimes the multistep forecasts of the variance do not approach the unconditional variance when the model is integrated
in variance; that is, ![]() .
.
The unconditional variance for the IGARCH model does not exist. However, it is interesting that the IGARCH model can be strongly stationary even though it is not weakly stationary. Refer to Nelson (1990) for details.
The EGARCH model was proposed by Nelson (1991). Nelson and Cao (1992) argue that the nonnegativity constraints in the linear GARCH model are too restrictive. The GARCH model imposes the nonnegative
constraints on the parameters, ![]() and
and ![]() , while there are no restrictions on these parameters in the EGARCH model. In the EGARCH model, the conditional variance,
, while there are no restrictions on these parameters in the EGARCH model. In the EGARCH model, the conditional variance,
![]() , is an asymmetric function of lagged disturbances
, is an asymmetric function of lagged disturbances ![]() :
:
where
The coefficient of the second term in ![]() is set to be 1 (
is set to be 1 (![]() =1) in our formulation. Note that
=1) in our formulation. Note that ![]() if
if ![]() . The properties of the EGARCH model are summarized as follows:
. The properties of the EGARCH model are summarized as follows:
-
The function
 is linear in
is linear in  with slope coefficient
with slope coefficient 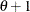 if
if  is positive while
is positive while 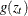 is linear in
is linear in  with slope coefficient
with slope coefficient 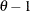 if
if  is negative.
is negative.
-
Suppose that
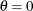 . Large innovations increase the conditional variance if
. Large innovations increase the conditional variance if 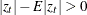 and decrease the conditional variance if
and decrease the conditional variance if 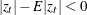 .
.
-
Suppose that
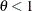 . The innovation in variance,
. The innovation in variance, 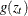 , is positive if the innovations
, is positive if the innovations  are less than
are less than 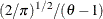 . Therefore, the negative innovations in returns,
. Therefore, the negative innovations in returns, 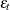 , cause the innovation to the conditional variance to be positive if
, cause the innovation to the conditional variance to be positive if 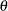 is much less than 1.
is much less than 1.
As shown in many empirical studies, positive and negative innovations have different impacts on future volatility. There is a long list of variations of GARCH models that consider the asymmetricity. Three typical variations are the quadratic GARCH (QGARCH) model (Engle and Ng, 1993), the threshold GARCH (TGARCH) model (Glosten, Jaganathan, and Runkle, 1993; Zakoian, 1994), and the power GARCH (PGARCH) model (Ding, Granger, and Engle, 1993). For more details about the asymmetric GARCH models, see Engle and Ng (1993).
In the QGARCH model, the lagged errors’ centers are shifted from zero to some constant values:
In the TGARCH model, there is an extra slope coefficient for each lagged squared error,
where the indicator function ![]() is one if
is one if ![]() ; otherwise, zero.
; otherwise, zero.
The PGARCH model not only considers the asymmetric effect, but also provides another way to model the long memory property in the volatility,
where ![]() and
and ![]() .
.
Note that the implemented TGARCH model is also well known as GJR-GARCH (Glosten, Jaganathan, and Runkle, 1993), which is similar to the threshold GARCH model proposed by Zakoian (1994) but not exactly same. In Zakoian’s model, the conditional standard deviation is a linear function of the past values of
the white noise. Zakoian’s version can be regarded as a special case of PGARCH model when ![]() .
.
The GARCH-M model has the added regressor that is the conditional standard deviation:
where ![]() follows the ARCH or GARCH process.
follows the ARCH or GARCH process.
The family of GARCH models are estimated using the maximum likelihood method. The log-likelihood function is computed from the product of all conditional densities of the prediction errors.
When ![]() is assumed to have a standard normal distribution (
is assumed to have a standard normal distribution (![]() ), the log-likelihood function is given by
), the log-likelihood function is given by
where ![]() and
and ![]() is the conditional variance. When the GARCH
is the conditional variance. When the GARCH![]() -M model is estimated,
-M model is estimated, ![]() . When there are no regressors, the residuals
. When there are no regressors, the residuals ![]() are denoted as
are denoted as ![]() or
or ![]() .
.
If ![]() has the standardized Student’s t distribution, the log-likelihood function for the conditional t distribution is
has the standardized Student’s t distribution, the log-likelihood function for the conditional t distribution is
where ![]() is the gamma function and
is the gamma function and ![]() is the degree of freedom (
is the degree of freedom (![]() ). Under the conditional t distribution, the additional parameter
). Under the conditional t distribution, the additional parameter ![]() is estimated. The log-likelihood function for the conditional t distribution converges to the log-likelihood function of the conditional normal GARCH model as
is estimated. The log-likelihood function for the conditional t distribution converges to the log-likelihood function of the conditional normal GARCH model as ![]() .
.
The likelihood function is maximized via either the dual quasi-Newton or the trust region algorithm. The default is the dual
quasi-Newton algorithm. The starting values for the regression parameters ![]() are obtained from the OLS estimates. When there are autoregressive parameters in the model, the initial values are obtained
from the Yule-Walker estimates. The starting value
are obtained from the OLS estimates. When there are autoregressive parameters in the model, the initial values are obtained
from the Yule-Walker estimates. The starting value ![]() is used for the GARCH process parameters.
is used for the GARCH process parameters.
The variance-covariance matrix is computed using the Hessian matrix. The dual quasi-Newton method approximates the Hessian
matrix while the quasi-Newton method gets an approximation of the inverse of Hessian. The trust region method uses the Hessian matrix obtained
using numerical differentiation. When there are active constraints, that is, ![]() , the variance-covariance matrix is given by
, the variance-covariance matrix is given by
where ![]() and
and ![]() . Therefore, the variance-covariance matrix without active constraints reduces to
. Therefore, the variance-covariance matrix without active constraints reduces to ![]() .
.