The ARIMA Procedure

Example 7.1 Simulated IMA Model

This example illustrates the ARIMA procedure results for a case where the true model is known. An integrated moving-average model is used for this illustration.

The following DATA step generates a pseudo-random sample of 100 periods from the ARIMA(0,1,1) process ${u_{t} = u_{t-1} + a_{t} - 0.8a_{t-1}}$, ${a_{t}~ \mr{iid ~ N} (0,1)}$: 

title1 'Simulated IMA(1,1) Series';
data a;
  u1 = 0.9; a1 = 0;
  do i = -50 to 100;
     a = rannor( 32565 );
     u = u1 + a - .8 * a1;
     if i > 0 then output;
     a1 = a;
     u1 = u;
  end;
run;

The following ARIMA procedure statements identify and estimate the model: 

/*-- Simulated IMA Model --*/
proc arima data=a;
  identify var=u;
  run;
  identify var=u(1);
  run;
  estimate q=1 ;
  run;
quit;

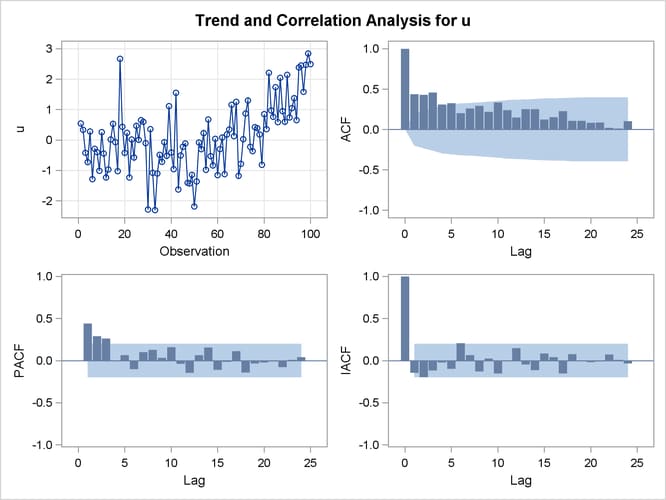
The graphical series correlation analysis output of the first IDENTIFY statement is shown in Output 7.1.1. The output shows the behavior of the sample autocorrelation function when the process is nonstationary. Note that in this case the estimated autocorrelations are not very high, even at small lags. Nonstationarity is reflected in a pattern of significant autocorrelations that do not decline quickly with increasing lag, not in the size of the autocorrelations.

Output 7.1.1: Correlation Analysis from the First IDENTIFY Statement

Correlation Analysis from the First IDENTIFY Statement


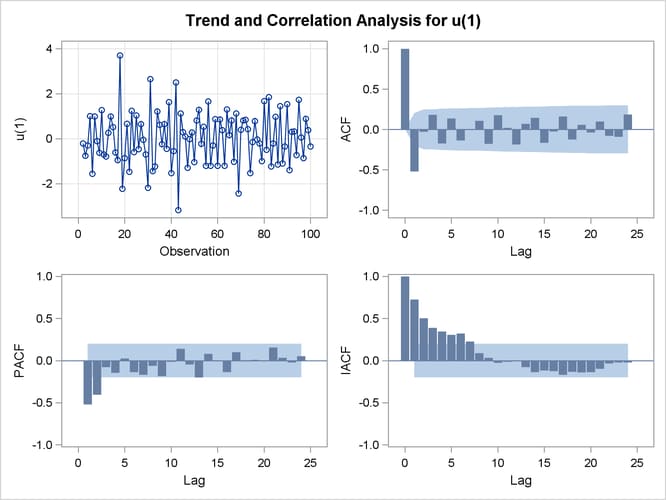
The second IDENTIFY statement differences the series. The results of the second IDENTIFY statement are shown in Output 7.1.2. This output shows autocorrelation, inverse autocorrelation, and partial autocorrelation functions typical of MA(1) processes.

Output 7.1.2: Correlation Analysis from the Second IDENTIFY Statement

Correlation Analysis from the Second IDENTIFY Statement


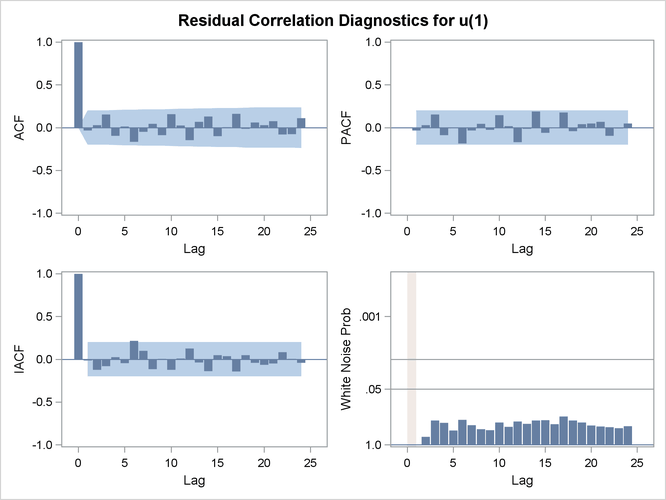
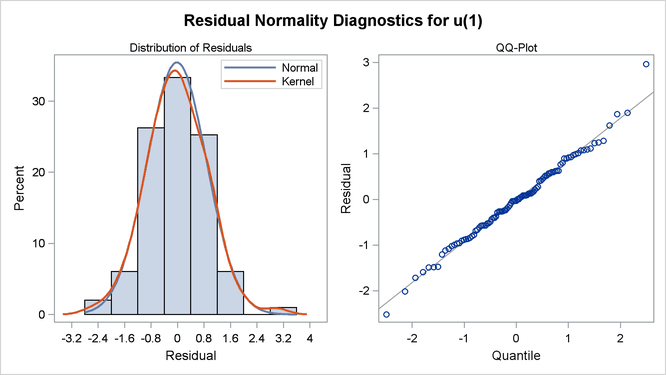
The ESTIMATE statement fits an ARIMA(0,1,1) model to the simulated data. Note that in this case the parameter estimates are reasonably close to the values used to generate the simulated data. (${{\mu }=0,~ \hat{{\mu }}=0.02;~ ~ {\theta }_{1}=0.8,~ \hat{{\theta }}_{1}=0.79;~ ~ {\sigma }^{2}=1,~ \hat{{\sigma }}^{2}=0.82.}$) Moreover, the graphical analysis of the residuals shows no model inadequacies (see Output 7.1.4 and Output 7.1.5).

The ESTIMATE statement results are shown in Output 7.1.3.

Output 7.1.3: Output from Fitting ARIMA(0,1,1) Model

Conditional Least Squares Estimation
Parameter Estimate Standard
Error 		t Value Approx
Pr > |t| 		Lag
MU 0.02056 0.01972 1.04 0.2997 0
MA1,1 0.79142 0.06474 12.22 <.0001 1

Constant Estimate 0.020558
Variance Estimate 0.819807
Std Error Estimate 0.905432
AIC 263.2594
SBC 268.4497
Number of Residuals 99

Model for variable u
Estimated Mean 0.020558
Period(s) of Differencing 1

Moving Average Factors
Factor 1: 1 - 0.79142 B**(1) 




            

            


            
  

            


Output 7.1.4: Residual Correlation Analysis of the ARIMA(0,1,1) Model

               

                  
Residual Correlation Analysis of the ARIMA(0,1,1) Model

               

            

            


            


Output 7.1.5: Residual Normality Analysis of the ARIMA(0,1,1) Model

               

                  
Residual Normality Analysis of the ARIMA(0,1,1) Model