Panel Data Analysis :: SAS/ETS(R) 12.3 User's Guide

Panel Data Poisson Regression with Fixed Effects

The count regression model for panel data can be derived from the Poisson regression model. Consider the multiplicative one-way panel data model,

$y_{it} \sim \mbox{Poisson}(\mu _{it})$

where

$\mu _{it} = \alpha _{i} \lambda _{it} = \alpha _{i} \exp (\mathbf{x}_{it}’\bbeta ),\; \; i=1,\ldots ,N, \; \; t=1,\ldots ,T$

Here, $\alpha _{i}$ are the individual effects.

In the fixed effects model, the $\alpha _{i}$ are unknown parameters. The fixed effects model can be estimated by eliminating $\alpha _{i}$ by conditioning on $\sum _{t} y_{it}$ .

In the random effects model, the $\alpha _{i}$ are independent and identically distributed (iid) random variables, in contrast to the fixed effects model. The random effects model can then be estimated by assuming a distribution for $\alpha _{i}$ .

In the Poisson fixed effects model, conditional on $\lambda _{it}$ and parameter $\alpha _{i}$ , $y_{it}$ is iid Poisson distributed with parameter $\mu _{it}=\alpha _{i}\lambda _{it}=\alpha _{i} \exp (\mathbf{x}_{it}’\bbeta )$ , and $x_{it}$ does not include an intercept. Then, the conditional joint density for the outcomes within the th panel is

$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\sum _{t=1}^{T_{i}}y_{it}]$	$\displaystyle =$	$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}},\sum _{t=1}^{T_{i}}y_{it}] / P[\sum _{t=1}^{T_{i}}y_{it}]$
$\displaystyle$	$\displaystyle =$	$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}]/P[\sum _{t=1}^{T_{i}}y_{it}]$

Since $y_{it}$ is iid Poisson( $\mu _{it}$ ), $P[y_{i1},\ldots ,y_{iT_{i}}]$ is the product of $T_{i}$ Poisson densities. Also, $(\sum _{t=1}^{T_{i}} y_{it})$ is Poisson( $\sum _{t=1}^{T_{i}} \mu _{it}$ ). Then,

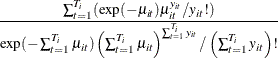$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\sum _{t=1}^{T_{i}}y_{it}]$	$\displaystyle =$	$\displaystyle \frac{\sum _{t=1}^{T_{i}} (\exp (-\mu _{it}) \mu _{it}^{y_{it}} / y_{it}! )}{\exp (-\sum _{t=1}^{T_{i}} \mu _{it}) \left( \sum _{t=1}^{T_{i}} \mu _{it} \right)^{\sum _{t=1}^{T_{i}} y_{it} } / \left( \sum _{t=1}^{T_{i}} y_{it} \right)!}$
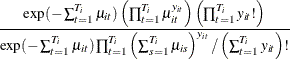$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{\exp (-\sum _{t=1}^{T_{i}} \mu _{it}) \left( \prod _{t=1}^{T_{i}} \mu _{it}^{y_{it}} \right) \left( \prod _{t=1}^{T_{i}} y_{it}! \right) }{\exp ( -\sum _{t=1}^{T_{i}} \mu _{it}) \prod _{t=1}^{T_{i}} \left( \sum _{s=1}^{T_{i}} \mu _{is} \right)^{y_{it}} / \left( \sum _{t=1}^{T_{i}} y_{it} \right)!}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{(\sum _{t=1}^{T_{i}} y_{it})!}{(\prod _{t=1}^{T_{i}} y_{it}!)} \prod _{t=1}^{T_{i}} \left(\frac{\mu _{it}}{\sum _{s=1}^{T_{i}} \mu _{is}}\right)^{y_{it}}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{(\sum _{t=1}^{T_{i}} y_{it})!}{(\prod _{t=1}^{T_{i}} y_{it}!)} \prod _{t=1}^{T_{i}} \left(\frac{\lambda _{it}}{\sum _{s=1}^{T_{i}} \lambda _{is}}\right)^{y_{it}}$

Thus, the conditional log-likelihood function of the fixed effects Poisson model is given by

$\mathcal{L} = \sum _{i=1}^{N} \left[ \ln \left( (\sum _{t=1}^{T_{i}}y_{it})! \right) - \sum _{t=1}^{T_{i}}\ln (y_{it}!) + \sum _{t=1}^{T_{i}}y_{it}\ln \left(\frac{\lambda _{it}}{\sum _{s=1}^{T_{i}}\lambda _{is}}\right) \right]$

The gradient is

$\displaystyle \frac{\partial \mathcal{L}}{\partial \bbeta }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} y_{it}x_{it} - \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} \left[ \frac{y_{it} \sum _{s=1}^{T_{i}} \left( \exp (\mathbf{x}_{is}\bbeta ) \mathbf{x}_{is} \right)}{\sum _{s=1}^{T_{i}} \exp (\mathbf{x}_{is}\bbeta )} \right]$
$\displaystyle$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \sum _{t=1}^{T_{i}} y_{it} (\mathbf{x}_{it}-\mathbf{\bar{x}}_{i})$

where

$\mathbf{\bar{x}}_{i} = \sum _{s=1}^{T_{i}} \left( \frac{\exp (\mathbf{x}_{is}\bbeta )}{\sum _{k=1}^{T_{i}} \exp (\mathbf{x}_{ik}\bbeta )} \right) \mathbf{x}_{is}$

Panel Data Poisson Regression with Random Effects

In the Poisson random effects model, conditional on $\lambda _{it}$ and parameter $\alpha _{i}$ , $y_{it}$ is iid Poisson distributed with parameter $\mu _{it}=\alpha _{i}\lambda _{it}=\alpha _{i} \exp (\mathbf{x}_{it}’\bbeta )$ , and the individual effects, $\alpha _{i}$ , are assumed to be iid random variables. The joint density for observations in all time periods for the th individual, $P[y_{i1},\ldots ,y_{iT}|\lambda _{i1},\ldots ,\lambda _{iT_{i}}]$ , can be obtained after the density $g(\alpha )$ of $\alpha {_ i}$ is specified.

Let

$\alpha _{i} \sim \mbox{iid}\; \mathrm{gamma}(\theta ,\theta )$

so that $E(\alpha _{i})=1$ and $V(\alpha _{i}) = 1/\theta$ :

$g(\alpha _{i}) = \frac{\theta ^{\theta }}{\Gamma (\theta )} \alpha _{i}^{\theta -1}\exp (-\theta \alpha _{i})$

Let $\lambda _{i} = (\lambda _{i1},\ldots ,\lambda _{iT_{i}})$ . Since $y_{it}$ is conditional on $\lambda _{it}$ and parameter $\alpha _{i}$ is iid Poisson( $\mu _{it}=\alpha _{i} \lambda _{it}$ ), the conditional joint probability for observations in all time periods for the th individual, $P[y_{i1},\ldots ,y_{iT_{i}}|\lambda _{i},\alpha _{i}]$ , is the product of $T_{i}$ Poisson densities:

$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\lambda _{i},\alpha _{i}]$	$\displaystyle =$	$\displaystyle \prod _{t=1}^{T_{i}} P[y_{it}\| \lambda _{i}, \alpha _{i}]$
$\displaystyle$	$\displaystyle =$	$\displaystyle \prod _{t=1}^{T_{i}}\left[ \frac{\exp (-\mu _{it}) \mu _{it}^{y_{it}}}{y_{it}!} \right]$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[ \prod _{t=1}^{T_{i}} \frac{e^{-\alpha _{i}\lambda _{it}}(\alpha _{i}\lambda _{it})^{y_{it}}}{y_{it}!} \right]$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[ \prod _{t=1}^{T_{i}} \lambda _{it}^{y_{it}}/y_{it}! \right] \left( e^{-\alpha _{i} \sum _{t} \lambda _{it}} \alpha _{i}^{\sum _{t} y_{it}} \right)$

Then, the joint density for the th panel conditional on just the $\lambda$ can be obtained by integrating out $\alpha _{i}$ :

$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\lambda _{i}]$	$\displaystyle =$	$\displaystyle \int _{0}^{\infty } P[y_{i1},\ldots ,y_{iT}\|\lambda _{i},\alpha _{i}] g(\alpha _{i}) d\alpha _{i}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{\theta ^{\theta }}{\Gamma (\theta )} \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \int _{0}^{\infty } \exp (-\alpha _{i} \sum _{t} \lambda _{it}) \alpha _{i}^{\sum _{t} y_{it}} \alpha _{i}^{\theta -1} \exp (-\theta \alpha _{i}) d\alpha _{i}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{\theta ^{\theta }}{\Gamma (\theta )} \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \int _{0}^{\infty } \exp \left[ -\alpha _{i} \left( \theta + \sum _{t} \lambda _{it} \right) \right] \alpha _{i}^{\theta + \sum _{t} y_{it}-1} d\alpha _{i}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \frac{\Gamma (\theta + \sum _{t} y_{it})}{\Gamma (\theta )}$
$\displaystyle$	$\displaystyle$	$\displaystyle \times \left(\frac{\theta }{\theta +\sum _{t} \lambda _{it}} \right)^{\theta } \left(\theta + \sum _{t} \lambda _{it} \right)^{-\sum _{t} y_{it}}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \left[ \prod _{t=1}^{T_{i}} \frac{\lambda _{it}^{y_{it}}}{y_{it}!} \right] \frac{\Gamma (\alpha ^{-1}+ \sum _{t} y_{it})}{\Gamma (\alpha ^{-1})}$
$\displaystyle$	$\displaystyle$	$\displaystyle \times \left(\frac{\alpha ^{-1}}{\alpha ^{-1}+\sum _{t} \lambda _{it}} \right)^{\alpha ^{-1}} \left(\alpha ^{-1} + \sum _{t} \lambda _{it} \right)^{-\sum _{t} y_{it}}$

where $\alpha (=1/\theta )$ is the overdispersion parameter. This is the density of the Poisson random effects model with gamma-distributed random effects. For this distribution, $E(y_{it})=\lambda _{it}$ and $V(y_{it})=\lambda _{it} +\alpha \lambda _{it}^{2}$ ; that is, there is overdispersion.

Then the log-likelihood function is written as

$\displaystyle \mathcal{L}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \left\{ \sum _{t=1}^{T_{i}} \ln (\frac{\lambda _{it}^{y_{it}}}{y_{it}!}) + \alpha ^{-1} \ln (\alpha ^{-1}) -\alpha ^{-1} \ln (\alpha ^{-1}+\sum _{t=1}^{T_{i}}\lambda _{it}) \right\} +$
$\displaystyle$	$\displaystyle$	$\displaystyle \sum _{i=1}^{N} \left\{ - \left( \sum _{t=1}^{T_{i}}y_{it} \right) \ln \left(\alpha ^{-1}+\sum _{t=1}^{T_{i}}\lambda _{it}\right) + \right.$
$\displaystyle$	$\displaystyle$	$\displaystyle \left. \hspace*{0.3in} \ln \left[\Gamma \left(\alpha ^{-1}+ \sum _{t=1}^{T_{i}}y_{it} \right)\right] -\ln (\Gamma (\alpha ^{-1})) \right\}$

The gradient is

$\displaystyle \frac{\partial \mathcal{L}}{\partial \bbeta }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \left\{ \sum _{t=1}^{T_{i}} y_{it}\mathbf{x}_{it} - \frac{\alpha ^{-1}\sum _{t=1}^{T_{i}} \lambda _{it} \mathbf{x}_{it}}{\alpha ^{-1}+\sum _{t=1}^{T_{i}} \lambda _{it}}\right\} -$
$\displaystyle$	$\displaystyle$	$\displaystyle \sum _{i=1}^{N} \left\{ \left( \sum _{t=1}^{T_{i}} y_{it} \right) \frac{\sum _{t=1}^{T_{i}} \lambda _{it} \mathbf{x}_{it}}{\alpha ^{-1}+\sum _{t=1}^{T_{i}} \lambda _{it}} \right\}$
$\displaystyle \frac{\partial \mathcal{L}}{\partial \bbeta }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \left\{ \sum _{t=1}^{T_{i}} y_{it}\mathbf{x}_{it} - \frac{(\alpha ^{-1}+\sum _{t=1}^{T_{i}} y_{it}) (\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it})}{\alpha ^{-1}+\sum _{t=1}^{T_{i}} \lambda _{it}} \right\}$

and

$\displaystyle \frac{\partial \mathcal{L}}{\partial \alpha }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N} \left\{ -\alpha ^{-2} \left[ [1+ \ln (\alpha ^{-1})] - \frac{(\alpha ^{-1}+\sum _{t=1}^{T_{i}} y_{it})}{(\alpha ^{-1})+ \sum _{t=1}^{T_{i}}\lambda _{it}} - \ln \left(\alpha ^{-1} + \sum _{t=1}^{T_{i}} \lambda _{it} \right) \right] \right\}$
$\displaystyle$	$\displaystyle +$	$\displaystyle \sum _{i=1}^{N} \left\{ -\alpha ^{-2} \left[ \frac{\Gamma (\alpha ^{-1}+ \sum _{t=1}^{T_{i}} y_{it})}{\Gamma (\alpha ^{-1} +\sum _{t=1}^{T_{i}} y_{it})} -\frac{\Gamma (\alpha ^{-1})}{\Gamma (\alpha ^{-1})} \right] \right\}$

where $\lambda _{it} = \exp (\mathbf{x}_{it}’\bbeta )$ , $\Gamma ’(\cdot ) = d \Gamma (\cdot )/d (\cdot )$ and $\Gamma ’(\cdot )/\Gamma (\cdot )$ is the digamma function.

Panel Data Negative Binomial Regression with Fixed Effects

This section shows the derivation of a negative binomial model with fixed effects. Keep the assumptions of the Poisson-distributed dependent variable

$y_{it}\sim Poisson\left(\mu _{it}\right)$

But now let the Poisson parameter be random with gamma distribution and parameters $\left(\lambda _{it},\delta \right)$ ,

$\mu _{it}\sim \Gamma \left(\lambda _{it},\delta \right)$

where one of the parameters is the exponentially affine function of independent variables $\lambda _{it}=\exp \left(\mathbf{x}_{it}’\beta \right)$ . Use integration by parts to obtain the distribution of $y_{it}$ ,

$\displaystyle P\left[y_{it}\right]$	$\displaystyle =$	$\displaystyle \int _{0}^{\infty }\frac{e^{-\mu _{it}}\mu _{it}^{y_{it}}}{y_{it}!}f\left(\mu _{it}\right)d\mu _{it}$
$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\left(\frac{\delta }{1+\delta }\right)^{\lambda _{it}}\left(\frac{1}{1+\delta }\right)^{y_{it}}$

which is a negative binomial distribution with parameters $\left(\lambda _{it},\delta \right)$ . Conditional joint distribution is given as

$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\sum _{t=1}^{T_{i}}y_{it}]$	$\displaystyle =$	$\displaystyle \left(\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\right)$
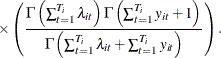$\displaystyle$	$\displaystyle$	$\displaystyle \times \left(\frac{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)\Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right).$

Hence, the conditional fixed-effects negative binomial log-likelihood is

$\displaystyle \mathcal{L}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\log \Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)+\log \Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)-\log \Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\log \Gamma \left(\lambda _{it}+y_{it}\right)-\log \Gamma \left(\lambda _{it}\right)-\log \Gamma \left(y_{it}+1\right)\right].$

The gradient is

$\displaystyle \frac{\partial \mathcal{L}}{\partial \beta }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\left(\frac{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}\right)}-\frac{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right)\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}\right]$
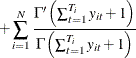$\displaystyle$	$\displaystyle$	$\displaystyle +\sum _{i=1}^{N}\frac{\Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)}{\Gamma \left(\sum _{t=1}^{T_{i}}y_{it}+1\right)}$
$\displaystyle$	$\displaystyle$	$\displaystyle +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\left(\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}+y_{it}\right)}-\frac{\Gamma \left(\lambda _{it}\right)}{\Gamma \left(\lambda _{it}\right)}\right)\lambda _{it}\mathbf{x}_{it}-\frac{\Gamma \left(y_{it}+1\right)}{\Gamma \left(y_{it}+1\right)}\right].$

Panel Data Negative Binomial Regression with Random Effects

This section describes the derivation of negative binomial model with random effects. Suppose

$y_{it}\sim Poisson\left(\mu _{it}\right)$

with the Poisson parameter distributed as gamma,

$\mu _{it}\sim \Gamma \left(\nu _{i}\lambda _{it},\delta \right)$

where its parameters are also random:

$\nu _{i}\lambda _{it}=\exp \left(\mathbf{x}_{it}’\beta +\eta _{it}\right)$

Assume that the distribution of a function of $\nu _{i}$ is beta with parameters $\left(a,b\right)$ :

$\frac{\nu _{i}}{1+\nu _{i}}\sim Beta\left(a,b\right).$

Explicitly, the beta density with $\left[0,1\right]$ domain is

$f\left(z\right)=\left[B\left(a,b\right)\right]^{-1}z^{a-1}\left(1-z\right)^{b-1}$

where $B\left(a,b\right)$ is the beta function. Then, conditional joint distribution of dependent variables is

$P[y_{i1},\ldots ,y_{iT_{i}}|\mathbf{x}_{i1},\ldots ,\mathbf{x}_{iT_{i}},\nu _{i}]=\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}\left(\frac{1}{1+\nu _{i}}\right)^{\lambda _{it}}\left(\frac{\nu _{i}}{1+\nu _{i}}\right)^{y_{it}}$

Integrating out the variable $\nu _{i}$ yields the following conditional distribution function:

$\displaystyle P[y_{i1},\ldots ,y_{iT_{i}}\|\mathbf{x}_{i1},\ldots ,\mathbf{x}_{iT_{i}}]$	$\displaystyle =$	$\displaystyle \int _{0}^{1}\left[\prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}z_{i}^{\lambda _{it}}\left(1-z_{i}\right)^{y_{it}}\right]f\left(z_{i}\right)dz_{i}$
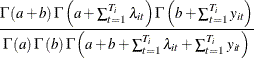$\displaystyle$	$\displaystyle =$	$\displaystyle \frac{\Gamma \left(a+b\right)\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a\right)\Gamma \left(b\right)\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}$
$\displaystyle$	$\displaystyle$	$\displaystyle \times \prod _{t=1}^{T_{i}}\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}\right)\Gamma \left(y_{it}+1\right)}.$

Consequently, the conditional log-likelihood function for a negative binomial model with random effects is

$\displaystyle \mathcal{L}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\log \Gamma \left(a+b\right)+\log \Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)+\log \Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle -\sum _{i=1}^{N}\left[\log \Gamma \left(a\right)+\log \Gamma \left(b\right)+\log \Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\log \Gamma \left(\lambda _{it}+y_{it}\right)-\log \Gamma \left(\lambda _{it}\right)-\log \Gamma \left(y_{it}+1\right)\right].$

The gradient is

$\displaystyle \frac{\partial \mathcal{L}}{\partial \beta }$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\frac{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}+\frac{\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle -\sum _{i=1}^{N}\left[\frac{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\sum _{t=1}^{T_{i}}\lambda _{it}\mathbf{x}_{it}\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle +\sum _{i=1}^{N}\sum _{t=1}^{T_{i}}\left[\left(\frac{\Gamma \left(\lambda _{it}+y_{it}\right)}{\Gamma \left(\lambda _{it}+y_{it}\right)}-\frac{\Gamma \left(\lambda _{it}\right)}{\Gamma \left(\lambda _{it}\right)}\right)\lambda _{it}\mathbf{x}_{it}-\frac{\Gamma \left(y_{it}+1\right)}{\Gamma \left(y_{it}+1\right)}\right],$

and

$\displaystyle \frac{\partial \mathcal{L}}{\partial a}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\frac{\Gamma \left(a+b\right)}{\Gamma \left(a+b\right)}+\frac{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}{\Gamma \left(a+\sum _{t=1}^{T_{i}}\lambda _{it}\right)}\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle -\sum _{i=1}^{N}\left[\frac{\Gamma \left(a\right)}{\Gamma \left(a\right)}+\frac{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right],$

and

$\displaystyle \frac{\partial \mathcal{L}}{\partial b}$	$\displaystyle =$	$\displaystyle \sum _{i=1}^{N}\left[\frac{\Gamma \left(a+b\right)}{\Gamma \left(a+b\right)}+\frac{\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(b+\sum _{t=1}^{T_{i}}y_{it}\right)}\right]$
$\displaystyle$	$\displaystyle$	$\displaystyle -\sum _{i=1}^{N}\left[\frac{\Gamma \left(b\right)}{\Gamma \left(b\right)}+\frac{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}{\Gamma \left(a+b+\sum _{t=1}^{T_{i}}\lambda _{it}+\sum _{t=1}^{T_{i}}y_{it}\right)}\right].$

The TCOUNTREG Procedure (Experimental)