Variable Selection :: SAS/ETS(R) 12.3 User's Guide

Variable Selection Using an Information Criterion

This type of variable selection uses either Akaike’s information criterion (AIC) or the Schwartz Bayesian criterion (SBC) and either a forward selection method or a backward elimination method.

Forward selection starts from a small subset of variables. In each step, the variable that gives the largest decrease in the value of the information criterion specified in the CRITER= option (AIC or SBC) is added. The process stops when the next candidate to be added does not reduce the value of the information criterion by more than the amount specified in the LSTOP= option in the MODEL statement.

Backward elimination starts from a larger subset of variables. In each step, one variable is dropped based on the information criterion chosen.

Variable Selection Using Penalized Likelihood

Variable selection in the linear regression context can be achieved by adding some form of penalty on the regression coefficients. One particular such form is $L_{1}$ norm penalty, which leads to LASSO:

$\min _{\beta }\left\Vert Y-X\beta \right\Vert ^{2}+\lambda \sum _{j=1}^{p}\left\vert \beta _{j}\right\vert$

This penalty method is becoming more popular in linear regression, because of the computational development in the recent years. However, how to generalize the penalty method for variable selection to the more general statistical models is not trivial. Some work has been done for the generalized linear models, in the sense that the likelihood depends on the data through a linear combination of the parameters and the data:

$l\left( \beta |x\right) =l\left( x^{T}\beta \right)$

In the more general form, the likelihood as a function of the parameters can be denoted by $l(\theta )=\sum _{i}l_{i}\left( \theta \right)$ , where $\theta$ is a vector that can include any parameters and $l(\cdot )$ is the likelihood for each observation. For example, in the Poisson model, $\theta =(\beta _0,\beta _1,\ldots ,\beta _ p)$ , and in the negative binomial model $\theta =(\beta _0,\beta _1,\ldots ,\beta _ p,\alpha )$ . The following discussion introduces the penalty method using the Poisson model as an example, but it applies similarly to the negative binomial model. The penalized likelihood function takes the form

$\begin{equation} Q\left( \beta \right) =\sum _{i}l_{i}\left( \beta \right) -n\sum _{j=1}^{p}p_{\lambda _{j}}\left( \left\vert \beta _{j}\right\vert \right) \end{equation}$

Some desired properties for the penalty functions are unbiasedness, sparsity, and continuity. Unbiasedness means that the coefficients should be unbiased for significant variables. Sparsity means that the coefficients can be exactly zero when the penalty is large enough. Continuity means that the solution of the penalized problem is continuous in the data, which means that a small perturbation of the data does not change the estimation significantly.

The $\ L_{1}$ norm penalty function used in the calculation is specified as:

$p_{\lambda }\left( \left\vert \beta \right\vert \right) =\lambda$

The main challenge for this penalized likelihood method is on the computation side. The penalty function is nondifferentiable at zero, which poses a computational problem for the optimization. To get around this nondifferentiability problem, Fan and Li (2001) suggest a local quadratic approximation for the penalty function. However, it is later found that the numerical performance is not satisfactory in a few aspects. Zou and Li (2008) proposed local linear approximation (LLA) to solve the problem numerically. The algorithm replaces the penalty function with a linear approximation around a fixed point $\beta ^{(0)}$ :

$p_{\lambda }\left( \left\vert \beta _{j}\right\vert \right) \approx p_{\lambda }\left( \left\vert \beta _{j}^{\left( 0\right) }\right\vert \right) +p_{\lambda }^{\prime }\left( \left\vert \beta _{j}^{\left( 0\right) }\right\vert \right) \left( \left\vert \beta _{j}\right\vert -\left\vert \beta _{j}^{\left( 0\right) }\right\vert \right)$

Then the problem can be solved iteratively. Start from $\beta ^{(0)} = \hat{\beta }_ M$ , which denotes the usual MLE estimate. For iteration ,

$\beta ^{\left( k+1\right) }=\arg \max _\beta \left\{ \sum _{i}l_{i}\left( \beta \right) -n\sum _{j=1}^{p}p_{\lambda }^{\prime }\left( \left\vert \beta _{j}^{( k) }\right\vert \right) \left\vert \beta _{j}\right\vert \right\}$

The algorithm stops when $\| \beta ^{(k+1)}-\beta ^{(k)}\|$ is small. To save computing time, you can also choose a maximum number of iterations. This number can be specified by the LLASTEPS= option.

The objective function is nondifferentiable. The optimization problem can be solved using an optimization methods with contraints, by a variable transformation

$\begin{equation} \beta _ j =\beta _ j^+ -\beta _ j^-, \beta _ j^+ \ge 0 , \beta _ j^-\ge 0 \end{equation}$

For each fixed tuning parameter $\lambda$ , you can solve the preceding optimization problem to obtain an estimate for $\beta$ . Due to the property of the norm penalty, some of the coefficients in $\beta$ can be exactly zero. The remaining question is to choose the best tuning parameter $\lambda$ . You can use either of the approaches described in the following subsections.

The GCV Approach

In this approach, the generalized cross-validation criteria (GCV) is computed for each value of $\lambda$ on a predetermined grid $\{ \lambda _1,\ldots ,\lambda _ L\}$ ; the value of $\lambda$ that achieves the minimum of the GCV is the optimal tuning parameter. The maximum value $\lambda _ L$ can be determined by lemma 1 in Park and Hastie (2007) as follows. Suppose $\beta _0$ is free of penalty in the objective function. Let $\hat{\beta }_0$ be the MLE of $\beta _0$ by forcing the rest of the parameters to be zero. Then the maximum value of $\lambda$ is

$\displaystyle \lambda _ L$	$\displaystyle = \arg \max _\lambda \left\{ \max _\lambda : \left\|\frac{\partial l}{\partial \beta _ j}(\hat{\beta }_0)\right\| \le n P’_\lambda (\|\beta _ j\|) ,j=1,\ldots ,p \right\}$
$\displaystyle$	$\displaystyle = \arg \max _\lambda \left\{ \left\|\frac1n \frac{\partial l}{\partial \beta _ j}(\hat{\beta }_0)\right\| ,j=1,\ldots ,p \right\}$

You can compute the GCV by using the LASSO framework. In the last step of Newton-Raphson approximation, you have

$\frac12 \min _\beta {\Bigl \| (\nabla ^2 l(\beta ^{(k)}))^{1/2}(\beta -\beta ^{(k)})+(\nabla ^2 l(\beta ^{(k)}))^{-1/2} \nabla l(\beta ^{(k)})\Bigr \| ^2 +n\sum _{j=1}^ p p’_\lambda (|\beta _ j^{(k)}|) |\beta _ j|}$

The solution $\hat{\beta }$ satisfies

$\hat{\beta } -\beta ^{(k)} = -(\nabla ^2 l(\beta ^{(k)}) -2W^-)^{-1} \left( \nabla l(\beta ^{(k)}) - 2\mathbf{b}\right)$

where

$\displaystyle W^-$	$\displaystyle = n \text {diag}(W^-_{1},\ldots , W^-_{p} )$
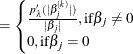$\displaystyle W^{-}_ j$	$\displaystyle = \begin{cases} \frac{p_\lambda (\|\beta _ j^{(k)}\|)}{\|\beta _ j\|}, \text {if} \beta _ j \ne 0\\ 0, \text {if} \beta _ j = 0 \end{cases}$
$\displaystyle \mathbf{b}$	$\displaystyle = n \text {diag}(p’_\lambda (\|\beta _1^{(k)}\|)\text {sgn}(\beta _1),\ldots ,p’_\lambda (\|\beta _ p^{(k)}\|)\text {sgn}(\beta _ p))$

Note that the intercept term has no penalty on its absolute value, and therefore the $W^{-}_ j$ term that corresponds to the intercept is 0. More generally, you can make any parameter (such as the $\alpha$ in the negative binomial model) in the likelihood function free of penalty, and you treat them the same as the intercept.

The effective number of parameters is

$\displaystyle e(\lambda )$	$\displaystyle = \text {tr} \left\{ \left(\nabla ^2 l(\beta ^{(k)})\right)^{1/2}\Bigl (\nabla ^2 l(\beta ^{(k)}) -2W^-\Bigr )^{-1} \left(\nabla ^2 l(\beta ^{(k)})\right)^{1/2} \right\}$
$\displaystyle$	$\displaystyle = \text {tr} \left\{ \Bigl (\nabla ^2 l(\beta ^{(k)}) -2 W^- \Bigr )^{-1} \nabla ^2 l(\beta ^{(k)}) \right\}$

and the generalized cross-validation error is

$\text {GCV}(\lambda )= \frac{l(\hat{\beta })}{n[1-e(\lambda )/n]^2}$

The GCV1 Approach

Another form of GCV uses the number of nonzero coefficients as the degrees-of-freedom:

$\displaystyle e_1 (\lambda )$	$\displaystyle = \sum _{j=0}^ p \mathbf{1}_{[\beta _ j \ne 0]}$
$\displaystyle \text {GCV}_1(\lambda )$	$\displaystyle = \frac{l(\hat{\beta })}{n[1-e_1(\lambda )/n]^2}$

The standard errors follow the sandwich formula

$\displaystyle \text {cov}(\hat{\beta })$	$\displaystyle = \left\{ \nabla ^2 l(\beta ^{(k)}) -2W^-\right\} ^{-1} \widehat{\text {cov}}\left( \nabla l(\beta ^{(k)}) - 2\mathbf{b}\right) \left\{ \nabla ^2 l(\beta ^{(k)}) -2W^-\right\} ^{-1}$
$\displaystyle$	$\displaystyle =\left\{ \nabla ^2 l(\beta ^{(k)}) -2W^-\right\} ^{-1} \widehat{\text {cov}}\left( \nabla l(\beta ^{(k)}) \right) \left\{ \nabla ^2 l(\beta ^{(k)}) -2W^-\right\} ^{-1}$

It is common practice to report only the standard errors of the nonzero parameters.

The TCOUNTREG Procedure (Experimental)