The SIMILARITY Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 AccumulationMissing Value InterpretationZero Value InterpretationTime Series TransformationTime Series DifferencingTime Series Missing Value TrimmingTime Series Descriptive StatisticsInput and Target SequencesSliding SequencesTime WarpingSequence NormalizationSequence ScalingSimilarity MeasuresUser-Defined Functions and SubroutinesOutput Data SetsOUT= Data SetOUTMEASURE= Data SetOUTPATH= Data SetOUTSEQUENCE= Data SetOUTSUM= Data Set_STATUS_ Variable ValuesPrinted OutputODS Table NamesODS Graphics
AccumulationMissing Value InterpretationZero Value InterpretationTime Series TransformationTime Series DifferencingTime Series Missing Value TrimmingTime Series Descriptive StatisticsInput and Target SequencesSliding SequencesTime WarpingSequence NormalizationSequence ScalingSimilarity MeasuresUser-Defined Functions and SubroutinesOutput Data SetsOUT= Data SetOUTMEASURE= Data SetOUTPATH= Data SetOUTSEQUENCE= Data SetOUTSUM= Data Set_STATUS_ Variable ValuesPrinted OutputODS Table NamesODS Graphics -
Examples

- References
Time Series Transformation
Transformations are useful when you want to stabilize the time series before computing the similarity measures. There are
four transformations available, for strictly positive series only. Let ![]() be the original time series, and let
be the original time series, and let ![]() be the transformed series. The transformations are defined as follows:
be the transformed series. The transformations are defined as follows:
- Log
-
is the logarithmic transformation,
![\[ w_{t} = \mr {ln}(y_{t}) \]](images/etsug_similarity0026.png)
- Logistic
-
is the logistic transformation,
![\[ w_{t} = \mr {ln}(c y_{t} / (1-c y_{t})) \]](images/etsug_similarity0027.png)
where the scaling factor
 is
is
![\[ c = (1-e^{-6}) 10 ^{- \mr {ceil}( \mr {log}_{10}({max}( y_{t}) ))} \]](images/etsug_similarity0029.png)
and
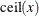 is the smallest integer greater than or equal to x.
is the smallest integer greater than or equal to x.
- Square root
-
is the square root transformation,
![\[ w_{t} = \sqrt {y_{t}} \]](images/etsug_similarity0031.png)
- Box-Cox
-
is the Box-Cox transformation,
![\[ w_{t} = \begin{cases} \frac{y_{t}^{{\lambda }} - 1}{\lambda } & {\lambda } {\ne } 0 \\ \mr {ln}( y_{t}) & {\lambda } = 0 \end{cases} \]](images/etsug_similarity0032.png)
- User-Defined
-
is the transformation computed by a user-defined subroutine that is created by using the FCMP procedure, where User-Defined is the subroutine name.
Other time series transformations can be performed prior to invoking the SIMILARITY procedure by using the SAS/ETS EXPAND procedure or the DATA step.