FIT Statement
FIT < equations > < PARMS=( parameter <values> …) > < START=( parameter values …) > < DROP=( parameter …) > < INITIAL=( variable
<= parameter | constant > …) > < / options > ;
The FIT statement estimates model parameters by fitting the model equations to input data and optionally selects the equations to be fit. If the list of equations is omitted, all model equations that contain parameters are fitted.
The following options can be used in the FIT statement.
- DROP= ( parameters …)
-
specifies that the named parameters not be estimated. All the parameters in the equations fit are estimated except those listed in the DROP= option. The dropped parameters retain their previous values and are not changed by the estimation.
- INITIAL= ( variable = < parameter | constant > …)
-
associates a variable with an initial value as a parameter or a constant. This option applies only to ordinary differential equations. See the section Ordinary Differential Equations for more information.
- PARMS= ( parameters [values] …)
-
selects a subset of the parameters for estimation. When the PARMS= option is used, only the named parameters are estimated. Any parameters not specified in the PARMS= list retain their previous values and are not changed by the estimation.
In PROC MODEL, you have several options to specify starting values for the parameters to be estimated. When more than one option is specified, the options are implemented in the following order of precedence (from highest to lowest): the START= option, the PARMS statement initialization value, the ESTDATA= option, and the PARMSDATA= option. If no options are specified for the starting value, the default value of 0.0001 is used.
- PRL= WALD | LR | BOTH
-
requests confidence intervals on estimated parameters. By default, the PRL option produces 95% likelihood ratio confidence limits. The coverage of the confidence interval is controlled by the ALPHA= option in the FIT statement.
- START= ( parameter values …)
-
supplies starting values for the parameter estimates. In PROC MODEL, you have several options to specify starting values for the parameters to be estimated. When more than one option is specified, the options are implemented in the following order of precedence (from highest to lowest): the START= option, the PARMS statement initialization value, the ESTDATA= option, and the PARMSDATA= option. If no options are specified for the starting value, the default value of 0.0001 is used. If the START= option specifies more than one starting value for one or more parameters, a grid search is performed over all combinations of the values, and the best combination is used to start the iterations. For more information, see the STARTITER= option.
Options to Control the Estimation Method Used
- ADJSMMV
-
specifies adding the variance adjustment from simulating the moments to the variance-covariance matrix of the parameter estimators. By default, no adjustment is made.
- COVBEST=GLS | CROSS | FDA
-
specifies the variance-covariance estimator used for FIML. COVBEST=GLS selects the generalized least squares estimator. COVBEST=CROSS selects the crossproducts estimator. COVBEST=FDA selects the inverse of the finite difference approximation to the Hessian. The default is COVBEST=CROSS.
- DYNAMIC
-
specifies dynamic estimation of ordinary differential equations. See the section Ordinary Differential Equations for more details.
- FIML
- GINV=G2 | G4
-
specifies the type of generalized inverse to be used when computing the covariance matrix. G4 selects the Moore-Penrose generalized inverse. The default is GINV=G2.
Rather than deleting linearly related rows and columns of the covariance matrix, the Moore-Penrose generalized inverse averages the variance effects between collinear rows. When the option GINV=G4 is used, the Moore-Penrose generalized inverse is used to calculate standard errors and the covariance matrix of the parameters as well as the change vector for the optimization problem. For singular systems, a normal G2 inverse is used to determine the singular rows so that the parameters can be marked in the parameter estimates table. A G2 inverse is calculated by satisfying the first two properties of the Moore-Penrose generalized inverse; that is,
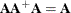 and
and 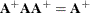 . Whether or not you use a G4 inverse, if the covariance matrix is singular, the parameter estimates are not unique. Refer
to Noble and Daniel (1977, pp. 337–340) for more details about generalized inverses.
. Whether or not you use a G4 inverse, if the covariance matrix is singular, the parameter estimates are not unique. Refer
to Noble and Daniel (1977, pp. 337–340) for more details about generalized inverses.
- GENGMMV
-
specify GMM variance under arbitrary weighting matrix. See the section Estimation Methods for more details.
This is the default method for GMM estimation.
- GMM
- HCCME= 0 | 1 | 2 | 3 | NO
-
specifies the type of heteroscedasticity-consistent covariance matrix estimator to use for OLS, 2SLS, 3SLS, SUR, and the iterated versions of these estimation methods. The number corresponds to the type of covariance matrix estimator to use as
![\[ \begin{array}{cl} HC_0: & \hat{\epsilon }^2_ t \\ HC_1: & \frac{ n}{n-df}\hat{\epsilon }^2_ t \\ HC_2: & \hat{\epsilon }^2_ t/ (1-\hat{h}_ t) \\ HC_3: & \hat{\epsilon }^2_ t/ (1-\hat{h}_ t)^2 \end{array} \]](images/etsug_model0086.png)
The default is NO.
- ITGMM
-
specifies iterated generalized method of moments estimation.
- ITOLS
-
specifies iterated ordinary least squares estimation. This is the same as OLS unless there are cross-equation parameter restrictions.
- ITSUR
-
specifies iterated seemingly unrelated regression estimation
- IT2SLS
-
specifies iterated two-stage least squares estimation. This is the same as 2SLS unless there are cross-equation parameter restrictions.
- IT3SLS
-
KERNEL=(PARZEN | BART | QS, <c> , <e> )
KERNEL=PARZEN | BART | QS -
specifies the kernel to be used for GMM and ITGMM. PARZEN selects the Parzen kernel, BART selects the Bartlett kernel, and QS selects the quadratic spectral kernel.
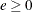 and
and 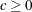 are used to compute the bandwidth parameter. The default is KERNEL=(PARZEN, 1, 0.2). See the section Estimation Methods for more details.
are used to compute the bandwidth parameter. The default is KERNEL=(PARZEN, 1, 0.2). See the section Estimation Methods for more details.
- N2SLS | 2SLS
-
specifies nonlinear two-stage least squares estimation. This is the default when an INSTRUMENTS statement is used.
- N3SLS | 3SLS
- NDRAW <=number of draws>
-
requests the simulation method for parameter estimation where the contribution of each observation to the estimation is approximated by using number of draws evaluations of the model program. If number of draws is not specified, the default value of 10 is used.
-
NOOLS
NO2SLS -
specifies bypassing OLS or 2SLS to get initial parameter estimates for GMM, ITGMM, or FIML. This is important for certain models that are poorly defined in OLS or 2SLS, or if good initial parameter values are already provided. Note that for GMM, the V matrix is created by using the initial values specified and this might not be consistently estimated.
- NO3SLS
-
specifies not to use 3SLS automatically for FIML initial parameter starting values.
- NOGENGMMV
-
specifies not to use GMM variance under arbitrary weighting matrix. Use GMM variance under optimal weighting matrix instead. See the section Estimation Methods for more details.
- NPREOBS =number of obs to initialize
-
specifies the initial number of observations to run the simulation before the simulated values are compared to observed variables. This option is most useful in cases where the program statements involve lag operations. Use this option to avoid the effect of the starting point on the simulation.
- NVDRAW =number of draws for V matrix
-
specifies
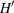 , the number of draws for V matrix. If this option is not specified, the default
, the number of draws for V matrix. If this option is not specified, the default 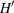 is set to 20.
is set to 20.
- OLS
-
specifies ordinary least squares estimation. This is the default.
- SUR
- VARDEF=N | WGT | DF | WDF
-
specifies the denominator to be used in computing variances and covariances, MSE, root MSE measures, and so on. VARDEF=N specifies that the number of nonmissing observations be used. VARDEF=WGT specifies that the sum of the weights be used. VARDEF=DF specifies that the number of nonmissing observations minus the model degrees of freedom (number of parameters) be used. VARDEF=WDF specifies that the sum of the weights minus the model degrees of freedom be used. The default is VARDEF=DF. For FIML estimation the VARDEF= option does not affect the calculation of the parameter covariance matrix, which is determined by the COVBEST= option.
Data Set Options
- DATA=SAS-data-set
-
specifies the input data set. Values for the variables in the program are read from this data set. If the DATA= option is not specified on the FIT statement, the data set specified by the DATA= option on the PROC MODEL statement is used.
- ESTDATA=SAS-data-set
-
specifies a data set whose first observation provides initial values for some or all of the parameters.
- MISSING=PAIRWISE | DELETE
-
specifies how missing values are handled. MISSING=PAIRWISE specifies that missing values are tracked on an equation-by-equation basis. MISSING=DELETE specifies that the entire observation is omitted from the analysis when any equation has a missing predicted or actual value for the equation. The default is MISSING=DELETE.
- OUT=SAS-data-set
-
names the SAS data set to contain the residuals, predicted values, or actual values from each estimation. The residual values written to the OUT= data set are defined as the
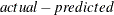 , which is the negative of RESID.variable as defined in the section Equation Translations. Only the residuals are output by default.
, which is the negative of RESID.variable as defined in the section Equation Translations. Only the residuals are output by default.
- OUTACTUAL
-
writes the actual values of the endogenous variables of the estimation to the OUT= data set. This option is applicable only if the OUT= option is specified.
- OUTALL
-
selects the OUTACTUAL, OUTERRORS, OUTLAGS, OUTPREDICT, and OUTRESID options.
-
OUTCOV
COVOUT -
writes the covariance matrix of the estimates to the OUTEST= data set in addition to the parameter estimates. The OUTCOV option is applicable only if the OUTEST= option is also specified.
- OUTEST=SAS-data-set
-
names the SAS data set to contain the parameter estimates and optionally the covariance of the estimates.
- OUTLAGS
-
writes the observations used to start the lags to the OUT= data set. This option is applicable only if the OUT= option is specified.
- OUTPREDICT
-
writes the predicted values to the OUT= data set. This option is applicable only if OUT= is specified.
- OUTRESID
-
writes the residual values computed from the parameter estimates to the OUT= data set. The OUTRESID option is the default if neither OUTPREDICT nor OUTACTUAL is specified. This option is applicable only if the OUT= option is specified. If the h.var equation is specified, the residual values written to the OUT= data set are the normalized residuals, defined as
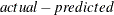 , divided by the square root of the h.var value. If the WEIGHT statement is used, the residual values are calculated as
, divided by the square root of the h.var value. If the WEIGHT statement is used, the residual values are calculated as 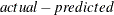 multiplied by the square root of the WEIGHT variable.
multiplied by the square root of the WEIGHT variable.
- OUTS=SAS-data-set
-
names the SAS data set to contain the estimated covariance matrix of the equation errors. This is the covariance of the residuals computed from the parameter estimates.
- OUTSN=SAS-data-set
-
names the SAS data set to contain the estimated normalized covariance matrix of the equation errors. This is valid for multivariate t distribution estimation.
- OUTSUSED=SAS-data-set
-
names the SAS data set to contain the S matrix used in the objective function definition. The OUTSUSED= data set is the same as the OUTS= data set for the methods that iterate the S matrix.
- OUTUNWGTRESID
-
writes the unweighted residual values computed from the parameter estimates to the OUT= data set. These are residuals computed as
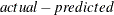 with no accounting for the WEIGHT statement, the _WEIGHT_ variable, or any variance expressions. This option is applicable
only if the OUT= option is specified.
with no accounting for the WEIGHT statement, the _WEIGHT_ variable, or any variance expressions. This option is applicable
only if the OUT= option is specified.
- OUTV=SAS-data-set
-
names the SAS data set to contain the estimate of the variance matrix for GMM and ITGMM.
- SDATA=SAS-data-set
-
specifies a data set that provides the covariance matrix of the equation errors. The matrix read from the SDATA= data set is used for the equation covariance matrix (S matrix) in the estimation. (The SDATA= S matrix is used to provide only the initial estimate of S for the methods that iterate the S matrix.)
- TIME=name
-
specifies the name of the time variable. This variable must be in the data set.
- TYPE=name
-
specifies the estimation type to read from the SDATA= and ESTDATA= data sets. The name specified in the TYPE= option is compared to the _TYPE_ variable in the ESTDATA= and SDATA= data sets to select observations to use in constructing the covariance matrices. When the TYPE= option is omitted, the last estimation type in the data set is used. Valid values are the estimation methods used in PROC MODEL.
- VDATA=SAS-data-set
-
specifies a data set that contains a variance matrix for GMM and ITGMM estimation. See the section Output Data Sets for details.
Printing Options for FIT Tasks
- BREUSCH=( variable-list )
-
specifies the modified Breusch-Pagan test, where variable-list is a list of variables used to model the error variance.
-
CHOW=obs
CHOW=(obs1 obs2 …obsn) -
prints the Chow test for break points or structural changes in a model. The argument is the number of observations in the first sample or a parenthesized list of first sample sizes. If the size of the one of the two groups in which the sample is partitioned is less than the number of parameters, then a predictive Chow test is automatically used. See the section Chow Tests for details.
- COLLIN
-
prints collinearity diagnostics for the Jacobian crossproducts matrix (XPX) after the parameters have converged. Collinearity diagnostics are also automatically printed if the estimation fails to converge.
- CORR
-
prints the correlation matrices of the residuals and parameters. Using CORR is the same as using both CORRB and CORRS.
- CORRB
- CORRS
- COV
-
prints the covariance matrices of the residuals and parameters. Specifying COV is the same as specifying both COVB and COVS.
- COVB
- COVS
- DW <=>
-
prints Durbin-Watson
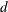 statistics, which measure autocorrelation of the residuals. When the residual series is interrupted by missing observations,
the Durbin-Watson statistic calculated is
statistics, which measure autocorrelation of the residuals. When the residual series is interrupted by missing observations,
the Durbin-Watson statistic calculated is 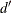 as suggested by Savin and White (1978). This is the usual Durbin-Watson computed by ignoring the gaps. Savin and White show
that it has the same null distribution as the DW with no gaps in the series and can be used to test for autocorrelation using
the standard tables. The Durbin-Watson statistic is not valid for models that contain lagged endogenous variables.
as suggested by Savin and White (1978). This is the usual Durbin-Watson computed by ignoring the gaps. Savin and White show
that it has the same null distribution as the DW with no gaps in the series and can be used to test for autocorrelation using
the standard tables. The Durbin-Watson statistic is not valid for models that contain lagged endogenous variables.
You can use the DW= option to request higher-order Durbin-Watson statistics. Since the ordinary Durbin-Watson statistic tests only for first-order autocorrelation, the Durbin-Watson statistics for higher-order autocorrelation are called generalized Durbin-Watson statistics.
- DWPROB
-
prints the significance level (p-values) for the Durbin-Watson tests. Since the Durbin-Watson p-values are computationally expensive, they are not reported by default. In the Durbin-Watson test, the null hypothesis is that there is autocorrelation at a specific lag.
See the section “Generalized Durbin-Watson Tests” for limitations of the statistic in the Chapter 8: The AUTOREG Procedure.
- FSRSQ
-
prints the first-stage R
 statistics for instrumental estimation methods. These R
statistics for instrumental estimation methods. These R statistics measure the proportion of the variance retained when the Jacobian columns associated with the parameters are projected
through the instruments space.
statistics measure the proportion of the variance retained when the Jacobian columns associated with the parameters are projected
through the instruments space.
- GODFREY
- GODFREY=n
-
performs Godfrey’s tests for autocorrelated residuals for each equation, where n is the maximum autoregressive order, and specifies that Godfrey’s tests be computed for lags 1 through n. The default number of lags is one.
- HAUSMAN
- NORMAL
-
PCHOW=obs
PCHOW=(obs1 obs2 …obsn) -
prints the predictive Chow test for break points or structural changes in a model. The argument is the number of observations in the first sample or a parenthesized list of first sample sizes. See the section Chow Tests for details.
- PRINTALL
-
specifies the printing options COLLIN, CORRB, CORRS, COVB, COVS, DETAILS, DW, and FSRSQ.
- WHITE
Options to Control Iteration Output
Details of the output produced are discussed in the section Iteration History.
- I
-
prints the inverse of the crossproducts Jacobian matrix at each iteration.
- ITALL
-
specifies all iteration printing-control options (I, ITDETAILS, ITPRINT, and XPX). ITALL also prints the crossproducts matrix (labeled CROSS), the parameter change vector, and the estimate of the cross-equation covariance of residuals matrix at each iteration.
- ITDETAILS
-
prints a detailed iteration listing. This includes the ITPRINT information and additional statistics.
- ITPRINT
-
prints the parameter estimates, objective function value, and convergence criteria at each iteration.
- XPX
Options to Control the Minimization Process
The following options can be helpful when you experience a convergence problem:
-
CONVERGE=value1
CONVERGE=(value1, value2) -
specifies the convergence criteria. The convergence measure must be less than value1 before convergence is assumed. value2 is the convergence criterion for the S and V matrices for S and V iterated methods. value2 defaults to value1. See the section Convergence Criteria for details. The default value is CONVERGE=0.001.
- HESSIAN=CROSS | GLS | FDA
-
specifies the Hessian approximation used for FIML. HESSIAN=CROSS selects the crossproducts approximation to the Hessian, HESSIAN=GLS selects the generalized least squares approximation to the Hessian, and HESSIAN=FDA selects the finite difference approximation to the Hessian. HESSIAN=GLS is the default.
- LTEBOUND=n
-
specifies the local truncation error bound for the integration. This option is ignored if no ordinary differential equations (ODEs) are specified.
- EPSILON =value
-
specifies the tolerance value used to transform strict inequalities into inequalities when restrictions on parameters are imposed. By default, EPSILON=1E–8. See the section Restrictions and Bounds on Parameters for details.
- MAXITER=n
-
specifies the maximum number of iterations allowed. The default is MAXITER=100.
- MAXSUBITER=n
-
specifies the maximum number of subiterations allowed for an iteration. For the GAUSS method, the MAXSUBITER= option limits the number of step halvings. For the MARQUARDT method, the MAXSUBITER= option limits the number of times
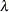 can be increased. The default is MAXSUBITER=30. See the section Minimization Methods for details.
can be increased. The default is MAXSUBITER=30. See the section Minimization Methods for details.
- METHOD=GAUSS | MARQUARDT
-
specifies the iterative minimization method to use. METHOD=GAUSS specifies the Gauss-Newton method, and METHOD=MARQUARDT specifies the Marquardt-Levenberg method. The default is METHOD=GAUSS. If the default GAUSS method fails to converge, the procedure switches to the MARQUARDT method. See the section Minimization Methods for details.
- MINTIMESTEP=n
-
specifies the smallest allowed time step to be used in the integration. This option is ignored if no ODEs are specified.
- NESTIT
-
changes the way the iterations are performed for estimation methods that iterate the estimate of the equation covariance (S matrix). The NESTIT option is relevant only for the methods that iterate the estimate of the covariance matrix (ITGMM, ITOLS, ITSUR, IT2SLS, and IT3SLS). See the section Details on the Covariance of Equation Errors for an explanation of NESTIT.
- SINGULAR=value
-
specifies the smallest pivot value allowed. The default 1.0E–12.
- STARTITER=n
-
specifies the number of minimization iterations to perform at each grid point. The default is STARTITER=0, which implies that no minimization is performed at the grid points. See the section Using the STARTITER Option for more details.
Other Options
Other options that can be used on the FIT statement include the following that list and analyze the model: BLOCK, GRAPH, LIST, LISTCODE, LISTDEP, LISTDER, and XREF. The following printing control options are also available: DETAILS, FLOW, INTGPRINT, MAXERRORS=, NOPRINT, PRINTALL, and TRACE. For complete descriptions of these options, see the discussion of the PROC MODEL statement options earlier in this chapter.