Chow Tests
The Chow test is used to test for break points or structural changes in a model. The problem is posed as a partitioning of
the data into two parts of size ![]() and
and ![]() . The null hypothesis to be tested is
. The null hypothesis to be tested is
|
|
where ![]() is estimated by using the first part of the data and
is estimated by using the first part of the data and ![]() is estimated by using the second part.
is estimated by using the second part.
The test is performed as follows (see Davidson and MacKinnon 1993, p. 380).
-
The
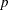 parameters of the model are estimated.
parameters of the model are estimated.
-
A second linear regression is performed on the residuals,
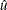 , from the nonlinear estimation in step one.
, from the nonlinear estimation in step one.
![\[ \hat{u} = \hat{\mi {\bX } }b + \mr {residuals} \]](images/etsug_model0638.png)
where
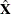 is Jacobian columns that are evaluated at the parameter estimates. If the estimation is an instrumental variables estimation
with matrix of instruments
is Jacobian columns that are evaluated at the parameter estimates. If the estimation is an instrumental variables estimation
with matrix of instruments 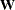 , then the following regression is performed:
, then the following regression is performed:
![\[ \hat{u} = \mi {\bP }_{{W}^{{\ast }}}\hat{\mi {\bX } } b + \mr {residuals} \]](images/etsug_model0641.png)
where
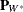 is the projection matrix.
is the projection matrix.
-
The restricted SSE (RSSE) from this regression is obtained. An SSE for each subsample is then obtained by using the same linear regression.
-
The F statistic is then
![\[ f = \frac{(\mi {RSSE} -\mi {SSE}_{1} - \mi {SSE}_{2})/p}{(\mi {SSE} _{1}+\mi {SSE}_{2})/(n-2p)} \]](images/etsug_model0643.png)
This test has
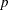 and
and 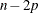 degrees of freedom.
degrees of freedom.
Chow’s test is not applicable if ![]() , since one of the two subsamples does not contain enough data to estimate
, since one of the two subsamples does not contain enough data to estimate ![]() . In this instance, the predictive Chow test can be used. The predictive Chow test is defined as
. In this instance, the predictive Chow test can be used. The predictive Chow test is defined as
|
|
where ![]() . This test can be derived from the Chow test by noting that the
. This test can be derived from the Chow test by noting that the ![]() when
when ![]() and by adjusting the degrees of freedom appropriately.
and by adjusting the degrees of freedom appropriately.
You can select the Chow test and the predictive Chow test by specifying the CHOW=arg and the PCHOW=arg options in the FIT statement, where arg is either the number of observations in the first sample or a parenthesized list of first sample sizes. If the size of the one of the two groups in which the sample is partitioned is less than the number of parameters, then a predictive Chow test is automatically used. These tests statistics are not produced for GMM and FIML estimations.
The following is an example of the use of the Chow test.
data exp;
x=0;
do time=1 to 100;
if time=50 then x=1;
y = 35 * exp( 0.01 * time ) + rannor( 123 ) + x * 5;
output;
end;
run;
proc model data=exp;
parm zo 35 b;
dert.z = b * z;
y=z;
fit y init=(z=zo) / chow =(40 50 60) pchow=90;
run;
The data set introduces an artificial structural change into the model (the structural change effects the intercept parameter). The output from the requested Chow tests are shown in Figure 19.57.
Figure 19.57: Chow’s Test Results
| Structural Change Test | |||||
|---|---|---|---|---|---|
| Test | Break Point | Num DF | Den DF | F Value | Pr > F |
| Chow | 40 | 2 | 96 | 12.95 | <.0001 |
| Chow | 50 | 2 | 96 | 101.37 | <.0001 |
| Chow | 60 | 2 | 96 | 26.43 | <.0001 |
| Predictive Chow | 90 | 11 | 87 | 1.86 | 0.0566 |