The ENTROPY Procedure (Experimental)

Pure Inverse Problems

First-Order Markov Process Estimation

A special case of systems of equations estimation is the pure inverse problem. A pure problem is one that contains an exact relationship between the dependent variable and the independent variables and does not have an error component. A pure inverse problem can be written as

$\mb {y} = X \beta$

where $\mb {y}$ is a -dimensional vector of observations, $\mb {X}$ is a $n \times k$ matrix of regressors, and $\beta$ is a -dimensional vector of unknowns. Notice that there is no error term.

A classic example is a dice problem (Jaynes, 1963). Given a six-sided die that can take on the values and the average outcome of the die , compute the probabilities $\beta = (p_1, p_2, \cdots , p_6)’$ of rolling each number. This infers six values from two pieces of information. The data points are the expected value of y, and the sum of the probabilities is one. Given , this problem is solved by using the following SAS code:

data one;
   array x[6] ( 1 2 3 4 5 6 );
   y=4.0;
run;

proc entropy data=one pure;
   priors x1 0 1 x2 0 1 x3 0 1 x4 0 1 x5 0 1 x6 0 1;
   model y = x1-x6/ noint;
   restrict x1 + x2 +x3 +x4 + x5 + x6 =1;
run;

The probabilities are given in Figure 13.16.

Figure 13.16: Jaynes’ Dice Pure Inverse Problem

Prior Distribution of Parameter T

The ENTROPY Procedure

GME Variable Estimates
Variable	Estimate	Information Index	Label
x1	0.101763	0.5254
x2	0.122658	0.4630
x3	0.147141	0.3974
x4	0.175533	0.3298
x5	0.208066	0.2622
x6	0.244839	0.1970
Restrict0	2.388082	.	x1 + x2 + x3 + x4 + x5 + x6 = 1

Note how the probabilities are skewed to the higher values because of the high average roll provided in the input data.

First-Order Markov Process Estimation

A more useful inverse problem is the first-order markov process. Companies have a share of the marketplace where they do business. Generally, customers for a specific market space can move from company to company. The movement of customers can be visualized graphically as a flow diagram, as in Figure 13.17. The arrows represent movements of customers from one company to another.

Figure 13.17: Markov Transition Diagram

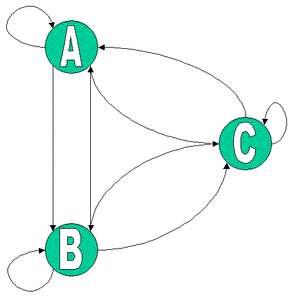
You can model the probability that a customer moves from one company to another using a first-order Markov model. Mathematically the model is:

$y_ t = P y_{t-1}$

where is a vector of market shares at time and is a $k\times k$ matrix of unknown transition probabilities. The value $p_{ij}$ represents the probability that a customer who is currently using company at time moves to company at time . The diagonal elements then represent the probability that a customer stays with the current company. The columns in sum to one.

Given market share information over time, you can estimate the transition probabilities . In order to estimate using traditional methods, you need at least observations. If you have fewer than transitions, you can use the ENTROPY procedure to estimate the probabilities.

Suppose you are studying the market share for four companies. If you want to estimate the transition probabilities for these four companies, you need a time series with four observations of the shares. Assume the current transition probability matrix is as follows:

$\left[ \begin{array}{cccc} 0.7 & 0.4 & 0.0 & 0.1 \\ 0.1 & 0.5 & 0.4 & 0.0 \\ 0.0 & 0.1 & 0.6 & 0.0 \\ 0.2 & 0.0 & 0.0 & 0.9 \end{array} \right]$

The following SAS DATA step statements generate a series of market shares from this probability matrix. A transition is represented as the current period shares, y, and the previous period shares, x.

data m;
            /* Known Transition matrix */
   array p[4,4] (0.7 .4 .0 .1
                 0.1 .5 .4 .0
                 0.0 .1 .6 .0
                 0.2 .0 .0 .9 ) ;
            /* Initial Market shares */
   array y[4] y1-y4 ( .4 .3 .2 .1 );
   array x[4] x1-x4;
   drop p1-p16 i;
   do i = 1 to 3;
       x[1] = y[1]; x[2] = y[2];
       x[3] = y[3]; x[4] = y[4];
       y[1] = p[1,1] * x1 + p[1,2] * x2 + p[1,3] * x3 + p[1,4] * x4;
       y[2] = p[2,1] * x1 + p[2,2] * x2 + p[2,3] * x3 + p[2,4] * x4;
       y[3] = p[3,1] * x1 + p[3,2] * x2 + p[3,3] * x3 + p[3,4] * x4;
       y[4] = p[4,1] * x1 + p[4,2] * x2 + p[4,3] * x3 + p[4,4] * x4;
       output;
   end;
run;

The following SAS statements estimate the transition matrix by using only the first transition.

proc entropy markov pure data=m(obs=1);
   model y1-y4 = x1-x4;
run;

The MARKOV option implies NOINT for each model, that the sum of the parameters in each column is one, and chooses support points of and . This model can be expressed equivalently as

proc entropy pure data=m(obs=1) ;
   priors y1.x1 0 1 y1.x2 0 1 y1.x3 0 1 y1.x4 0 1;
   priors y2.x1 0 1 y2.x2 0 1 y2.x3 0 1 y2.x4 0 1;
   priors y3.x1 0 1 y3.x2 0 1 y3.x3 0 1 y3.x4 0 1;
   priors y4.x1 0 1 y4.x2 0 1 y4.x3 0 1 y4.x4 0 1;

   model y1 = x1-x4 / noint;
   model y2 = x1-x4 / noint;
   model y3 = x1-x4 / noint;
   model y4 = x1-x4 / noint;

   restrict y1.x1 + y2.x1 + y3.x1 + y4.x1 = 1;
   restrict y1.x2 + y2.x2 + y3.x2 + y4.x2 = 1;
   restrict y1.x3 + y2.x3 + y3.x3 + y4.x3 = 1;
   restrict y1.x4 + y2.x4 + y3.x4 + y4.x4 = 1;
run;

The transition matrix is given in Figure 13.18.

Figure 13.18: Estimate of by Using One Transition

Prior Distribution of Parameter T

The ENTROPY Procedure

GME Variable Estimates
Variable	Estimate	Information Index
y1.x1	0.463407	0.0039
y1.x2	0.41055	0.0232
y1.x3	0.356272	0.0605
y1.x4	0.302163	0.1161
y2.x1	0.272755	0.1546
y2.x2	0.271459	0.1564
y2.x3	0.267252	0.1625
y2.x4	0.260084	0.1731
y3.x1	0.119926	0.4709
y3.x2	0.148481	0.3940
y3.x3	0.180224	0.3194
y3.x4	0.214394	0.2502
y4.x1	0.143903	0.4056
y4.x2	0.169504	0.3434
y4.x3	0.196252	0.2856
y4.x4	0.223364	0.2337

Note that varies greatly from the true solution.

If two transitions are used instead (OBS=2), the resulting transition matrix is shown in Figure 13.19.

proc entropy markov pure data=m(obs=2);
   model y1-y4 = x1-x4;
run;

Figure 13.19: Estimate of by Using Two Transitions

Prior Distribution of Parameter T

The ENTROPY Procedure

GME Variable Estimates
Variable	Estimate	Information Index
y1.x1	0.721012	0.1459
y1.x2	0.355703	0.0609
y1.x3	0.026095	0.8256
y1.x4	0.096654	0.5417
y2.x1	0.083987	0.5839
y2.x2	0.53886	0.0044
y2.x3	0.373668	0.0466
y2.x4	0.000133	0.9981
y3.x1	0.000062	0.9990
y3.x2	0.099848	0.5315
y3.x3	0.600104	0.0291
y3.x4	7.871E-8	1.0000
y4.x1	0.194938	0.2883
y4.x2	0.00559	0.9501
y4.x3	0.000133	0.9981
y4.x4	0.903214	0.5413

This transition matrix is much closer to the actual transition matrix.

If, in addition to the transitions, you had other information about the transition matrix, such as your own company’s transition values, that information can be added as restrictions to the parameter estimates. For noisy data, the PURE option should be dropped. Note that this example has six zero probabilities in the transition matrix; the accurate estimation of transition matrices with fewer zero probabilities generally requires more transition observations.