The X11 Procedure

Motivation

The seasonal component of this time series, 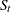, is defined as the intrayear variation that is repeated constantly (stable) or in an evolving fashion from year to year (moving seasonality). If the increase in the seasonal factors from year to year is too large, then the seasonal factors will introduce distortion into the model. It is important to determine if seasonality is identifiable without distorting the series.

To determine if stable seasonality is present in a series, PROC X11 computes a one-way analysis of variance by using the seasons (months or quarters) as the factor on the Final Unmodified SI Ratios (Table D8). This is the appropriate table to use because the removal of the trend cycle is equivalent to detrending. PROC X11 prints this test, labeled "Stable Seasonality Test," immediately after the Table D8.

The X11 seasonal adjustment method tests for moving seasonality. Moving seasonality can be a source of distortion when seasonal factors are used in the model. PROC X11 computes and prints a test for moving seasonality. The test is a two-way analysis of variance that uses months (or quarters) and years. As in the "Stable Seasonality Test," this analysis of variance is performed on the Final Unmodified SI Ratios (Table D8). PROC X11 prints this test, labeled "Moving Seasonality Test," after the "Stable Seasonality Test."

PROC X11 next computes a nonparametric Kruskal-Wallis chi-squared test for stable seasonality, "Nonparametric Test for the Presence of Seasonality Assuming Stability." The Kruskal-Wallis test is performed on the ranks of the Final Unmodified SI Ratios (Table D8). For further details about the Kruskal-Wallis test, see Lehmann (1998, pp. 204–210).

The results of the preceding three tests are combined into a joint test to measure identifiable seasonality, "Summary of Results and Combined Test for the Presence of Identifiable Seasonality." This test combines the two F tests previously described, along with the Kruskal-Wallis chi-squared test for stable seasonality, to determine "identifiable" seasonality. This test is printed after "Nonparametric Test for the Presence of Seasonality Assuming Stability."

Interpretation and Statistical Details

The "Stable Seasonality Test" is a one-way analysis of variance on the "Final Unmodified SI Ratios" with seasons (months or quarters) as the factor.

To determine whether stable seasonality is present in a series, PROC X11 computes a one-way analysis of variance by using the seasons (months or quarters) as the factor on the Final Unmodified SI Ratios (Table D8). This is the appropriate table to use because the removal of the trend cycle is similar to detrending.

A large F statistic and a small significance level are evidence that a significant amount of variation in the SI-ratios is due to months or quarters, which in turn is evidence of seasonality; the null hypothesis of no month/quarter effect is rejected.

Conversely, a small F statistic and a large significance level (close to 1.0) are evidence that variation due to month or quarter could be due to random error, and the null hypothesis of no month/quarter effect is not rejected. The interpretation and utility of seasonal adjustment are problematic under such conditions.

The F test for moving seasonality is performed by a two-way analysis of variance. The two factors are seasons (months or quarters) and years. The years effect is tested separately; the null hypothesis is no effect due to years after accounting for variation due to months or quarters. For further details about the moving seasonality test, see Lothian (1984a, 1984b, 1978) and Higginson (1975).

The significance level reported in both the moving and stable seasonality tests are only approximate. Table D8, the Final Unmodified SI Ratios, is constructed from an averaging operation that induces a correlation in the residuals from which the F test is computed. Hence the computed F statistic differs from an exact F statistic; see Cleveland and Devlin (1980) for details.

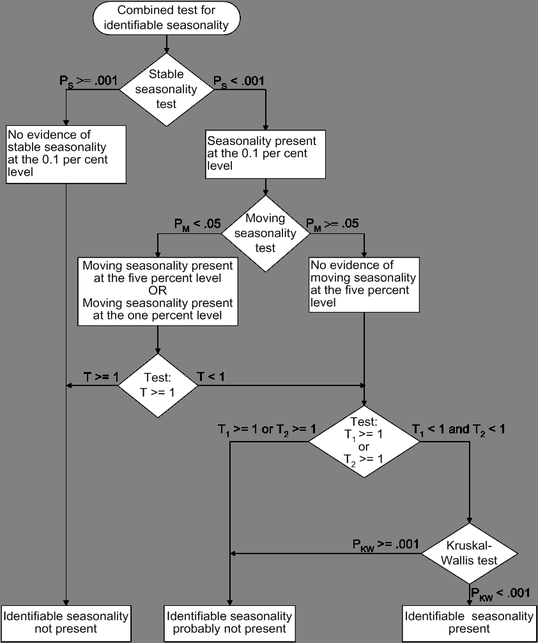
The test for identifiable seasonality is performed by combining the F tests for stable and moving seasonality, along with a Kruskal-Wallis test for stable seasonality. The following description is based on Lothian and Morry (1978b); other details can be found in Dagum (1988, 1983).

Let and 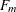denote the F value for the stable and moving seasonality tests, respectively. The combined test is performed as shown in Figure 36.5 and as follows:

1. If the null hypothesis of no stable seasonality is not rejected at the 0.10% significance level (), then the series is considered to be nonseasonal. PROC X11 returns the conclusion, "Identifiable Seasonality Not Present."

2. If the null hypothesis in step 1 is rejected, then PROC X11 computes the following quantities:

   Let denote the simple average of 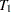and :

   If the null hypothesis of no moving seasonality is rejected at the 5.0% significance level (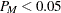) and if , the null hypothesis of identifiable seasonality not present is not rejected and PROC X11 returns the conclusion, "Identifiable Seasonality Not Present."

3. If the null hypothesis of identifiable seasonality not present has not been accepted, but , , 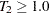or the Kruskal-Wallis chi-squared test fails to reject at the 0.10% significance level (), then PROC X11 returns the conclusion "Identifiable Seasonality Probably Not Present."

4. If the null hypotheses of no stable seasonality associated with the 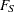and Kruskal-Wallis chi-squared tests are rejected and if none of the combined measures described in steps 2 and 3 fail, then the null hypothesis of identifiable seasonality not present is rejected and PROC X11 returns the conclusion "Identifiable Seasonality Present."

Figure 36.5 Combined Seasonality Test Flowchart

Table S 0.A

Table S 0.A gives the variable name, the length and number of spans, and the beginning and ending dates of each span.

Table S 0.B

Table S 0.B gives the summary of the two F tests performed during the standard X11 seasonal adjustments for stable and moving seasonality on Table D8, the final SI ratios. These tests are described in the section Printed Output.

Table S 1.A

Table S 1.A gives the range analysis of seasonal factors. This includes the means for each month (or quarter) within a span, the maximum percentage difference across spans for each month, and the average. The minimum and maximum within a span are also indicated.

For example, for a monthly series and an analysis with four spans, the January row would contain a column for each span, with the value representing the average seasonal factor (Table D10) over all January calendar months occurring within the span. Beside each span column is a character column with either a MIN, MAX, or blank value, indicating which calendar month had the minimum and maximum value over that span.

Denote the average over the 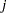th calendar month in span 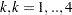, by ; then the maximum percent difference (MPD) for month 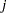is defined by

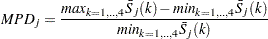The last numeric column of Table S 1.A is the average value over all spans for each calendar month, with the minimum and maximum row flagged as in the span columns.

Table S 1.B

Table S 1.B gives a summary of range measures for each span. The first column, Range Means, is calculated by computing the maximum and minimum over all months or quarters in a span, then taking the difference. The next column is the range ratio means, which is simply the ratio of the previously described maximum and minimum. The next two columns are the minimum and maximum seasonal factors over the entire span, while the range sf column is the difference of these. Finally, the last column is the ratio of the Max SF and Min SF columns.

Breakdown Tables

Table S 2.A.1 begins the breakdown analysis for the various series considered in the sliding spans analysis. The key concept here is the MPD described above in the section Table S 1.A and in the section Computational Details for Sliding Spans Analysis. For a month or quarter that appears in two or more spans, the maximum percentage difference is computed and tested against a cutoff level. If it exceeds this cutoff, it is counted as an instance of exceeding the level. It is of interest to see if such instances fall disproportionately in certain months and years. Tables S 2.A.1 through S 6.A.3 display this breakdown for all series considered.

Table S 2.A.1

Table S 2.A.1 gives the monthly (quarterly) breakdown for the seasonal factors (table D10). The first column identifies the month or quarter. The next column is the number of times the MPD for D10 exceeded 3.0%, followed by the total count. The last is the average maximum percentage difference for the corresponding month or quarter.

Table S 2.A.2

Table S 2.A.2 gives the same information as Table S 2.A.1, but on a yearly basis.

Table S 2.A.3

The description of Table S 2.A.3 requires the definition of "Sign Change" and "Turning Point."

First, some motivation. Recall that for a highly stable series, adding or deleting a small number of observations should not affect the estimation of the various components of a seasonal adjustment procedure.

Consider Table D10, the seasonal factors in a sliding spans analysis that uses four spans. For a given observation , looking across the four spans, we can easily pick out large differences if they occur. More subtle differences can occur when estimates go from above to below (or vice versa) a base level. In the case of multiplicative model, the seasonal factors have a base level of 100.0. So it is useful to enumerate those instances where both a large change occurs (an MPD value exceeding 3.0%) and a change of sign (with respect to the base) occur.

Let denote the base value (which in general depends on the component being considered and the model type, multiplicative or additive). If, for span 1, (1) is below (i.e., 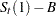is negative) and for some subsequent span 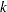, is above (i.e., 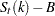is positive), then a positive "Change in Sign" has occurred at observation . Similarly, if, for span 1, (1) is above , and for some subsequent span 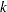, is below , then a negative "Change in Sign" has occurred. Both cases, positive or negative, constitute a "Change in Sign"; the actual direction is indicated in tables S 7.A through S 7.E, which are described below.

Another behavior of interest occurs when component estimates increase then decrease (or vice versa) across spans for a given observation. Using the preceding example, the seasonal factors at observation could first increase, then decrease across the four spans.

This behavior, combined with an MPD exceeding the level, is of interest in questions of stability.

Again, consider Table D10, the seasonal factors in a sliding spans analysis that uses four spans. For a given observation (containing at least three spans), note the level of D10 for the first span. Continue across the spans until a difference of 1.0% or greater occurs (or no more spans are left), noting whether the difference is up or down. If the difference is up, continue until a difference of 1.0% or greater occurs downward (or no more spans are left). If such an up-down combination occurs, the observation is counted as an up-down turning point. A similar description occurs for a down-up turning point. Tables S 7.A through S 7.E, described below, show the occurrence of turning points, indicating whether up-down or down-up. Note that it requires at least three spans to test for a turning point. Hence Tables S 2.A.3 through S 6.A.3 show a reduced number in the "Turning Point" row for the "Total Tested" column, and in Tables S 7.A through S 7.E, the turning points symbols can occur only where three or more spans overlap.

With these descriptions of sign change and turning point, we now describe Table S 2.A.3. The first column gives the type or category, the second column gives the total number of observations falling into the category, the third column gives the total number tested, and the last column gives the percentage for the number found in the category.

The first category (row) of the table is for flagged observations—that is, those observations where the MPD exceeded the appropriate cutoff level (3.0% is default for the seasonal factors). The second category is for level changes, while the third category is for turning points. The fourth category is for flagged sign changes—that is, for those observations that are sign changes, how many are also flagged. Note the total tested column for this category equals the number found for sign change, reflecting the definition of the fourth category.

The fifth column is for flagged turning points—that is, for those observations that are turning points, how many are also flagged.

The footnote to Table S 2.A.3 gives the U.S. Census Bureau recommendation for thresholds, as described in the section Computational Details for Sliding Spans Analysis.

Table S 2.B

Table S 2.B gives the histogram of flagged for seasonal factors (Table D10) using the appropriate cutoff value (default 3.0%). This table looks at the spread of the number of times the MPD exceeded the corresponding level. The range is divided up into four intervals: 3.0%–4.0%, 4.0%–5.0%, 5.0%–6.0%, and greater than 6.0%. The first column shows the symbol used in Table S 7.A, the second column gives the range in interval notation, and the last column gives the number found in the corresponding interval. Note that the sum of the last column should agree with the "Number Found" column of the "Flagged MPD" row in Table S 2.A.3.

Table S 2.C

Table S 2.C gives selected percentiles for the MPD for the seasonal factors (Table D10).

Tables S 3.A.1 through S 3.A.3

These table relate to the trading-day factors (Table C18) and follow the same format as Tables S 2.A.1 through S 2.A.3. The only difference between these tables and Tables S 2.A.1 through S 2.A.3 is the default cutoff value of 2.0% instead of the 3.0% used for the seasonal factors.

Tables S 3.B, S 3.C

These tables, applied to the trading-day factors (Table C18), are the same format as Tables S 2.B through S 2.C. The default cutoff value is different, with corresponding differences in the intervals in S 3.B.

Tables S 4.A.1 through S 4.A.3

These tables relate to the seasonally adjusted series (Table D11) and follow the same format as Tables S 2.A.1 through S 2.A.3. The same default cutoff value of 3.0% is used.

Tables S 4.B, S 4.C

These tables, applied to the seasonally adjusted series (Table D11), are the same format as tables S 2.B through S 2.C.

Tables S 5.A.1 through S 5.A.3

These table relate to the month-to-month (or quarter-to-quarter) differences in the seasonally adjusted series, and follow the same format as Tables S 2.A.1 through S 2.A.3. The same default cutoff value of 3.0% is used.

Tables S 5.B, S 5.C

These tables, applied to the month-to-month (or quarter-to-quarter) differences in the seasonally adjusted series, are the same format as tables S 2.B through S 2.C. The same default cutoff value of 3.0% is used.

Tables S 6.A.1 through S 6.A.3

These table relate to the year-to-year differences in the seasonally adjusted series, and follow the same format as Tables S 2.A.1 through S 2.A.3. The same default cutoff value of 3.0% is used.

Tables S 6.B, S 6.C

These tables, applied to the year-to-year differences in the seasonally adjusted series, are the same format as tables S 2.B through S 2.C. The same default cutoff value of 3.0% is used.

Table S 7.A

Table S 7.A gives the entire listing of the seasonal factors (Table D10) for each span. The first column gives the date for each observation included in the spans. Note that the dates do not cover the entire original data set. Only those observations included in one or more spans are listed.

The next 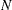columns (where 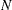is the number of spans) are the individual spans starting at the earliest span. The span columns are labeled by their beginning and ending dates.

Following the last span is the "Sign Change" column. As explained in the description of Table S 2.A.3, a sign change occurs at a given observation when the seasonal factor estimates go from above to below, or below to above, a base level. For the seasonal factors, 100.0 is the base level for the multiplicative model, 0.0 for the additive model. A blank value indicates no sign change, a "U" indicates a movement "upward" from the base level and a "D" indicates a movement "downward" from the base level.

The next column is the "Turning Point" column. As explained in the description of Table S 2.A.3, a turning point occurs when there is an upward then downward movement, or downward then upward movement, of sufficient magnitude. A blank value indicates no turning point, a "U-D" indicates a movement "upward then downward," and a "D-U" indicates a movement "downward then upward."

The next column is the maximum percentage difference (MPD). This quantity, described in the section Computational Details for Sliding Spans Analysis, is the main computation for sliding spans analysis. A measure of how extreme the MPD value is given in the last column, the "Level of Excess" column. The symbols used and their meaning are described in Table S 2.A.3. If a given observation has exceeded the cutoff, the level of excess column is blank.

Table S 7.B

Table S 7.B gives the entire listing of the trading-day factors (Table C18) for each span. The format of this table is exactly like that of Table S 7.A.

Table S 7.C

Table S 7.C gives the entire listing of the seasonally adjusted data (Table D11) for each span. The format of this table is exactly like that of Table S 7.A except for the "Sign Change" column, which is not printed. The seasonally adjusted data have the same units as the original data; there is no natural base level as in the case of a percentage. Hence the sign change is not appropriate for D11.

Table S 7.D

Table S 7.D gives the entire listing of the month-to-month (or quarter-to-quarter) changes in seasonally adjusted data for each span. The format of this table is exactly like that of Table S 7.A.

Table S 7.E

Table S 7.E gives the entire listing of the year-to-year changes in seasonally adjusted data for each span. The format of this table is exactly like that of Table S 7.A.