The QLIM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Ordinal Discrete Choice Modeling Limited Dependent Variable Models Stochastic Frontier Production and Cost Models Heteroscedasticity and Box-Cox Transformation Bivariate Limited Dependent Variable Modeling Selection Models Multivariate Limited Dependent Models Tests on Parameters Output to SAS Data Set OUTEST= Data Set Naming ODS Table Names
Ordinal Discrete Choice Modeling Limited Dependent Variable Models Stochastic Frontier Production and Cost Models Heteroscedasticity and Box-Cox Transformation Bivariate Limited Dependent Variable Modeling Selection Models Multivariate Limited Dependent Models Tests on Parameters Output to SAS Data Set OUTEST= Data Set Naming ODS Table Names -
Examples

- References
Example 22.1 Ordered Data Modeling
Cameron and Trivedi (1986) studied Australian Health Survey data. Variable definitions are given in Cameron and Trivedi (1998, p. 68).
The dependent variable, dvisits, has nine ordered values. The following SAS statements estimate the ordinal probit model:
/*-- Ordered Discrete Responses --*/
proc qlim data=docvisit;
model dvisits = sex age agesq income levyplus
freepoor freerepa illness actdays hscore
chcond1 chcond2 / discrete;
run;
The output of the QLIM procedure for ordered data modeling is shown in Output 22.1.1.
| Binary Data |
| Discrete Response Profile of dvisits | ||
|---|---|---|
| Index | Value | Total Frequency |
| 1 | 0 | 4141 |
| 2 | 1 | 782 |
| 3 | 2 | 174 |
| 4 | 3 | 30 |
| 5 | 4 | 24 |
| 6 | 5 | 9 |
| 7 | 6 | 12 |
| 8 | 7 | 12 |
| 9 | 8 | 6 |
| Model Fit Summary | |
|---|---|
| Number of Endogenous Variables | 1 |
| Endogenous Variable | dvisits |
| Number of Observations | 5190 |
| Log Likelihood | -3138 |
| Maximum Absolute Gradient | 0.0003675 |
| Number of Iterations | 82 |
| Optimization Method | Quasi-Newton |
| AIC | 6316 |
| Schwarz Criterion | 6447 |
| Goodness-of-Fit Measures | ||
|---|---|---|
| Measure | Value | Formula |
| Likelihood Ratio (R) | 789.73 | 2 * (LogL - LogL0) |
| Upper Bound of R (U) | 7065.9 | - 2 * LogL0 |
| Aldrich-Nelson | 0.1321 | R / (R+N) |
| Cragg-Uhler 1 | 0.1412 | 1 - exp(-R/N) |
| Cragg-Uhler 2 | 0.1898 | (1-exp(-R/N)) / (1-exp(-U/N)) |
| Estrella | 0.149 | 1 - (1-R/U)^(U/N) |
| Adjusted Estrella | 0.1416 | 1 - ((LogL-K)/LogL0)^(-2/N*LogL0) |
| McFadden's LRI | 0.1118 | R / U |
| Veall-Zimmermann | 0.2291 | (R * (U+N)) / (U * (R+N)) |
| McKelvey-Zavoina | 0.2036 | |
| N = # of observations, K = # of regressors | ||
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | -1.378705 | 0.147413 | -9.35 | <.0001 |
| sex | 1 | 0.131885 | 0.043785 | 3.01 | 0.0026 |
| age | 1 | -0.534190 | 0.815907 | -0.65 | 0.5126 |
| agesq | 1 | 0.857308 | 0.898364 | 0.95 | 0.3399 |
| income | 1 | -0.062211 | 0.068017 | -0.91 | 0.3604 |
| levyplus | 1 | 0.137030 | 0.053262 | 2.57 | 0.0101 |
| freepoor | 1 | -0.346045 | 0.129638 | -2.67 | 0.0076 |
| freerepa | 1 | 0.178382 | 0.074348 | 2.40 | 0.0164 |
| illness | 1 | 0.150485 | 0.015747 | 9.56 | <.0001 |
| actdays | 1 | 0.100575 | 0.005850 | 17.19 | <.0001 |
| hscore | 1 | 0.031862 | 0.009201 | 3.46 | 0.0005 |
| chcond1 | 1 | 0.061601 | 0.049024 | 1.26 | 0.2089 |
| chcond2 | 1 | 0.135321 | 0.067711 | 2.00 | 0.0457 |
| _Limit2 | 1 | 0.938884 | 0.031219 | 30.07 | <.0001 |
| _Limit3 | 1 | 1.514288 | 0.049329 | 30.70 | <.0001 |
| _Limit4 | 1 | 1.711660 | 0.058151 | 29.43 | <.0001 |
| _Limit5 | 1 | 1.952860 | 0.072014 | 27.12 | <.0001 |
| _Limit6 | 1 | 2.087422 | 0.081655 | 25.56 | <.0001 |
| _Limit7 | 1 | 2.333786 | 0.101760 | 22.93 | <.0001 |
| _Limit8 | 1 | 2.789796 | 0.156189 | 17.86 | <.0001 |
By default, ordinal probit/logit models are estimated assuming that the first threshold or limit parameter (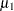 ) is 0. However, this parameter can also be estimated when the LIMIT1=VARYING option is specified. The probability that
) is 0. However, this parameter can also be estimated when the LIMIT1=VARYING option is specified. The probability that 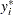 belongs to the
belongs to the 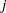 th category is defined as
th category is defined as
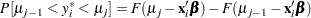 |
where 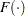 is the logistic or standard normal CDF,
is the logistic or standard normal CDF, 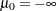 and
and  . Output 22.1.2 lists ordinal probit estimates computed in the following program. Note that the intercept term is suppressed for model identification when
. Output 22.1.2 lists ordinal probit estimates computed in the following program. Note that the intercept term is suppressed for model identification when 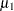 is estimated.
is estimated.
/*-- Ordered Probit --*/
proc qlim data=docvisit;
model dvisits = sex age agesq income levyplus
freepoor freerepa illness actdays hscore
chcond1 chcond2 / discrete(d=normal) limit1=varying;
run;
| Binary Data |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| sex | 1 | 0.131885 | 0.043785 | 3.01 | 0.0026 |
| age | 1 | -0.534181 | 0.815915 | -0.65 | 0.5127 |
| agesq | 1 | 0.857298 | 0.898371 | 0.95 | 0.3399 |
| income | 1 | -0.062211 | 0.068017 | -0.91 | 0.3604 |
| levyplus | 1 | 0.137031 | 0.053262 | 2.57 | 0.0101 |
| freepoor | 1 | -0.346045 | 0.129638 | -2.67 | 0.0076 |
| freerepa | 1 | 0.178382 | 0.074348 | 2.40 | 0.0164 |
| illness | 1 | 0.150485 | 0.015747 | 9.56 | <.0001 |
| actdays | 1 | 0.100575 | 0.005850 | 17.19 | <.0001 |
| hscore | 1 | 0.031862 | 0.009201 | 3.46 | 0.0005 |
| chcond1 | 1 | 0.061602 | 0.049024 | 1.26 | 0.2089 |
| chcond2 | 1 | 0.135322 | 0.067711 | 2.00 | 0.0457 |
| _Limit1 | 1 | 1.378706 | 0.147415 | 9.35 | <.0001 |
| _Limit2 | 1 | 2.317590 | 0.150206 | 15.43 | <.0001 |
| _Limit3 | 1 | 2.892994 | 0.155198 | 18.64 | <.0001 |
| _Limit4 | 1 | 3.090367 | 0.158263 | 19.53 | <.0001 |
| _Limit5 | 1 | 3.331566 | 0.164065 | 20.31 | <.0001 |
| _Limit6 | 1 | 3.466128 | 0.168799 | 20.53 | <.0001 |
| _Limit7 | 1 | 3.712493 | 0.179756 | 20.65 | <.0001 |
| _Limit8 | 1 | 4.168502 | 0.215738 | 19.32 | <.0001 |