Example 19.16 Simulated Method of Moments—AR(1) Process
This example illustrates how to use SMM to estimate an AR(1) regression model for the following process:
In the following SAS statements, 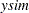 is simulated by using this model, and the endogenous variable
is simulated by using this model, and the endogenous variable 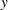 is set to be equal to
is set to be equal to 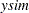 . The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before
. The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before 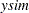 is compared to the first observation of
is compared to the first observation of 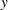 . Because the initial
. Because the initial  is zero, the first
is zero, the first 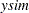 is
is 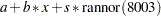 . Without the NPREOBS option, this
. Without the NPREOBS option, this 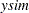 is matched with the first observation of
is matched with the first observation of 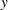 . With NPREOBS, this
. With NPREOBS, this 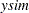 and the next nine
and the next nine 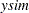 are thrown away, and the moment match starts with the eleventh
are thrown away, and the moment match starts with the eleventh 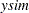 with the first observation of
with the first observation of 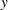 . This way, the initial values do not exert a large influence on the simulated endogenous variables.
. This way, the initial values do not exert a large influence on the simulated endogenous variables.
%let nobs=500;
data ardata;
lu =0;
do i=-10 to &nobs;
x = rannor( 1011 );
e = rannor( 1011 );
u = .6 * lu + 1.5 * e;
Y = 2 + 1.5 * x + u;
lu = u;
if i > 0 then output;
end;
run;
title1 'Simulated Method of Moments for AR(1) Process';
proc model data=ardata ;
parms a b s 1 alpha .5;
instrument x;
u = alpha * zlag(u) + s * rannor( 8003 );
ysim = a + b * x + u;
y = ysim;
moment y = (2) lag1(1);
fit y / gmm npreobs=10 ndraw=10;
bound s > 0, 1 > alpha > 0;
run;
The output of the MODEL procedure is shown in Output 19.16.1:
Output 19.16.1
PROC MODEL Output
| Y |
| a b s(1) alpha(0.5) |
| _moment_2 _moment_1 Y |
| F(a, b, s, alpha) |
| F(a, b, s, alpha) |
| F(a(1), b(x), s, alpha) |
| 1 x |
| 1.632798 |
0.1038 |
15.73 |
<.0001 |
| 1.513197 |
0.0698 |
21.67 |
<.0001 |
| 1.427888 |
0.0984 |
14.52 |
<.0001 |
| 0.543985 |
0.0809 |
6.72 |
<.0001 |
Copyright © SAS Institute Inc. All rights reserved.

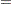
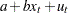
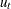
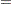
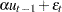

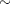
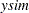 is simulated by using this model, and the endogenous variable
is simulated by using this model, and the endogenous variable 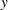 is set to be equal to
is set to be equal to 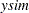 . The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before
. The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before 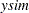 is compared to the first observation of
is compared to the first observation of 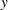 . Because the initial
. Because the initial  is zero, the first
is zero, the first 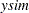 is
is 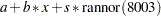 . Without the NPREOBS option, this
. Without the NPREOBS option, this 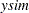 is matched with the first observation of
is matched with the first observation of 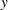 . With NPREOBS, this
. With NPREOBS, this 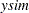 and the next nine
and the next nine 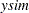 are thrown away, and the moment match starts with the eleventh
are thrown away, and the moment match starts with the eleventh 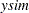 with the first observation of
with the first observation of 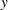 . This way, the initial values do not exert a large influence on the simulated endogenous variables.
. This way, the initial values do not exert a large influence on the simulated endogenous variables.