Example 19.15 Simulated Method of Moments—Simple Linear Regression
This example illustrates how to use SMM to estimate a simple linear regression model for the following process:
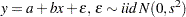 |
In the following SAS statements,  is simulated, and the first moment and the second moment of
is simulated, and the first moment and the second moment of  are compared with those of the observed endogenous variable
are compared with those of the observed endogenous variable 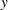 .
.
title "Simple regression model";
data regdata;
do i=1 to 500;
x = rannor( 1013 );
Y = 2 + 1.5 * x + 1.5 * rannor( 1013 );
output;
end;
run;
proc model data=regdata;
parms a b s;
instrument x;
ysim = (a+b*x) + s * rannor( 8003 );
y = ysim;
eq.ysq = y*y - ysim*ysim;
fit y ysq / gmm ndraw;
bound s > 0;
run;
Alternatively, the MOMENT statement can be used to specify the moments using the following syntax:
proc model data=regdata; parms a b s; instrument x; ysim = (a+b*x) + s * rannor( 8003 ); y = ysim; moment y = (2); fit y / gmm ndraw; bound s > 0; run;
The output of the MODEL procedure is shown in Output 19.15.1:
Output 19.15.1
PROC MODEL Output
| Simple regression model |
The MODEL Procedure
| Model Summary | |
|---|---|
| Model Variables | 1 |
| Parameters | 3 |
| Equations | 2 |
| Number of Statements | 4 |
| Model Variables | Y |
|---|---|
| Parameters | a b s |
| Equations | ysq Y |
| The 2 Equations to Estimate | |
|---|---|
| Y = | F(a(1), b(x), s) |
| ysq = | F(a, b, s) |
| Instruments | 1 x |
| Nonlinear GMM Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Approx Std Err | t Value | Approx Pr > |t| |
| a | 2.065983 | 0.0657 | 31.45 | <.0001 |
| b | 1.511075 | 0.0565 | 26.73 | <.0001 |
| s | 1.483358 | 0.0498 | 29.78 | <.0001 |