Example 19.2 A Consumer Demand Model
This example shows the estimation of a system of nonlinear consumer demand equations based on the translog functional form by using seemingly unrelated regression (SUR). Expenditure shares and corresponding normalized prices are given for three goods.
Since the shares add up to one, the system is singular; therefore, one equation is omitted from the estimation process. The choice of which equation to omit is arbitrary. The nonlinear system is first estimated in unrestricted form by the following statements:
title1 'Consumer Demand--Translog Functional Form';
title2 'Asymmetric Model';
proc model data=tlog1;
endogenous share1 share2;
parms a1 a2 b11 b12 b13 b21 b22 b23 b31 b32 b33;
bm1 = b11 + b21 + b31;
bm2 = b12 + b22 + b32;
bm3 = b13 + b23 + b33;
lp1 = log(p1);
lp2 = log(p2);
lp3 = log(p3);
share1 = ( a1 + b11 * lp1 + b12 * lp2 + b13 * lp3 ) /
( -1 + bm1 * lp1 + bm2 * lp2 + bm3 * lp3 );
share2 = ( a2 + b21 * lp1 + b22 * lp2 + b23 * lp3 ) /
( -1 + bm1 * lp1 + bm2 * lp2 + bm3 * lp3 );
fit share1 share2
start=( a1 -.14 a2 -.45 b11 .03 b12 .47 b22 .98 b31 .20
b32 1.11 b33 .71 ) / outsused=smatrix sur;
run;
A portion of the printed output produced by this example is shown in Output 19.2.1 through Output 19.2.3.
Output 19.2.1
Translog Demand Model Summary
| share1 share2 |
| a1(-0.14) a2(-0.45) b11(0.03) b12(0.47) b13 b21 b22(0.98) b23 b31(0.2) b32(1.11) b33(0.71) |
| share1 share2 |
| F(a1, b11, b12, b13, b21, b22, b23, b31, b32, b33) |
| F(a2, b11, b12, b13, b21, b22, b23, b31, b32, b33) |
Output 19.2.2
Estimation Summary for the Unrestricted Model
| NOTE: At SUR Iteration 2 CONVERGE=0.001 Criteria Met. |
The MODEL Procedure
SUR Estimation Summary
| 0.00016 |
| 0.00116 |
| 0.012106 |
| 2.921E-6 |
| 0.000078 |
| 1.749312 |
Output 19.2.3
Estimation Results for the Unrestricted Model
The MODEL Procedure
| 5.5 |
38.5 |
0.00166 |
0.000043 |
0.00656 |
0.8067 |
0.7841 |
| 5.5 |
38.5 |
0.00135 |
0.000035 |
0.00592 |
0.9445 |
0.9380 |
| -0.14881 |
0.00225 |
-66.08 |
<.0001 |
| -0.45776 |
0.00297 |
-154.29 |
<.0001 |
| 0.048382 |
0.0498 |
0.97 |
0.3379 |
| 0.43655 |
0.0502 |
8.70 |
<.0001 |
| 0.248588 |
0.0516 |
4.82 |
<.0001 |
| 0.586326 |
0.2089 |
2.81 |
0.0079 |
| 0.759776 |
0.2565 |
2.96 |
0.0052 |
| 1.303821 |
0.2328 |
5.60 |
<.0001 |
| 0.297808 |
0.1504 |
1.98 |
0.0550 |
| 0.961551 |
0.1633 |
5.89 |
<.0001 |
| 0.8291 |
0.1556 |
5.33 |
<.0001 |
The model is then estimated under the restriction of symmetry (b = b
= b ), as shown in the following statements:
), as shown in the following statements:
title2 'Symmetric Model';
proc model data=tlog1;
var share1 share2 p1 p2 p3;
parms a1 a2 b11 b12 b22 b31 b32 b33;
bm1 = b11 + b12 + b31;
bm2 = b12 + b22 + b32;
bm3 = b31 + b32 + b33;
lp1 = log(p1);
lp2 = log(p2);
lp3 = log(p3);
share1 = ( a1 + b11 * lp1 + b12 * lp2 + b31 * lp3 ) /
( -1 + bm1 * lp1 + bm2 * lp2 + bm3 * lp3 );
share2 = ( a2 + b12 * lp1 + b22 * lp2 + b32 * lp3 ) /
( -1 + bm1 * lp1 + bm2 * lp2 + bm3 * lp3 );
fit share1 share2
start=( a1 -.14 a2 -.45 b11 .03 b12 .47 b22 .98 b31 .20
b32 1.11 b33 .71 ) / sdata=smatrix sur;
run;
A portion of the printed output produced for the symmetry restricted model is shown in Output 19.2.4 and Output 19.2.5.
Output 19.2.4
Model Summary from the Restricted Model
The MODEL Procedure
| F(a1, b11, b12, b22, b31, b32, b33) |
| F(a2, b11, b12, b22, b31, b32, b33) |
Output 19.2.5
Estimation Results for the Restricted Model
The MODEL Procedure
| 4 |
40 |
0.00166 |
0.000041 |
0.00644 |
0.8066 |
0.7920 |
| 4 |
40 |
0.00139 |
0.000035 |
0.00590 |
0.9428 |
0.9385 |
| -0.14684 |
0.00135 |
-108.99 |
<.0001 |
| -0.4597 |
0.00167 |
-275.34 |
<.0001 |
| 0.02886 |
0.00741 |
3.89 |
0.0004 |
| 0.467827 |
0.0115 |
40.57 |
<.0001 |
| 0.970079 |
0.0177 |
54.87 |
<.0001 |
| 0.208143 |
0.00614 |
33.88 |
<.0001 |
| 1.102415 |
0.0127 |
86.51 |
<.0001 |
| 0.694245 |
0.0168 |
41.38 |
<.0001 |
Hypothesis testing requires that the S matrix from the unrestricted model be imposed on the restricted model, as explained in the section Tests on Parameters. The S matrix saved in the data set SMATRIX is requested by the SDATA= option.
A chi-square test is used to see if the hypothesis of symmetry is accepted or rejected. (Oc–Ou ) has a chi-square distribution asymptotically, where Oc is the constrained OBJECTIVE*N and Ou is the unconstrained OBJECTIVE*N. The degrees of freedom is equal to the difference in the number of free parameters in the two models.
In this example, Ou is 76.9697 and Oc is 78.4097, resulting in a difference of 1.44 with 3 degrees of freedom. You can obtain the probability value by using the following statements:
data _null_;
/* probchi( reduced-full, n-restrictions )*/
p = 1-probchi( 1.44, 3 );
put p=;
run;
The output from this DATA step run is  . With this
. With this 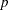 -value you cannot reject the hypothesis of symmetry. This test is asymptotically valid.
-value you cannot reject the hypothesis of symmetry. This test is asymptotically valid.
 = b
= b ), as shown in the following statements:
), as shown in the following statements:  . With this
. With this 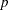 -value you cannot reject the hypothesis of symmetry. This test is asymptotically valid.
-value you cannot reject the hypothesis of symmetry. This test is asymptotically valid.