Example 8.5 Money Demand Model
This example estimates the log-log money demand equation by using the maximum likelihood method. The money demand model contains four explanatory variables. The lagged nominal money stock M1 is divided by the current price level GDF to calculate a new variable M1CP since the money stock is assumed to follow the partial adjustment process. The variable M1CP is then used to estimate the coefficient of adjustment. All variables are transformed using the natural logarithm with a DATA step. Refer to Balke and Gordon (1986) for a data description.
The first eight observations are printed using the PRINT procedure and are shown in Output 8.5.1. Note that the first observation of the variables M1CP and INFR are missing. Therefore, the money demand equation is estimated for the period 1968:2 to 1983:4 since PROC AUTOREG ignores the first missing observation. The DATA step that follows generates the transformed variables.
data money;
date = intnx( 'qtr', '01jan1968'd, _n_-1 );
format date yyqc6.;
input m1 gnp gdf ycb @@;
m = log( 100 * m1 / gdf );
m1cp = log( 100 * lag(m1) / gdf );
y = log( gnp );
intr = log( ycb );
infr = 100 * log( gdf / lag(gdf) );
label m = 'Real Money Stock (M1)'
m1cp = 'Lagged M1/Current GDF'
y = 'Real GNP'
intr = 'Yield on Corporate Bonds'
infr = 'Rate of Prices Changes';
datalines;
... more lines ...
Output 8.5.1
Money Demand Data Series – First 8 Observations
| 1968:1 |
187.15 |
1036.22 |
81.18 |
6.84 |
5.44041 |
. |
6.94333 |
1.92279 |
. |
| 1968:2 |
190.63 |
1056.02 |
82.12 |
6.97 |
5.44732 |
5.42890 |
6.96226 |
1.94162 |
1.15127 |
| 1968:3 |
194.30 |
1068.72 |
82.80 |
6.98 |
5.45815 |
5.43908 |
6.97422 |
1.94305 |
0.82465 |
| 1968:4 |
198.55 |
1071.28 |
84.04 |
6.84 |
5.46492 |
5.44328 |
6.97661 |
1.92279 |
1.48648 |
| 1969:1 |
201.73 |
1084.15 |
84.97 |
7.32 |
5.46980 |
5.45391 |
6.98855 |
1.99061 |
1.10054 |
| 1969:2 |
203.18 |
1088.73 |
86.10 |
7.54 |
5.46375 |
5.45659 |
6.99277 |
2.02022 |
1.32112 |
| 1969:3 |
204.18 |
1091.90 |
87.49 |
7.70 |
5.45265 |
5.44774 |
6.99567 |
2.04122 |
1.60151 |
| 1969:4 |
206.10 |
1085.53 |
88.62 |
8.22 |
5.44917 |
5.43981 |
6.98982 |
2.10657 |
1.28331 |
The money demand equation is first estimated using OLS. The DW=4 option produces generalized Durbin-Watson statistics up to the fourth order. Their exact marginal probabilities (p-values) are also calculated with the DWPROB option. The Durbin-Watson test indicates positive first-order autocorrelation at, say, the 10% confidence level. You can use the Durbin-Watson table, which is available only for 1% and 5% significance points. The relevant upper (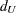 ) and lower (
) and lower (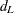 ) bounds are
) bounds are 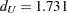 and
and 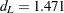 , respectively, at 5% significance level. However, the bounds test is inconvenient, since sometimes you may get the statistic in the inconclusive region while the interval between the upper and lower bounds becomes smaller with the increasing sample size. The PROC step follows:
, respectively, at 5% significance level. However, the bounds test is inconvenient, since sometimes you may get the statistic in the inconclusive region while the interval between the upper and lower bounds becomes smaller with the increasing sample size. The PROC step follows:
title 'Partial Adjustment Money Demand Equation';
title2 'Quarterly Data - 1968:2 to 1983:4';
proc autoreg data=money outest=est covout;
model m = m1cp y intr infr / dw=4 dwprob;
run;
Output 8.5.2
OLS Estimation of the Partial Adjustment Money Demand Equation
| 0.00271902 |
58 |
| 0.0000469 |
0.00685 |
| -433.68709 |
-444.40276 |
| 0.00483389 |
-443.35013 |
| 0.08888324 |
-440.18824 |
| |
0.9546 |
| |
0.9546 |
| 1.7355 |
0.0607 |
0.9393 |
| 2.1058 |
0.5519 |
0.4481 |
| 2.0286 |
0.5002 |
0.4998 |
| 2.2835 |
0.8880 |
0.1120 |
|
Note: |
Pr<DW is the p-value for testing positive autocorrelation, and Pr>DW is the p-value for testing negative autocorrelation. |
| 1 |
0.3084 |
0.2359 |
1.31 |
0.1963 |
|
| 1 |
0.8952 |
0.0439 |
20.38 |
<.0001 |
Lagged M1/Current GDF |
| 1 |
0.0476 |
0.0122 |
3.89 |
0.0003 |
Real GNP |
| 1 |
-0.0238 |
0.007933 |
-3.00 |
0.0040 |
Yield on Corporate Bonds |
| 1 |
-0.005646 |
0.001584 |
-3.56 |
0.0007 |
Rate of Prices Changes |
The autoregressive model is estimated using the maximum likelihood method. Though the Durbin-Watson test statistic is calculated after correcting the autocorrelation, it should be used with care since the test based on this statistic is not justified theoretically. The PROC step follows:
proc autoreg data=money;
model m = m1cp y intr infr / nlag=1 method=ml maxit=50;
output out=a p=p pm=pm r=r rm=rm ucl=ucl lcl=lcl
uclm=uclm lclm=lclm;
run;
proc print data=a(obs=8);
var p pm r rm ucl lcl uclm lclm;
run;
A difference is shown between the OLS estimates in Output 8.5.2 and the AR(1)-ML estimates in Output 8.5.3. The estimated autocorrelation coefficient is significantly negative 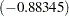 . Note that the negative coefficient of AR(1) should be interpreted as a positive autocorrelation.
. Note that the negative coefficient of AR(1) should be interpreted as a positive autocorrelation.
Two predicted values are produced: predicted values computed for the structural model and predicted values computed for the full model. The full model includes both the structural and error-process parts. The predicted values and residuals are stored in the output data set A, as are the upper and lower 95% confidence limits for the predicted values. Part of the data set A is shown in Output 8.5.4. The first observation is missing since the explanatory variables, M1CP and INFR, are missing for the corresponding observation.
Output 8.5.3
Estimated Partial Adjustment Money Demand Equation
| 0.00226719 |
57 |
| 0.0000398 |
0.00631 |
| -439.47665 |
-452.33545 |
| 0.00506044 |
-450.83545 |
| 0.09302277 |
-447.27802 |
| 232.167727 |
0.6954 |
| 2.1778 |
0.9621 |
| |
63 |
| 1 |
2.4121 |
0.4880 |
4.94 |
<.0001 |
|
| 1 |
0.4086 |
0.0908 |
4.50 |
<.0001 |
Lagged M1/Current GDF |
| 1 |
0.1509 |
0.0411 |
3.67 |
0.0005 |
Real GNP |
| 1 |
-0.1101 |
0.0159 |
-6.92 |
<.0001 |
Yield on Corporate Bonds |
| 1 |
-0.006348 |
0.001834 |
-3.46 |
0.0010 |
Rate of Prices Changes |
| 1 |
-0.8835 |
0.0686 |
-12.89 |
<.0001 |
|
| 1 |
2.4121 |
0.4685 |
5.15 |
<.0001 |
|
| 1 |
0.4086 |
0.0840 |
4.87 |
<.0001 |
Lagged M1/Current GDF |
| 1 |
0.1509 |
0.0402 |
3.75 |
0.0004 |
Real GNP |
| 1 |
-0.1101 |
0.0155 |
-7.08 |
<.0001 |
Yield on Corporate Bonds |
| 1 |
-0.006348 |
0.001828 |
-3.47 |
0.0010 |
Rate of Prices Changes |
Output 8.5.4
Partial List of the Predicted Values
| . |
. |
. |
. |
. |
. |
. |
. |
| 5.45962 |
5.45962 |
-.005763043 |
-0.012301 |
5.49319 |
5.42606 |
5.47962 |
5.43962 |
| 5.45663 |
5.46750 |
0.001511258 |
-0.009356 |
5.46954 |
5.44373 |
5.48700 |
5.44800 |
| 5.45934 |
5.46761 |
0.005574104 |
-0.002691 |
5.47243 |
5.44626 |
5.48723 |
5.44799 |
| 5.46636 |
5.46874 |
0.003442075 |
0.001064 |
5.47944 |
5.45328 |
5.48757 |
5.44991 |
| 5.46675 |
5.46581 |
-.002994443 |
-0.002054 |
5.47959 |
5.45390 |
5.48444 |
5.44718 |
| 5.45672 |
5.45854 |
-.004074196 |
-0.005889 |
5.46956 |
5.44388 |
5.47667 |
5.44040 |
| 5.44404 |
5.44924 |
0.005136019 |
-0.000066 |
5.45704 |
5.43103 |
5.46726 |
5.43122 |


 Missing Values Autoregressive Error Model Alternative Autocorrelation Correction Methods GARCH Models Heteroscedasticity Consistent Covariance Matrix Estimator Goodness-of-Fit Measures and Information Criteria Testing Predicted Values OUT= Data Set OUTEST= Data Set Printed Output ODS Table Names ODS Graphics
Missing Values Autoregressive Error Model Alternative Autocorrelation Correction Methods GARCH Models Heteroscedasticity Consistent Covariance Matrix Estimator Goodness-of-Fit Measures and Information Criteria Testing Predicted Values OUT= Data Set OUTEST= Data Set Printed Output ODS Table Names ODS Graphics
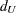 ) and lower (
) and lower (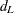 ) bounds are
) bounds are 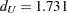 and
and 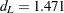 , respectively, at 5% significance level. However, the bounds test is inconvenient, since sometimes you may get the statistic in the inconclusive region while the interval between the upper and lower bounds becomes smaller with the increasing sample size. The PROC step follows:
, respectively, at 5% significance level. However, the bounds test is inconvenient, since sometimes you may get the statistic in the inconclusive region while the interval between the upper and lower bounds becomes smaller with the increasing sample size. The PROC step follows: 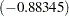 . Note that the negative coefficient of AR(1) should be interpreted as a positive autocorrelation.
. Note that the negative coefficient of AR(1) should be interpreted as a positive autocorrelation.