| The SEVERITY Procedure |
| An Example with Left-Truncation and Right-Censoring |
PROC SEVERITY enables you to specify that the response variable values are left-truncated or right-censored. The following DATA step expands the data set of the previous example to simulate a scenario that is typically encountered by an automobile insurance company. The values of the variable Y represent the loss values on claims that are reported to an auto insurance company. The variable THRESHOLD records the deductible on the insurance policy. If the actual value of Y is less than or equal to the deductible, then it is unobservable and does not get recorded. In other words, THRESHOLD specifies the left-truncation of Y. The ISCENS variable indicates whether the loss exceeds the policy limit. ISCENS=1 means that the actual value of Y is greater than the recorded value; that is, Y is right-censored. If ISCENS has any other value, then the recorded value of Y is the actual value of the loss.
/*----- Lognormal Model with left-truncation and censoring -----*/
data test_sev2(keep=y iscens threshold
label='A Lognormal Sample With Censoring and Truncation');
set test_sev1;
label y='Censored & Truncated Response';
if _n_ = 1 then call streaminit(45679);
/* make about 20% of the observations left-truncated */
if (rand('UNIFORM') < 0.2) then
threshold = y * (1 - rand('UNIFORM'));
else
threshold = .;
/* make about 15% of the observations right-censored */
iscens = (rand('UNIFORM') < 0.15);
run;
The following statements use the AICC criterion to analyze which of the four predefined distributions (lognormal, Burr, gamma, and Weibull) has the best fit for the data:
proc severity data=test_sev2
print=all plots(markcensored marktruncated)=pp;
model y(lt=threshold rc=iscens(1)) / crit=aicc;
dist logn;
dist burr;
dist gamma;
dist weibull;
run;
The MODEL statement specifies the left-truncation and right-censoring indicator variables. You need to specify that the value of 1 for the ISCENS variable indicates right-censoring, because the default indicator value is 0. Each candidate distribution needs to be specified by using a separate DIST statement. The PRINT= option in the PROC SEVERITY statement requests that all the displayed output be prepared. The PLOTS= option in the PROC SEVERITY statement requests that the P-P plots for each candidate distribution be prepared in addition to the default plots. It also instructs the procedure to mark the left-truncated and right-censored observations in the CDF plot.
Some of the key results prepared by PROC SEVERITY are shown in Figure 22.6 through Figure 22.11. The descriptive statistics of Y are shown in the second table of Figure 22.6. In addition to the estimates of the range, mean, and standard deviation of Y, the table also indicates the number of observations that are right-censored, left-truncated, and both right-censored and left-truncated. The "Model Selection Table" in Figure 22.6 shows that models with all the candidate distributions have converged and that the Logn (lognormal) model has the best fit for the data according to the AICC criterion.
| Input Data Set | |
|---|---|
| Name | WORK.TEST_SEV2 |
| Label | A Lognormal Sample With Censoring and Truncation |
| Descriptive Statistics for Variable y | |
|---|---|
| Number of Observations | 100 |
| Number of Observations Used for Estimation | 100 |
| Minimum | 2.30264 |
| Maximum | 8.34116 |
| Mean | 4.62007 |
| Standard Deviation | 1.23627 |
| Number of Left Truncated Observations | 23 |
| Number of Right Censored Observations | 14 |
| Number of Left Truncated and Right Censored Observations | 3 |
PROC SEVERITY also prepares a table that shows all the fit statistics for all the candidate models. It is useful to see which model would be the best fit according to each of the criteria. The table prepared for this example is shown in Figure 22.7. It indicates that the lognormal model is chosen by all the criteria.
| All Fit Statistics Table | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | -2 Log Likelihood |
AIC | AICC | BIC | KS | AD | CvM | |||||||
| Logn | 294.80301 | * | 298.80301 | * | 298.92672 | * | 304.01335 | * | 0.51824 | * | 0.34736 | * | 0.05159 | * |
| Burr | 296.41229 | 302.41229 | 302.66229 | 310.22780 | 0.66984 | 0.36712 | 0.05726 | |||||||
| Gamma | 295.32921 | 299.32921 | 299.45293 | 304.53955 | 0.62511 | 0.42921 | 0.05526 | |||||||
| Weibull | 305.14408 | 309.14408 | 309.26779 | 314.35442 | 0.93307 | 1.40698 | 0.17465 | |||||||
The plot that compares EDF and CDF estimates is shown in Figure 22.8. When left-truncation is specified, both the EDF and CDF estimates are conditional on the response variable being greater than the smallest left-truncation threshold in the sample. Notice the markers close to the X-axis of the plot. These indicate the values of Y that are left-truncated or right-censored.
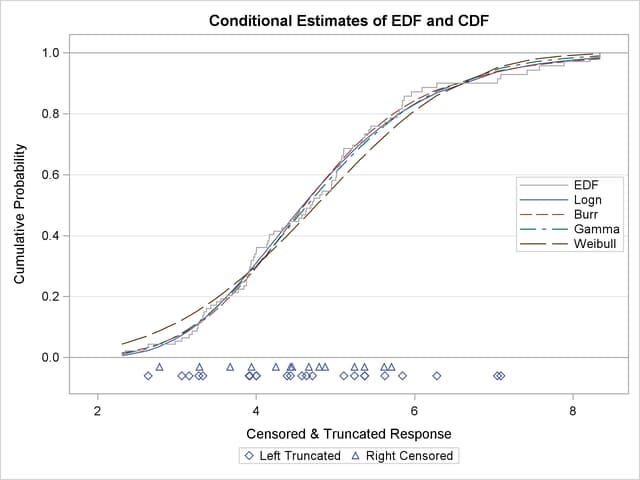
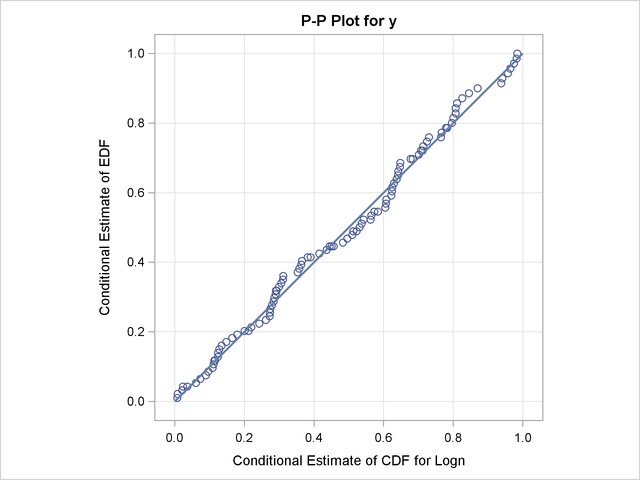
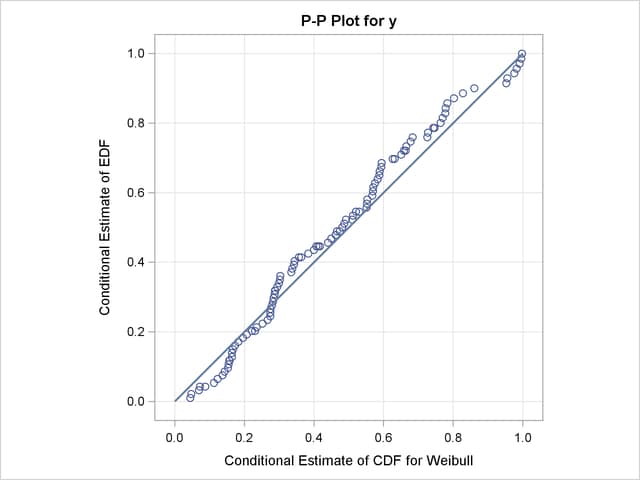
In addition to the comparative plot, PROC SEVERITY produces a P-P plot for each of the models that has not failed to converge. It is a scatter plot of the EDF and the CDF estimates. The model for which the points are scattered closer to the unit-slope reference line is a better fit. The P-P plot for the lognormal distribution is shown in Figure 22.9. It indicates that the EDF and the CDF match very closely. In contrast, the P-P plot for the Weibull distribution, also shown in Figure 22.9, indicates a poor fit.
Specifying Initial Values for Parameters
All the predefined distributions have parameter initialization functions built into them. For the current example, Figure 22.10 shows the initial values that are obtained by the predefined method for the Burr distribution. It also shows the summary of the optimization process and the final parameter estimates.
| Initial Parameter Values and Bounds for Burr Distribution |
|||
|---|---|---|---|
| Parameter | Initial Value | Lower Bound | Upper Bound |
| Theta | 4.78102 | 1.05367E-8 | Infty |
| Alpha | 2.00000 | 1.05367E-8 | Infty |
| Gamma | 2.00000 | 1.05367E-8 | Infty |
You can specify a different set of initial values if estimates are available from fitting the distribution to similar data. For this example, the parameters of the Burr distribution can be initialized with the final parameter estimates of the Burr distribution that were obtained in the first example (shown in Figure 22.5). One of the ways in which you can specify the initial values is as follows:
/*------ Specifying initial values using INIT= option -------*/
proc severity data=test_sev2 print=(all) plots=none;
model y(lt=threshold rc=iscens(1)) / crit=aicc;
dist burr init=(theta=4.62348 alpha=1.15706 gamma=6.41227);
run;
The names of the parameters specified in the INIT option must match the names used in the definition of the distribution. The results obtained with these initial values are shown in Figure 22.11. These indicate that new set of initial values causes the optimizer to reach the same solution with fewer iterations and function evaluations as compared to the default initialization.
| Optimization Summary for Burr Distribution | |
|---|---|
| Optimization Technique | Trust Region |
| Number of Iterations | 5 |
| Number of Function Evaluations | 14 |
| Log Likelihood | -148.20614 |
| Parameter Estimates for Burr Distribution | ||||
|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Theta | 4.76980 | 0.62492 | 7.63 | <.0001 |
| Alpha | 1.16363 | 0.58859 | 1.98 | 0.0509 |
| Gamma | 5.94081 | 1.05004 | 5.66 | <.0001 |
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.