| The ARIMA Procedure |
Example 7.5 Using Diagnostics to Identify ARIMA Models
Fitting ARIMA models is as much an art as it is a science. The ARIMA procedure has diagnostic options to help tentatively identify the orders of both stationary and nonstationary ARIMA processes.
Consider the Series A in Box, Jenkins, and Reinsel (1994), which consists of 197 concentration readings taken every two hours from a chemical process. Let Series A be a data set that contains these readings in a variable named X. The following SAS statements use the SCAN option of the IDENTIFY statement to generate Output 7.5.1 and Output 7.5.2. See The SCAN Method for details of the SCAN method.
/*-- Order Identification Diagnostic with SCAN Method --*/ proc arima data=SeriesA; identify var=x scan; run;
| Squared Canonical Correlation Estimates | ||||||
|---|---|---|---|---|---|---|
| Lags | MA 0 | MA 1 | MA 2 | MA 3 | MA 4 | MA 5 |
| AR 0 | 0.3263 | 0.2479 | 0.1654 | 0.1387 | 0.1183 | 0.1417 |
| AR 1 | 0.0643 | 0.0012 | 0.0028 | <.0001 | 0.0051 | 0.0002 |
| AR 2 | 0.0061 | 0.0027 | 0.0021 | 0.0011 | 0.0017 | 0.0079 |
| AR 3 | 0.0072 | <.0001 | 0.0007 | 0.0005 | 0.0019 | 0.0021 |
| AR 4 | 0.0049 | 0.0010 | 0.0014 | 0.0014 | 0.0039 | 0.0145 |
| AR 5 | 0.0202 | 0.0009 | 0.0016 | <.0001 | 0.0126 | 0.0001 |
| SCAN Chi-Square[1] Probability Values | ||||||
|---|---|---|---|---|---|---|
| Lags | MA 0 | MA 1 | MA 2 | MA 3 | MA 4 | MA 5 |
| AR 0 | <.0001 | <.0001 | <.0001 | 0.0007 | 0.0037 | 0.0024 |
| AR 1 | 0.0003 | 0.6649 | 0.5194 | 0.9235 | 0.3993 | 0.8528 |
| AR 2 | 0.2754 | 0.5106 | 0.5860 | 0.7346 | 0.6782 | 0.2766 |
| AR 3 | 0.2349 | 0.9812 | 0.7667 | 0.7861 | 0.6810 | 0.6546 |
| AR 4 | 0.3297 | 0.7154 | 0.7113 | 0.6995 | 0.5807 | 0.2205 |
| AR 5 | 0.0477 | 0.7254 | 0.6652 | 0.9576 | 0.2660 | 0.9168 |
In Output 7.5.1, there is one (maximal) rectangular region in which all the elements are insignificant with 95% confidence. This region has a vertex at (1,1). Output 7.5.2 gives recommendations based on the significance level specified by the ALPHA=siglevel option.
Another order identification diagnostic is the extended sample autocorrelation function or ESACF method. See The ESACF Method for details of the ESACF method.
The following statements generate Output 7.5.3 and Output 7.5.4:
/*-- Order Identification Diagnostic with ESACF Method --*/ proc arima data=SeriesA; identify var=x esacf; run;
| Extended Sample Autocorrelation Function | ||||||
|---|---|---|---|---|---|---|
| Lags | MA 0 | MA 1 | MA 2 | MA 3 | MA 4 | MA 5 |
| AR 0 | 0.5702 | 0.4951 | 0.3980 | 0.3557 | 0.3269 | 0.3498 |
| AR 1 | -0.3907 | 0.0425 | -0.0605 | -0.0083 | -0.0651 | -0.0127 |
| AR 2 | -0.2859 | -0.2699 | -0.0449 | 0.0089 | -0.0509 | -0.0140 |
| AR 3 | -0.5030 | -0.0106 | 0.0946 | -0.0137 | -0.0148 | -0.0302 |
| AR 4 | -0.4785 | -0.0176 | 0.0827 | -0.0244 | -0.0149 | -0.0421 |
| AR 5 | -0.3878 | -0.4101 | -0.1651 | 0.0103 | -0.1741 | -0.0231 |
| ESACF Probability Values | ||||||
|---|---|---|---|---|---|---|
| Lags | MA 0 | MA 1 | MA 2 | MA 3 | MA 4 | MA 5 |
| AR 0 | <.0001 | <.0001 | 0.0001 | 0.0014 | 0.0053 | 0.0041 |
| AR 1 | <.0001 | 0.5974 | 0.4622 | 0.9198 | 0.4292 | 0.8768 |
| AR 2 | <.0001 | 0.0002 | 0.6106 | 0.9182 | 0.5683 | 0.8592 |
| AR 3 | <.0001 | 0.9022 | 0.2400 | 0.8713 | 0.8930 | 0.7372 |
| AR 4 | <.0001 | 0.8380 | 0.3180 | 0.7737 | 0.8913 | 0.6213 |
| AR 5 | <.0001 | <.0001 | 0.0765 | 0.9142 | 0.1038 | 0.8103 |
In Output 7.5.3, there are three right-triangular regions in which all elements are insignificant at the 5% level. The triangles have vertices (1,1), (3,1), and (4,1). Since the triangle at (1,1) covers more insignificant terms, it is recommended first. Similarly, the remaining recommendations are ordered by the number of insignificant terms contained in the triangle. Output 7.5.4 gives recommendations based on the significance level specified by the ALPHA=siglevel option.
If you also specify the SCAN option in the same IDENTIFY statement, the two recommendations are printed side by side:
/*-- Combination of SCAN and ESACF Methods --*/ proc arima data=SeriesA; identify var=x scan esacf; run;
Output 7.5.5 shows the results.
| ARMA(p+d,q) Tentative Order Selection Tests |
|||
|---|---|---|---|
| SCAN | ESACF | ||
| p+d | q | p+d | q |
| 1 | 1 | 1 | 1 |
| 3 | 1 | ||
| 4 | 1 | ||
From Output 7.5.5, the autoregressive and moving-average orders are tentatively identified by both SCAN and ESACF tables to be (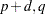 )=(1,1). Because both the SCAN and ESACF indicate a
)=(1,1). Because both the SCAN and ESACF indicate a  term of 1, a unit root test should be used to determine whether this autoregressive term is a unit root. Since a moving-average term appears to be present, a large autoregressive term is appropriate for the augmented Dickey-Fuller test for a unit root.
term of 1, a unit root test should be used to determine whether this autoregressive term is a unit root. Since a moving-average term appears to be present, a large autoregressive term is appropriate for the augmented Dickey-Fuller test for a unit root.
Submitting the following statements generates Output 7.5.6:
/*-- Augmented Dickey-Fuller Unit Root Tests --*/ proc arima data=SeriesA; identify var=x stationarity=(adf=(5,6,7,8)); run;
| Augmented Dickey-Fuller Unit Root Tests | |||||||
|---|---|---|---|---|---|---|---|
| Type | Lags | Rho | Pr < Rho | Tau | Pr < Tau | F | Pr > F |
| Zero Mean | 5 | 0.0403 | 0.6913 | 0.42 | 0.8024 | ||
| 6 | 0.0479 | 0.6931 | 0.63 | 0.8508 | |||
| 7 | 0.0376 | 0.6907 | 0.49 | 0.8200 | |||
| 8 | 0.0354 | 0.6901 | 0.48 | 0.8175 | |||
| Single Mean | 5 | -18.4550 | 0.0150 | -2.67 | 0.0821 | 3.67 | 0.1367 |
| 6 | -10.8939 | 0.1043 | -2.02 | 0.2767 | 2.27 | 0.4931 | |
| 7 | -10.9224 | 0.1035 | -1.93 | 0.3172 | 2.00 | 0.5605 | |
| 8 | -10.2992 | 0.1208 | -1.83 | 0.3650 | 1.81 | 0.6108 | |
| Trend | 5 | -18.4360 | 0.0871 | -2.66 | 0.2561 | 3.54 | 0.4703 |
| 6 | -10.8436 | 0.3710 | -2.01 | 0.5939 | 2.04 | 0.7694 | |
| 7 | -10.7427 | 0.3773 | -1.90 | 0.6519 | 1.91 | 0.7956 | |
| 8 | -10.0370 | 0.4236 | -1.79 | 0.7081 | 1.74 | 0.8293 | |
The preceding test results show that a unit root is very likely given that none of the p-values are small enough to cause you to reject the null hypothesis that the series has a unit root. Based on this test and the previous results, the series should be differenced, and an ARIMA(0,1,1) would be a good choice for a tentative model for Series A.
Using the recommendation that the series be differenced, the following statements generate Output 7.5.7:
/*-- Minimum Information Criterion --*/ proc arima data=SeriesA; identify var=x(1) minic; run;
| Minimum Information Criterion | ||||||
|---|---|---|---|---|---|---|
| Lags | MA 0 | MA 1 | MA 2 | MA 3 | MA 4 | MA 5 |
| AR 0 | -2.05761 | -2.3497 | -2.32358 | -2.31298 | -2.30967 | -2.28528 |
| AR 1 | -2.23291 | -2.32345 | -2.29665 | -2.28644 | -2.28356 | -2.26011 |
| AR 2 | -2.23947 | -2.30313 | -2.28084 | -2.26065 | -2.25685 | -2.23458 |
| AR 3 | -2.25092 | -2.28088 | -2.25567 | -2.23455 | -2.22997 | -2.20769 |
| AR 4 | -2.25934 | -2.2778 | -2.25363 | -2.22983 | -2.20312 | -2.19531 |
| AR 5 | -2.2751 | -2.26805 | -2.24249 | -2.21789 | -2.19667 | -2.17426 |
The error series is estimated by using an AR(7) model, and the minimum of this MINIC table is 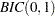 . This diagnostic confirms the previous result which indicates that an ARIMA(0,1,1) is a tentative model for Series A.
. This diagnostic confirms the previous result which indicates that an ARIMA(0,1,1) is a tentative model for Series A.
If you also specify the SCAN or MINIC option in the same IDENTIFY statement as follows, the BIC associated with the SCAN table and ESACF table recommendations is listed. Output 7.5.8 shows the results.
/*-- Combination of MINIC, SCAN, and ESACF Options --*/ proc arima data=SeriesA; identify var=x(1) minic scan esacf; run;
| ARMA(p+d,q) Tentative Order Selection Tests |
|||||
|---|---|---|---|---|---|
| SCAN | ESACF | ||||
| p+d | q | BIC | p+d | q | BIC |
| 0 | 1 | -2.3497 | 0 | 1 | -2.3497 |
| 1 | 1 | -2.32345 | |||
Copyright © SAS Institute, Inc. All Rights Reserved.