| The VARMAX Procedure |
| Vector Error Correction Modeling |
This section discusses the implication of cointegration for the autoregressive representation. Assume that the cointegrated series can be represented by a vector error correction model according to the Granger representation theorem (Engle and Granger 1987). Consider the vector autoregressive process with Gaussian errors defined by
 |
or
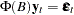 |
where the initial values, 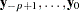 , are fixed and
, are fixed and 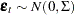 . Since the AR operator
. Since the AR operator 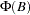 can be re-expressed as
can be re-expressed as 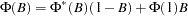 , where
, where 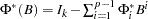 with
with 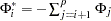 , the vector error correction model is
, the vector error correction model is
 |
or
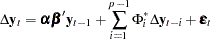 |
where 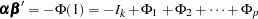 .
.
One motivation for the VECM( ) form is to consider the relation
) form is to consider the relation 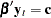 as defining the underlying economic relations and assume that the agents react to the disequilibrium error
as defining the underlying economic relations and assume that the agents react to the disequilibrium error 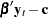 through the adjustment coefficient
through the adjustment coefficient  to restore equilibrium; that is, they satisfy the economic relations. The cointegrating vector,
to restore equilibrium; that is, they satisfy the economic relations. The cointegrating vector, 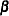 is sometimes called the long-run parameters.
is sometimes called the long-run parameters.
You can consider a vector error correction model with a deterministic term. The deterministic term 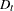 can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in the model.
can contain a constant, a linear trend, and seasonal dummy variables. Exogenous variables can also be included in the model.
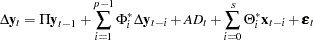 |
where  .
.
The alternative vector error correction representation considers the error correction term at lag 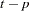 and is written as
and is written as
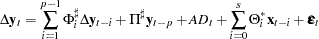 |
If the matrix  has a full-rank (
has a full-rank (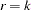 ), all components of
), all components of 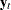 are
are 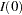 . On the other hand,
. On the other hand, 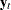 are stationary in difference if
are stationary in difference if 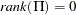 . When the rank of the matrix
. When the rank of the matrix  is
is  , there are
, there are  linear combinations that are nonstationary and
linear combinations that are nonstationary and  stationary cointegrating relations. Note that the linearly independent vector
stationary cointegrating relations. Note that the linearly independent vector 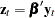 is stationary and this transformation is not unique unless
is stationary and this transformation is not unique unless 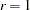 . There does not exist a unique cointegrating matrix
. There does not exist a unique cointegrating matrix 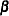 since the coefficient matrix
since the coefficient matrix  can also be decomposed as
can also be decomposed as
 |
where 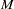 is an
is an 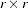 nonsingular matrix.
nonsingular matrix.
Test for the Cointegration
The cointegration rank test determines the linearly independent columns of  . Johansen (1988, 1995a) and Johansen and Juselius (1990) proposed the cointegration rank test by using the reduced rank regression.
. Johansen (1988, 1995a) and Johansen and Juselius (1990) proposed the cointegration rank test by using the reduced rank regression.
When you construct the VECM( ) form from the VAR(
) form from the VAR( ) model, the deterministic terms in the VECM(
) model, the deterministic terms in the VECM( ) form can differ from those in the VAR(
) form can differ from those in the VAR( ) model. When there are deterministic cointegrated relationships among variables, deterministic terms in the VAR(
) model. When there are deterministic cointegrated relationships among variables, deterministic terms in the VAR( ) model are not present in the VECM(
) model are not present in the VECM( ) form. On the other hand, if there are stochastic cointegrated relationships in the VAR(
) form. On the other hand, if there are stochastic cointegrated relationships in the VAR( ) model, deterministic terms appear in the VECM(
) model, deterministic terms appear in the VECM( ) form via the error correction term or as an independent term in the VECM(
) form via the error correction term or as an independent term in the VECM( ) form. There are five different specifications of deterministic trends in the VECM(
) form. There are five different specifications of deterministic trends in the VECM( ) form.
) form.
Case 1: There is no separate drift in the VECM(
 ) form.
) form. 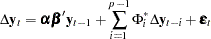
Case 2: There is no separate drift in the VECM(
 ) form, but a constant enters only via the error correction term.
) form, but a constant enters only via the error correction term. 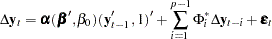
Case 3: There is a separate drift and no separate linear trend in the VECM(
 ) form.
) form. 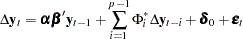
Case 4: There is a separate drift and no separate linear trend in the VECM(
 ) form, but a linear trend enters only via the error correction term.
) form, but a linear trend enters only via the error correction term. 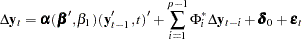
Case 5: There is a separate linear trend in the VECM(
 ) form.
) form. 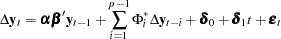
First, focus on Cases 1, 3, and 5 to test the null hypothesis that there are at most  cointegrating vectors. Let
cointegrating vectors. Let
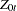 |
 |
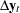 |
|||
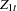 |
 |
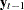 |
|||
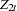 |
 |
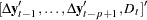 |
|||
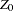 |
 |
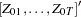 |
|||
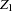 |
 |
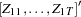 |
|||
 |
 |
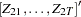 |
where 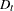 can be empty for Case 1, 1 for Case 3, and
can be empty for Case 1, 1 for Case 3, and 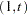 for Case 5.
for Case 5.
In Case 2,  and
and 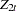 are defined as
are defined as
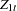 |
 |
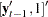 |
|||
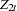 |
 |
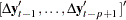 |
In Case 4,  and
and 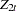 are defined as
are defined as
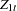 |
 |
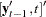 |
|||
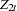 |
 |
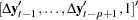 |
Let 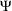 be the matrix of parameters consisting of
be the matrix of parameters consisting of 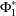 , ...,
, ..., 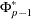 ,
,  , and
, and 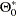 , ...,
, ..., 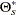 , where parameters
, where parameters  corresponds to regressors
corresponds to regressors 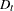 . Then the VECM(
. Then the VECM( ) form is rewritten in these variables as
) form is rewritten in these variables as
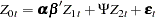 |
The log-likelihood function is given by
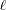 |
 |
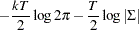 |
|||
 |
 |
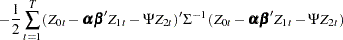 |
The residuals, 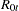 and
and 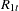 , are obtained by regressing
, are obtained by regressing 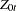 and
and  on
on 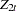 , respectively. The regression equation of residuals is
, respectively. The regression equation of residuals is
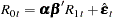 |
The crossproducts matrices are computed
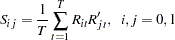 |
Then the maximum likelihood estimator for 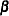 is obtained from the eigenvectors that correspond to the
is obtained from the eigenvectors that correspond to the  largest eigenvalues of the following equation:
largest eigenvalues of the following equation:
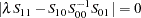 |
The eigenvalues of the preceding equation are squared canonical correlations between 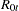 and
and 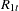 , and the eigenvectors that correspond to the
, and the eigenvectors that correspond to the  largest eigenvalues are the
largest eigenvalues are the  linear combinations of
linear combinations of 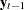 , which have the largest squared partial correlations with the stationary process
, which have the largest squared partial correlations with the stationary process 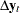 after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of
after correcting for lags and deterministic terms. Such an analysis calls for a reduced rank regression of 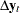 on
on 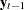 corrected for
corrected for 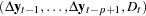 , as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are at most
, as discussed by Anderson (1951). Johansen (1988) suggests two test statistics to test the null hypothesis that there are at most  cointegrating vectors
cointegrating vectors
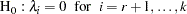 |
The trace statistic for testing the null hypothesis that there are at most  cointegrating vectors is as follows:
cointegrating vectors is as follows:
 |
The asymptotic distribution of this statistic is given by
 |
where 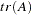 is the trace of a matrix
is the trace of a matrix  ,
, 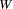 is the
is the  dimensional Brownian motion, and
dimensional Brownian motion, and 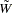 is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of deterministic trends in the vector error correction model.
is the Brownian motion itself, or the demeaned or detrended Brownian motion according to the different specifications of deterministic trends in the vector error correction model.
The maximum eigenvalue statistic for testing the null hypothesis that there are at most  cointegrating vectors is as follows:
cointegrating vectors is as follows:
 |
The asymptotic distribution of this statistic is given by
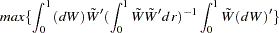 |
where 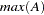 is the maximum eigenvalue of a matrix
is the maximum eigenvalue of a matrix  . Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
. Osterwald-Lenum (1992) provided detailed tables of the critical values of these statistics.
The following statements use the JOHANSEN option to compute the Johansen cointegration rank trace test of integrated order 1:
proc varmax data=simul2;
model y1 y2 / p=2 cointtest=(johansen=(normalize=y1));
run;
Figure 30.52 shows the output based on the model specified in the MODEL statement, an intercept term is assumed. In the "Cointegration Rank Test Using Trace" table, the column Drift In ECM means there is no separate drift in the error correction model and the column Drift In Process means the process has a constant drift before differencing. The "Cointegration Rank Test Using Trace" table shows the trace statistics based on Case 3 and the "Cointegration Rank Test Using Trace under Restriction" table shows the trace statistics based on Case 2. The output indicates that the series are cointegrated with rank 1 because the trace statistics are smaller than the critical values in both Case 2 and Case 3.
| Cointegration Rank Test Using Trace | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | 5% Critical Value | Drift in ECM | Drift in Process |
| 0 | 0 | 0.4644 | 61.7522 | 15.34 | Constant | Linear |
| 1 | 1 | 0.0056 | 0.5552 | 3.84 | ||
| Cointegration Rank Test Using Trace Under Restriction | ||||||
|---|---|---|---|---|---|---|
| H0: Rank=r |
H1: Rank>r |
Eigenvalue | Trace | 5% Critical Value | Drift in ECM | Drift in Process |
| 0 | 0 | 0.5209 | 76.3788 | 19.99 | Constant | Constant |
| 1 | 1 | 0.0426 | 4.2680 | 9.13 | ||
Figure 30.53 shows which result, either Case 2 (the hypothesis H0) or Case 3 (the hypothesis H1), is appropriate depending on the significance level. Since the cointegration rank is chosen to be 1 by the result in Figure 30.52, look at the last row that corresponds to rank=1. Since the  -value is 0.054, the Case 2 cannot be rejected at the significance level 5%, but it can be rejected at the significance level 10%. For modeling of the two Case 2 and Case 3, see Figure 30.56 and Figure 30.57.
-value is 0.054, the Case 2 cannot be rejected at the significance level 5%, but it can be rejected at the significance level 10%. For modeling of the two Case 2 and Case 3, see Figure 30.56 and Figure 30.57.
Figure 30.54 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 3.
Using the NORMALIZE= option, the first low of the "Beta" table has 1. Considering that the cointegration rank is 1, the long-run relationship of the series is
 |
 |
 |
|||
 |
 |
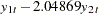 |
|||
 |
 |
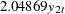 |
Figure 30.55 shows the estimates of long-run parameter (Beta) and adjustment coefficients (Alpha) based on Case 2.
Considering that the cointegration rank is 1, the long-run relationship of the series is
 |
 |
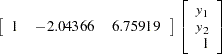 |
|||
 |
 |
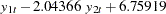 |
|||
 |
 |
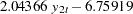 |
Estimation of Vector Error Correction Model
The preceding log-likelihood function is maximized for
 |
 |
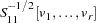 |
|||
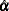 |
 |
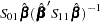 |
|||
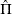 |
 |
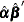 |
|||
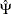 |
 |
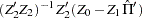 |
|||
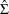 |
 |
 |
The estimators of the orthogonal complements of  and
and 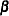 are
are
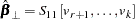 |
and
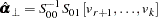 |
The ML estimators have the following asymptotic properties:
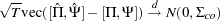 |
where
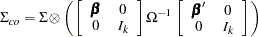 |
and
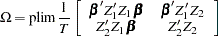 |
The following statements are examples of fitting the five different cases of the vector error correction models mentioned in the previous section.
For fitting Case 1,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1) noint;
For fitting Case 2,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend);
For fitting Case 3,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1);
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend)
trend=linear;
For fitting Case 5,
model y1 y2 / p=2 ecm=(rank=1 normalize=y1) trend=linear;
From Figure 30.53 that uses the COINTTEST=(JOHANSEN) option, you can fit the model by using either Case 2 or Case 3 because the test was not significant at the 0.05 level, but was significant at the 0.10 level. Here both models are fitted to show the difference in output display. Figure 30.56 is for Case 2, and Figure 30.57 is for Case 3.
For Case 2,
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1 ectrend)
print=(estimates);
run;
| Parameter Alpha * Beta' Estimates | |||
|---|---|---|---|
| Variable | y1 | y2 | 1 |
| y1 | -0.48015 | 0.98126 | -3.24543 |
| y2 | 0.12538 | -0.25624 | 0.84748 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.72759 | -0.77463 |
| y2 | 0.38982 | -0.55173 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -3.24543 | 0.33022 | 1, EC | ||
| AR1_1_1 | -0.48015 | 0.04886 | y1(t-1) | |||
| AR1_1_2 | 0.98126 | 0.09984 | y2(t-1) | |||
| AR2_1_1 | -0.72759 | 0.04623 | -15.74 | 0.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.77463 | 0.04978 | -15.56 | 0.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 0.84748 | 0.35394 | 1, EC | ||
| AR1_2_1 | 0.12538 | 0.05236 | y1(t-1) | |||
| AR1_2_2 | -0.25624 | 0.10702 | y2(t-1) | |||
| AR2_2_1 | 0.38982 | 0.04955 | 7.87 | 0.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.55173 | 0.05336 | -10.34 | 0.0001 | D_y2(t-1) | |
Figure 30.56 can be reported as follows:
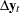 |
 |
 |
|||
 |
 |
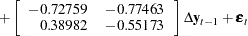 |
The keyword "EC" in the "Model Parameter Estimates" table means that the ECTREND option is used for fitting the model.
For fitting Case 3,
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1)
print=(estimates);
run;
| Parameter Alpha * Beta' Estimates | ||
|---|---|---|
| Variable | y1 | y2 |
| y1 | -0.46421 | 0.95103 |
| y2 | 0.17535 | -0.35923 |
| AR Coefficients of Differenced Lag | |||
|---|---|---|---|
| DIF Lag | Variable | y1 | y2 |
| 1 | y1 | -0.74052 | -0.76305 |
| y2 | 0.34820 | -0.51194 | |
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | -2.60825 | 1.32398 | -1.97 | 0.0518 | 1 |
| AR1_1_1 | -0.46421 | 0.05474 | y1(t-1) | |||
| AR1_1_2 | 0.95103 | 0.11215 | y2(t-1) | |||
| AR2_1_1 | -0.74052 | 0.05060 | -14.63 | 0.0001 | D_y1(t-1) | |
| AR2_1_2 | -0.76305 | 0.05352 | -14.26 | 0.0001 | D_y2(t-1) | |
| D_y2 | CONST2 | 3.43005 | 1.39587 | 2.46 | 0.0159 | 1 |
| AR1_2_1 | 0.17535 | 0.05771 | y1(t-1) | |||
| AR1_2_2 | -0.35923 | 0.11824 | y2(t-1) | |||
| AR2_2_1 | 0.34820 | 0.05335 | 6.53 | 0.0001 | D_y1(t-1) | |
| AR2_2_2 | -0.51194 | 0.05643 | -9.07 | 0.0001 | D_y2(t-1) | |
Figure 30.57 can be reported as follows:
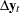 |
 |
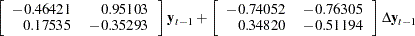 |
|||
 |
 |
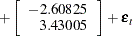 |
Test for the Linear Restriction on the Parameters
Consider the example with the variables 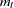 log real money,
log real money, 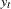 log real income,
log real income, 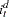 deposit interest rate, and
deposit interest rate, and 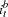 bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only
bond interest rate. It seems a natural hypothesis that in the long-run relation, money and income have equal coefficients with opposite signs. This can be formulated as the hypothesis that the cointegrated relation contains only 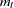 and
and 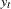 through
through 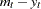 . For the analysis, you can express these restrictions in the parameterization of
. For the analysis, you can express these restrictions in the parameterization of 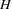 such that
such that 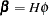 , where
, where 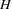 is a known
is a known  matrix and
matrix and 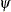 is the
is the 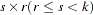 parameter matrix to be estimated. For this example,
parameter matrix to be estimated. For this example, 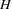 is given by
is given by
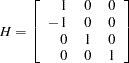 |
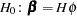
When the linear restriction 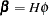 is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood estimator of
is given, it implies that the same restrictions are imposed on all cointegrating vectors. You obtain the maximum likelihood estimator of 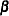 by reduced rank regression of
by reduced rank regression of 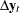 on
on 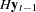 corrected for
corrected for 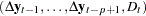 , solving the following equation
, solving the following equation
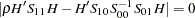 |
for the eigenvalues 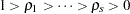 and eigenvectors
and eigenvectors 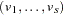 ,
,  given in the preceding section. Then choose
given in the preceding section. Then choose  that corresponds to the
that corresponds to the  largest eigenvalues, and the
largest eigenvalues, and the 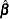 is
is 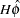 .
.
The test statistic for 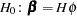 is given by
is given by
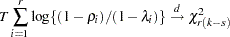 |
If the series has no deterministic trend, the constant term should be restricted by 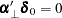 as in Case 2. Then
as in Case 2. Then 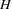 is given by
is given by
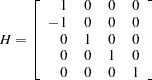 |
The following statements test that 2 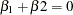 :
:
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1);
cointeg rank=1 h=(1,-2);
run;
Figure 30.58 shows the results of testing 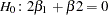 . The input
. The input 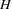 matrix is
matrix is  . The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null hypothesis.
. The adjustment coefficient is reestimated under the restriction, and the test indicates that you cannot reject the null hypothesis.
| Beta Under Restriction | |
|---|---|
| Variable | 1 |
| y1 | 1.00000 |
| y2 | -2.00000 |
| Alpha Under Restriction | |
|---|---|
| Variable | 1 |
| y1 | -0.47404 |
| y2 | 0.17534 |
| Hypothesis Test | |||||
|---|---|---|---|---|---|
| Index | Eigenvalue | Restricted Eigenvalue |
DF | Chi-Square | Pr > ChiSq |
| 1 | 0.4644 | 0.4616 | 1 | 0.51 | 0.4738 |
Test for the Weak Exogeneity and Restrictions of Alpha
Consider a vector error correction model:
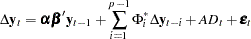 |
Divide the process 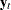 into
into 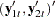 with dimension
with dimension 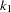 and
and 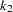 and the
and the  into
into
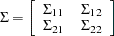 |
Similarly, the parameters can be decomposed as follows:
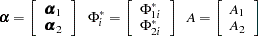 |
Then the VECM(p) form can be rewritten by using the decomposed parameters and processes:
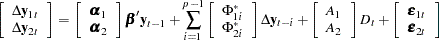 |
The conditional model for 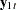 given
given 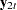 is
is
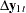 |
 |
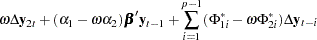 |
|||
 |
 |
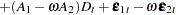 |
and the marginal model of 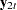 is
is
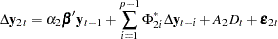 |
where 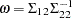 .
.
The test of weak exogeneity of 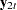 for the parameters
for the parameters 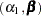 determines whether
determines whether 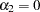 . Weak exogeneity means that there is no information about
. Weak exogeneity means that there is no information about 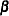 in the marginal model or that the variables
in the marginal model or that the variables 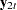 do not react to a disequilibrium.
do not react to a disequilibrium.
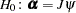
Consider the null hypothesis 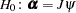 , where
, where  is a
is a 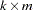 matrix with
matrix with 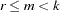 .
.
From the previous residual regression equation
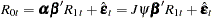 |
you can obtain
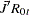 |
 |
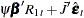 |
|||
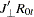 |
 |
 |
where 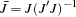 and
and 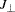 is orthogonal to
is orthogonal to  such that
such that 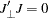 .
.
Define
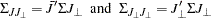 |
and let 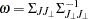 . Then
. Then 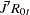 can be written as
can be written as
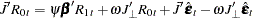 |
Using the marginal distribution of 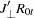 and the conditional distribution of
and the conditional distribution of 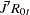 , the new residuals are computed as
, the new residuals are computed as
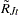 |
 |
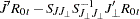 |
|||
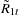 |
 |
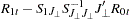 |
where
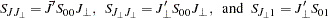 |
In terms of 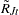 and
and 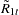 , the MLE of
, the MLE of 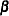 is computed by using the reduced rank regression. Let
is computed by using the reduced rank regression. Let
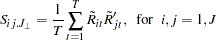 |
Under the null hypothesis 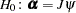 , the MLE
, the MLE 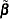 is computed by solving the equation
is computed by solving the equation
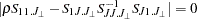 |
Then 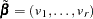 , where the eigenvectors correspond to the
, where the eigenvectors correspond to the  largest eigenvalues. The likelihood ratio test for
largest eigenvalues. The likelihood ratio test for 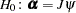 is
is
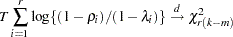 |
The test of weak exogeneity of 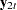 is a special case of the test
is a special case of the test 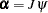 , considering
, considering 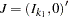 . Consider the previous example with four variables (
. Consider the previous example with four variables ( 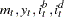 ). If
). If 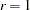 , you formulate the weak exogeneity of (
, you formulate the weak exogeneity of (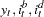 ) for
) for 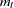 as
as 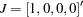 and the weak exogeneity of
and the weak exogeneity of 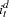 for (
for (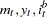 ) as
) as 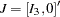 .
.
The following statements test the weak exogeneity of other variables, assuming 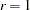 :
:
proc varmax data=simul2;
model y1 y2 / p=2 ecm=(rank=1 normalize=y1);
cointeg rank=1 exogeneity;
run;
Figure 30.59 shows that each variable is not the weak exogeneity of other variable.
| Testing Weak Exogeneity of Each Variables |
|||
|---|---|---|---|
| Variable | DF | Chi-Square | Pr > ChiSq |
| y1 | 1 | 53.46 | <.0001 |
| y2 | 1 | 8.76 | 0.0031 |
Forecasting of the VECM
Consider the cointegrated moving-average representation of the differenced process of 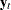
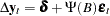 |
Assume that 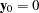 . The linear process
. The linear process 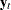 can be written as
can be written as
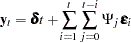 |
Therefore, for any 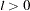 ,
,
 |
The 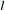 -step-ahead forecast is derived from the preceding equation:
-step-ahead forecast is derived from the preceding equation:
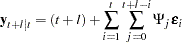 |
Note that
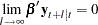 |
since 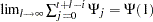 and
and 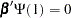 . The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error
. The long-run forecast of the cointegrated system shows that the cointegrated relationship holds, although there might exist some deviations from the equilibrium status in the short-run. The covariance matrix of the predict error  is
is
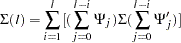 |
When the linear process is represented as a VECM( ) model, you can obtain
) model, you can obtain
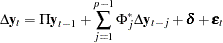 |
The transition equation is defined as
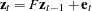 |
where 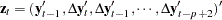 is a state vector and the transition matrix is
is a state vector and the transition matrix is
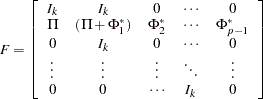 |
where 0 is a 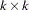 zero matrix. The observation equation can be written
zero matrix. The observation equation can be written
 |
where 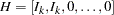 .
.
The 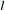 -step-ahead forecast is computed as
-step-ahead forecast is computed as
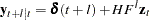 |
Cointegration with Exogenous Variables
The error correction model with exogenous variables can be written as follows:
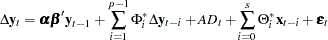 |
The following statements demonstrate how to fit VECMX(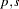 ), where
), where 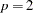 and
and 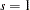 from the P=2 and XLAG=1 options:
from the P=2 and XLAG=1 options:
proc varmax data=simul3;
model y1 y2 = x1 / p=2 xlag=1 ecm=(rank=1);
run;
The following statements demonstrate how to BVECMX(2,1):
proc varmax data=simul3;
model y1 y2 = x1 / p=2 xlag=1 ecm=(rank=1)
prior=(lambda=0.9 theta=0.1);
run;
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.