Forecast Combination Model Specification Window

Once you have fit several forecasting models to a series, you face the question of which model to use to produce the final forecasts. One possible answer is to combine or average the forecasts from several models. Combining the predictions from several different forecasting methods is a popular approach to forecasting.

The way that you produce forecast combinations with the Time Series Forecasting System is to use the Forecast Combination Model Specification window to specify a new forecasting model that performs the averaging of forecasts from the models you want to combine. This new model is added to the list of fitted models just like other models. You can then use the Model Viewer window features and Model Fit Comparison window features to examine the fit of the combined model.

To specify a forecast combination model, select "Combine Forecasts" from the pop-up menu or toolbar, or select "Edit" and "Fit Model" from the menu bar. This brings up the Forecast Combination Model Specification window, as shown in Figure 39.29.

Figure 39.29 Forecast Combination Window

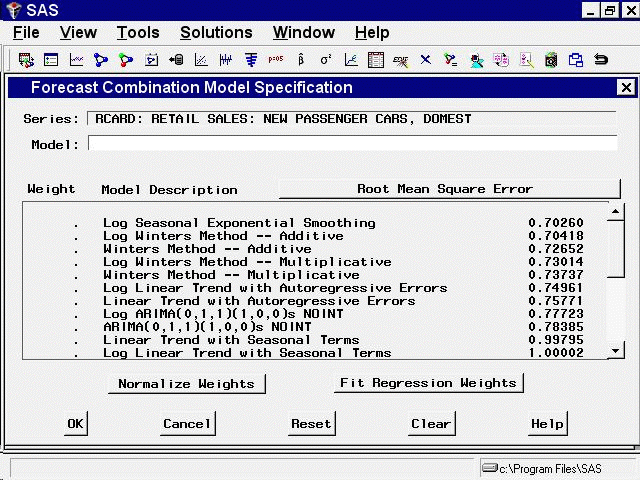
At the top of the Forecast Combination window is the name and label of the series and the label of the model you are specifying. The model label is filled in with an automatically generated label as you specify options. You can type over the automatic label with your own label for the model. To restore the automatic label, enter a blank label.

The middle part of the Forecast Combination window consists of the list of models that you have fit to the series. This table shows the label and goodness-of-fit measure for each model and the combining weight assigned to the model.

The Weight column controls how much weight is given to each model in the combined forecasts. A missing weight means that the model is not used. Initially, all the models have missing weight values.

You can enter the weight values you want to use in the Weight column. Alternatively, you can select models from the Model Description column, and weight values for the models you select are set automatically. To remove a model from the combination, select it again. This resets its weight value to missing.

At the bottom of the Forecast Combination window are two buttons: Normalize Weights and Fit Regression Weights. The Normalize Weights button adjusts the nonmissing weight values so that they sum to one. The Fit Regression Weights button uses linear regression to compute the weight values that produce the combination of model predictions with the best fit to the series.

If no models are selected, the Fit Regression Weights button fits weights for all the models in the list. You can compute regression weights for only some of the models by first selecting the models you want to combine and then selecting Fit Regression Weights. In this case, only the nonmissing Weight values are replaced with regression weights.

As an example of how to combine forecasting models, select all the models in the list. After you have finished selecting the models, all the models in the list should now have equal weight values, which implies a simple average of the forecasts.

Now select the Fit Regression Weights button. The system performs a linear regression of the series on the predictions from the models with nonmissing weight values and replaces the weight values with the estimated regression coefficients. These are the combining weights that produce the smallest mean square prediction error within the sample.

The Forecast Combination window should now appear as shown in Figure 39.30. (Note that some of the regression weight values are negative.)

Figure 39.30 Combining Models

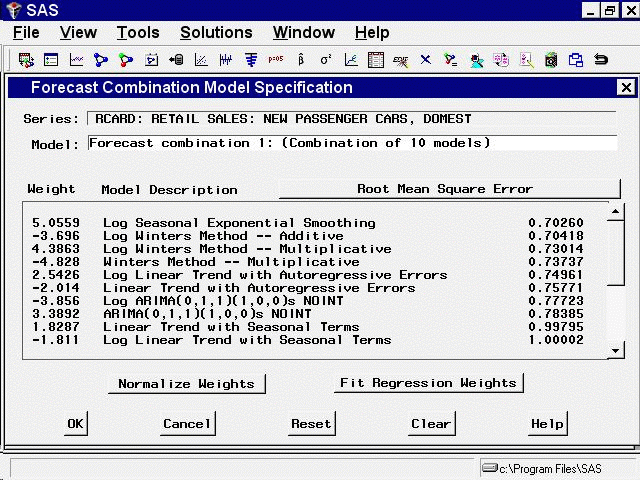
Select the OK button to fit the combined model. Now the Develop Models window shows this model to be the best fitting according to the root mean square error, as shown in Figure 39.31.

Figure 39.31 Develop Models Window Showing All Models Fit

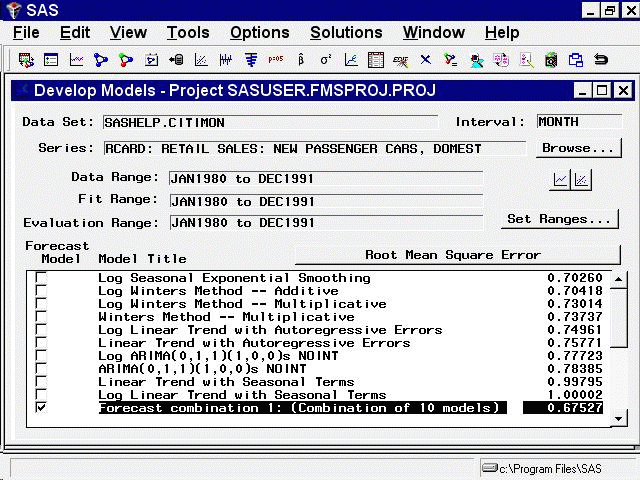
Notice that the combined model has a smaller root mean square error than any one of the models included in the combination. The confidence limits for forecast combinations are produced by taking a weighted average of the mean square prediction errors for the component forecasts, ignoring the covariance between the prediction errors.