| The SYSLIN Procedure |
| Two-Stage Least Squares Estimation |
In the supply and demand model, P is an endogenous variable, and consequently the OLS estimates are biased. The following example estimates this model using two-stage least squares.
proc syslin data=in 2sls;
endogenous p;
instruments y u s;
demand: model q = p y s;
supply: model q = p u;
run;
The 2SLS option in the PROC SYSLIN statement specifies the two-stage least squares method. The ENDOGENOUS statement specifies that P is an endogenous regressor for which first-stage predicted values are substituted. You need to declare an endogenous variable in the ENDOGENOUS statement only if it is used as a regressor; thus although Q is endogenous in this model, it is not necessary to list it in the ENDOGENOUS statement.
Usually, all predetermined variables that appear in the system are used as instruments. The INSTRUMENTS statement specifies that the exogenous variables Y, U, and S are used as instruments for the first-stage regression to predict P.
The 2SLS results are shown in Figure 26.3 and Figure 26.4. The first-stage regressions are not shown. To see the first-stage regression results, use the FIRST option in the PROC SYSLIN statement.
| Model | DEMAND |
|---|---|
| Dependent Variable | q |
| Label | Quantity |
| Model | SUPPLY |
|---|---|
| Dependent Variable | q |
| Label | Quantity |
| Analysis of Variance | |||||
|---|---|---|---|---|---|
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
| Model | 2 | 9.646109 | 4.823054 | 253.96 | <.0001 |
| Error | 57 | 1.082503 | 0.018991 | ||
| Corrected Total | 59 | 10.03724 | |||
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | DF | Parameter Estimate |
Standard Error | t Value | Pr > |t| | Variable Label |
| Intercept | 1 | -0.51878 | 0.490999 | -1.06 | 0.2952 | Intercept |
| p | 1 | 1.333080 | 0.059271 | 22.49 | <.0001 | Price |
| u | 1 | -1.14623 | 0.243491 | -4.71 | <.0001 | Unit Cost |
The 2SLS output is similar in form to the OLS output. However, the 2SLS results are based on predicted values for the endogenous regressors from the first stage instrumental regressions. This makes the analysis-of-variance table and the 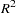 statistics difficult to interpret. See the sections ANOVA Table for Instrumental Variables Methods and The R-Square Statistics for details.
statistics difficult to interpret. See the sections ANOVA Table for Instrumental Variables Methods and The R-Square Statistics for details.
Note that, unlike the OLS results, the 2SLS estimate for the P coefficient in the demand equation (–1.115) is negative.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.