 |
|
| The SYSLIN Procedure |
| The R-Square Statistics |
As explained in the section ANOVA Table for Instrumental Variables Methods, when instrumental variables are used, the regression sum of squares (RSS) and the error sum of squares (ESS) do not sum to the total corrected sum of squares. In this case, there are several ways that the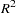 
statistic can be defined.
The definition of 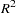used by the SYSLIN procedure is
 |
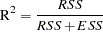This definition is consistent with the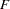 
test of the null hypothesis that the true coefficients of all regressors are zero. However, this 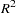might not be a good measure of the goodness of fit of the model.
System Weighted R-Square and System Weighted Mean Squared Error
The system weighted 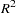, printed for the 3SLS, IT3SLS, SUR, ITSUR, and FIML methods, is computed as follows.
 |
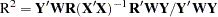In this equation, the matrix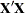 
is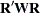 
and W is the projection matrix of the instruments:
 |
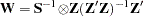The matrix Z is the instrument set, R is the regressor set, and S is the estimated cross-model covariance matrix.
The system weighted MSE, printed for the 3SLS, IT3SLS, SUR, ITSUR, and FIML methods, is computed as follows:
 |
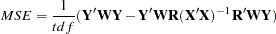In this equation, tdf is the sum of the error degrees of freedom for the equations in the system.
|
|
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.