| The MODEL Procedure |
| Profile Likelihood Confidence Intervals |
Wald-based and likelihood-ratio-based confidence intervals are available in the MODEL procedure for computing a confidence interval on an estimated parameter. A confidence interval on a parameter 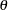 can be constructed by inverting a Wald-based or a likelihood-ratio-based test.
can be constructed by inverting a Wald-based or a likelihood-ratio-based test.
The approximate 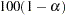 % Wald confidence interval for a parameter
% Wald confidence interval for a parameter 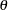 is
is
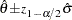 |
where 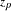 is the
is the 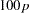 th percentile of the standard normal distribution,
th percentile of the standard normal distribution,  is the maximum likelihood estimate of
is the maximum likelihood estimate of 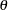 , and
, and 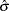 is the standard error estimate of
is the standard error estimate of  .
.
A likelihood-ratio-based confidence interval is derived from the 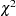 distribution of the generalized likelihood ratio test. The approximate
distribution of the generalized likelihood ratio test. The approximate  confidence interval for a parameter
confidence interval for a parameter 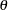 is
is
 |
where 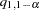 is the
is the  quantile of the
quantile of the 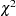 with one degree of freedom, and
with one degree of freedom, and 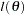 is the log likelihood as a function of one parameter. The endpoints of a confidence interval are the zeros of the function
is the log likelihood as a function of one parameter. The endpoints of a confidence interval are the zeros of the function  . Computing a likelihood-ratio-based confidence interval is an iterative process. This process must be performed twice for each parameter, so the computational cost is considerable. Using a modified form of the algorithm recommended by Venzon and Moolgavkar (1988), you can determine that the cost of each endpoint computation is approximately the cost of estimating the original system.
. Computing a likelihood-ratio-based confidence interval is an iterative process. This process must be performed twice for each parameter, so the computational cost is considerable. Using a modified form of the algorithm recommended by Venzon and Moolgavkar (1988), you can determine that the cost of each endpoint computation is approximately the cost of estimating the original system.
To request confidence intervals on estimated parameters, specify the PRL= option in the FIT statement. By default, the PRL option produces 95% likelihood ratio confidence limits. The coverage of the confidence interval is controlled by the ALPHA= option in the FIT statement.
The following is an example of the use of the confidence interval options.
data exp;
do time = 1 to 20;
y = 35 * exp( 0.01 * time ) + 5*rannor( 123 );
output;
end;
run;
proc model data=exp;
parm zo 35 b;
dert.z = b * z;
y=z;
fit y init=(z=zo) / prl=both;
test zo = 40.475437 ,/ lr;
run;
The output from the requested confidence intervals and the TEST statement are shown in Figure 18.56
| Nonlinear OLS Parameter Estimates | ||||
|---|---|---|---|---|
| Parameter | Estimate | Approx Std Err | t Value | Approx Pr > |t| |
| zo | 36.58933 | 1.9471 | 18.79 | <.0001 |
| b | 0.006497 | 0.00464 | 1.40 | 0.1780 |
Note that the likelihood ratio test reported the probability that 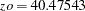 is 5% but
is 5% but 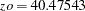 is the upper bound of a 95% confidence interval. To understand this conundrum, note that the TEST statement is using the likelihood ratio statistic to test the null hypothesis
is the upper bound of a 95% confidence interval. To understand this conundrum, note that the TEST statement is using the likelihood ratio statistic to test the null hypothesis  with the alternate that
with the alternate that  . The upper confidence interval can be viewed as a test with the null hypothesis
. The upper confidence interval can be viewed as a test with the null hypothesis 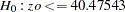 .
.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.