| The ENTROPY Procedure |
Example 12.3 Censored Data Models in PROC ENTROPY
Data available to an analyst might sometimes be censored, where only part of the actual series is observed. Consider the case in which only observations greater than some lower bound are recorded, as defined by the following process:
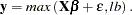 |
Running ordinary least squares estimation on data generated by the preceding process is not optimal because the estimates are likely to be biased and inefficient. One alternative to estimating models with censored data is the tobit estimator. This model is supported in the QLIM procedure in SAS/ETS and in the LIFEREG procedure in SAS/STAT. PROC ENTROPY provides another alternative which can make it very easy to estimate such a model correctly.
The following DATA step generates censored data in which any negative values of the dependent variable, y, are set to a lower bound of 0.
data cens;
do t = 1 to 100;
x1 = 5 * ranuni(456);
x2 = 10 * ranuni( 457);
y = 4.5*x1 + 2*x2 + 15 * rannor(458);
if( y<0 ) then y = 0;
output;
end;
run;
To illustrate the effect of the censored option in PROC ENTROPY, the model is initially estimated without accounting for censoring in the following statements:
title "Censored Data Estimation";
proc entropy data = cens gme primal;
priors intercept -32 32
x1 -15 15
x2 -15 15;
model y = x1 x2 /
esupports = (-25 1 25);
run;
| GME Variable Estimates | ||||
|---|---|---|---|---|
| Variable | Estimate | Approx Std Err | t Value | Approx Pr > |t| |
| x1 | 2.377609 | 0.000503 | 4725.98 | <.0001 |
| x2 | 2.353014 | 0.000255 | 9244.87 | <.0001 |
| intercept | 5.478121 | 0.00188 | 2906.41 | <.0001 |
The previous model is reestimated by using the CENSORED option in the following statements:
proc entropy data = cens gme primal;
priors intercept -32 32
x1 -15 15
x2 -15 15;
model y = x1 x2 /
esupports = (-25 1 25)
censored(lb = 0, esupports=(-15 1 15) );
run;
| GME Variable Estimates | ||||
|---|---|---|---|---|
| Variable | Estimate | Approx Std Err | t Value | Approx Pr > |t| |
| x1 | 4.429697 | 0.00690 | 641.85 | <.0001 |
| x2 | 1.46858 | 0.00349 | 420.61 | <.0001 |
| intercept | 8.261412 | 0.0259 | 319.51 | <.0001 |
The second set of entropy estimates are much closer to the true parameter estimates of 4.5 and 2. Since another alternative available for fitting a model of censored data is a tobit model, PROC QLIM is used in the following statements to fit a tobit model to the data:
proc qlim data=cens;
model y = x1 x2;
endogenous y ~ censored(lb=0);
run;
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 2.979455 | 3.824252 | 0.78 | 0.4359 |
| x1 | 1 | 4.882284 | 1.019913 | 4.79 | <.0001 |
| x2 | 1 | 1.374006 | 0.513000 | 2.68 | 0.0074 |
| _Sigma | 1 | 13.723213 | 1.032911 | 13.29 | <.0001 |
For this data and code, PROC ENTROPY produces estimates that are closer to the true parameter values than those computed by PROC QLIM.
Note: This procedure is experimental.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.