| The ENTROPY Procedure |
| BOUNDS Statement |
- BOUNDS bound1 <, bound2 ...> ;
The BOUNDS statement imposes simple boundary constraints on the parameter estimates. BOUNDS statement constraints refer to the parameters estimated by the ENTROPY procedure. You can specify any number of BOUNDS statements.
Each boundary constraint is composed of variables, constants, and inequality operators in the following form:
item operator item <,operator item <,operator item ...> >
Each item is a constant, the name of a regressor variable, or a list of regressor names. Each operator is <, >, <=, or >=.
You can use either the BOUNDS statement or the RESTRICT statement to impose boundary constraints; the BOUNDS statement provides a simpler syntax for specifying inequality constraints. See section RESTRICT Statement for more information about the computational details of estimation with inequality restrictions.
Lagrange multipliers are reported for all the active boundary constraints. In the printed output and in the OUTEST= data set, the Lagrange multiplier estimates are identified with the names BOUND1, BOUND2, and so forth. The probability of the Lagrange multipliers are computed using a beta distribution (LaMotte; 1994). Nonactive or nonbinding bounds have no effect on the estimation results and are not noted in the output. To give the constraints more descriptive names, use the RESTRICT statement instead of the BOUNDS statement.
The following BOUNDS statement constrains the estimates of the coefficients of WAGE and TARGET and the 10 coefficients of  through
through 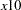 to be between zero and one. This example illustrates the use of parameter lists to specify boundary constraints.
to be between zero and one. This example illustrates the use of parameter lists to specify boundary constraints.
bounds 0 < wage target x1-x10 < 1;
The following is an example of the use of the BOUNDS statement to impose boundary constraints on the variables X1, X2, and X3:
proc entropy data=zero;
bounds .1 <= x1 <= 100,
0 <= x2 <= 25.6,
0 <= x3 <= 5;
model y = x1 x2 x3;
run;
The parameter estimates from this run are shown in Figure 12.23.
| Variables(Supports(Weights)) | x1 x2 x3 Intercept |
|---|---|
| Equations(Supports(Weights)) | y |
| Prior Distribution of Parameter T |
| Data Set Options | |
|---|---|
| DATA= | WORK.ZERO |
| Minimization Summary | |
|---|---|
| Parameters Estimated | 4 |
| Covariance Estimator | GME-NM |
| Entropy Type | Shannon |
| Entropy Form | Dual |
| Numerical Optimizer | Newton-Raphson |
| Final Information Measures | |
|---|---|
| Objective Function Value | 6.292861 |
| Signal Entropy | 6.375715 |
| Noise Entropy | -0.08285 |
| Normed Entropy (Signal) | 0.990364 |
| Normed Entropy (Noise) | 1.004172 |
| Parameter Information Index | 0.009636 |
| Error Information Index | -0.00417 |
Note: This procedure is experimental.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.