The HPPANEL Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names
Specifying the Input DataSpecifying the Regression ModelSpecifying the Number of Nodes and Number of ThreadsUnbalanced DataOne-Way Fixed-Effects ModelTwo-Way Fixed-Effects ModelBalanced PanelsUnbalanced PanelsOne-Way Random-Effects ModelTwo-Way Random-Effects ModelBetween EstimatorsPooled EstimatorLinear Hypothesis TestingSpecification TestsOUTPUT OUT= Data SetOUTEST= Data SetPrinted OutputODS Table Names -
Example

- References
Getting Started: HPPANEL Procedure
The following statements use the cost function data from Greene (1990) to estimate the variance components model. The variable Production is the log of output in millions of kilowatt-hours, and the variable Cost is the log of cost in millions of dollars. See Greene (1990) for details.
data greene; input firm year production cost @@; datalines; 1 1955 5.36598 1.14867 1 1960 6.03787 1.45185 1 1965 6.37673 1.52257 1 1970 6.93245 1.76627 2 1955 6.54535 1.35041 2 1960 6.69827 1.71109 2 1965 7.40245 2.09519 2 1970 7.82644 2.39480 3 1955 8.07153 2.94628 3 1960 8.47679 3.25967 ... more lines ...
You decide to fit the following model to the data,
![\[ C_{it}= \mr{Intercept} + {\bbeta }P_{it}+v_{i}+e_{t}+{\epsilon }_{it} \; \; \text {for }i=1, {\ldots }, \mi{N}\text { and }t=1, {\ldots }, \mi{T} \]](images/etshpug_hppanel0001.png)
where 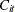 and
and 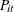 represent the cost and production; and
represent the cost and production; and 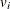 ,
, 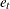 , and
, and 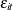 are the cross-sectional, time series, and error variance components, respectively.
are the cross-sectional, time series, and error variance components, respectively.
If you assume that the time and cross-sectional effects are random, four possible estimators are left for the variance components. The following statements choose the Fuller-Battese method to fit this model:
proc hppanel data=greene; model cost = production / rantwo vcomp = fb; id firm year; performance nodes=0 nthreads=2; run;
The output of the HPPANEL procedure is shown in Figure 7.1.
Figure 7.1: Two-Way Random Effects Results
Printed first is the model description, which reports the method used for estimation and the method used for estimating error components. Printed next is the fit statistics table, and then the variance components estimates. Finally, the table of regression parameter estimates shows the estimates, standard errors, and t tests.