The HPQLIM Procedure
The BAYES statement controls the Metropolis sampling scheme that is used to obtain samples from the posterior distribution of the underlying model and data.
-
DIAGNOSTICS=ALL | NONE | (keyword-list)
DIAG=ALL | NONE | (keyword-list) -
controls which diagnostics are produced. All the following diagnostics are produced when you specify DIAGNOSTICS=ALL. If you do not want any of these diagnostics, specify DIAGNOSTICS=NONE. If you want some but not all of the diagnostics, or if you want to change certain settings of these diagnostics, specify one or more of the following keywords. The default is DIAGNOSTICS=NONE.
- AUTOCORR <(LAGS=numeric-list)>
-
computes the autocorrelations at lags that are specified in the numeric-list. Elements in the numeric-list are truncated to integers, and repeated values are removed. If the LAGS= option is not specified, autocorrelations of lags 1, 5, and 10 are computed.
- ESS
-
computes Carlin’s estimate of the effective sample size, the correlation time, and the efficiency of the chain for each parameter.
- GEWEKE <(geweke-options)>
-
computes the Geweke spectral density diagnostics, which are essentially a two-sample t test between the first
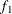 portion and the last
portion and the last 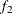 portion of the chain. The defaults are
portion of the chain. The defaults are 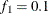 and
and 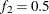 , but you can choose other fractions by using the following geweke-options:
, but you can choose other fractions by using the following geweke-options:
- HEIDELBERGER <(heidel-options)>
-
computes for each variable the Heidelberger and Welch diagnostic, which consists of a stationarity test of the null hypothesis that the sample values form a stationary process. If the stationarity test is not rejected, a halfwidth test is then carried out. Optionally, you can specify one or more of the following heidel-options:
-
MCSE
MCERROR -
computes the Monte Carlo standard error for each parameter. The Monte Carlo standard error, which measures the simulation accuracy, is the standard error of the posterior mean estimate and is calculated as the posterior standard deviation divided by the square root of the effective sample size.
- RAFTERY<(raftery-options)>
-
computes the Raftery and Lewis diagnostics, which evaluate the accuracy of the estimated quantile (
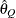 for a given
for a given 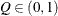 ) of a chain.
) of a chain. 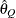 can achieve any degree of accuracy when the chain is allowed to run for a long time. The computation stops when the estimated
probability
can achieve any degree of accuracy when the chain is allowed to run for a long time. The computation stops when the estimated
probability 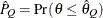 reaches within
reaches within 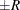 of the value
of the value 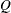 with probability
with probability 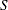 ; that is,
; that is, 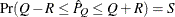 . The following raftery-options enable you to specify
. The following raftery-options enable you to specify 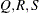 , and a precision level
, and a precision level  for the test:
for the test:
- QUANTILE | Q=value
-
specifies the order (a value between 0 and 1) of the quantile of interest. The default is 0.025.
- ACCURACY | R=value
-
specifies a small positive number as the margin of error for measuring the accuracy of the estimation of the quantile. The default is 0.005.
- PROBABILITY | S=value
-
specifies the probability of attaining the accuracy of the estimation of the quantile. The default is 0.95.
- EPSILON | EPS=value
-
specifies the tolerance level (a small positive number) for the stationary test. The default is 0.001.
- MINTUNE=number
-
specifies the minimum number of tuning phases. The default is 2.
- MAXTUNE=number
-
specifies the maximum number of tuning phases. The default is 24.
- NBI=number
-
specifies the number of burn-in iterations before the chains are saved. The default is 1,000.
- NMC=number
-
specifies the number of iterations after the burn-in. The default is 1,000.
- NTU=number
-
specifies the number of samples for each tuning phase. The default is 500.
- OUTPOST=SAS-data-set
-
names the SAS data set to contain the posterior samples. Alternatively, you can create the output data set by specifying an ODS OUTPUT statement as follows:
- PROPCOV=value
-
specifies the method that is used in constructing the initial covariance matrix for the Metropolis-Hastings algorithm. The QUANEW and NMSIMP methods find numerically approximated covariance matrices at the optimum of the posterior density function with respect to all continuous parameters. The tuning phase starts at the optimized values; in some problems, this can greatly increase convergence performance. If the approximated covariance matrix is not positive definite, then an identity matrix is used instead. You can specify the following values:
- CONGRA
-
performs a conjugate-gradient optimization.
- DBLDOG
-
performs a version of double-dogleg optimization.
- NEWRAP
-
performs a Newton-Raphson optimization that combines a line-search algorithm with ridging.
- NMSIMP
-
performs a Nelder-Mead simplex optimization.
- NRRIDG
-
performs a Newton-Raphson optimization with ridging.
- QUANEW
-
performs a quasi-Newton optimization.
- TRUREG
-
performs a trust-region optimization.
- SAMPLING=MULTIMETROPOLIS |UNIMETROPOLIS
-
specifies how to sample from the posterior distribution. SAMPLING=MULTIMETROPOLIS implements a Metropolis sampling scheme on a single block that contains all the parameters of the model. SAMPLING=UNIMETROPOLIS implements a Metropolis sampling scheme on multiple blocks, one for each parameter of the model. The default is SAMPLING=MULTIMETROPOLIS.
- SEED=number
-
specifies an integer seed in the range 1 to
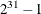 for the random number generator in the simulation. Specifying a seed enables you to reproduce identical Markov chains for
the same specification. If you do not specify the SEED= option, or if you specify a nonpositive seed, a random seed is derived
from the time of day.
for the random number generator in the simulation. Specifying a seed enables you to reproduce identical Markov chains for
the same specification. If you do not specify the SEED= option, or if you specify a nonpositive seed, a random seed is derived
from the time of day.
-
STATISTICS <(global-options)> = ALL | NONE | keyword | (keyword-list)
STATS <(global-options)> = ALL | NONE | keyword | (keyword-list) -
controls the number of posterior statistics that are produced. Specifying STATISTICS=ALL is equivalent to specifying STATISTICS=(CORR COV INTERVAL PRIOR SUMMARY). If you do not want any posterior statistics, specify STATISTICS=NONE. The default is STATISTICS=(SUMMARY INTERVAL). You can specify the following global-options:
- ALPHA=value <,value>…<,value>
-
controls the probabilities of the credible intervals. The value, which must be between 0 and 1, produces a pair of 100(1–value)% equal-tail and highest posterior density (HPD) intervals for each parameter. The default is ALPHA=0.05, which yields the 95% credible intervals for each parameter.
- PERCENT=value <,value>…<,value>
-
requests the percentile points of the posterior samples. The value must be between 0 and 100. The default is PERCENT=25, 50, 75, which yields the 25th, 50th, and 75th percentile points, respectively, for each parameter.
You can specify the following keywords:
- CORR
-
produces the posterior correlation matrix.
- COV
-
produces the posterior covariance matrix.
- INTERVAL
-
produces equal-tail credible intervals and HPD intervals. The default is to produce the 95% equal-tail credible intervals and 95% HPD intervals, but you can use the ALPHA= global-option to request intervals of any probabilities.
- NONE
-
suppresses printing of all summary statistics.
- PRIOR
-
produces a summary table of the prior distributions that are used in the Bayesian analysis.
- SUMMARY
-
produces the means, standard deviations, and percentile points (25th, 50th, and 75th) for the posterior samples. You can use the PERCENT= global-option to request specific percentile points.
-
THIN=number
THINNING=number -
controls the thinning of the Markov chain. Only one in every k samples is used when THIN=k. If NBI=
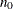 and NMC=n, the number of samples that are retained is
and NMC=n, the number of samples that are retained is
![\[ \biggl [ \frac{n_0+n}{k} \biggr ] - \biggl [ \frac{n_0}{k} \biggr ] \]](images/etshpug_hpqlim0039.png)
where [a] represents the integer part of the number a. The default is THIN=1.
