The HPQLIM Procedure

Tests on Parameters

In general, the tested hypothesis can be written as

$H_{0}: \mb{h} (\theta ) = 0$

where ${\mb{h} (\theta )}$ is an r $\times$ 1 vector-valued function of the parameters ${\theta }$ given by the r expressions that are specified in the TEST statement.

Let ${\hat{V}}$ be the estimate of the covariance matrix of ${\hat{\theta }}$ . Let ${\hat{\theta }}$ be the unconstrained estimate of ${\theta }$ and ${\tilde{\theta }}$ be the constrained estimate of ${\theta }$ such that ${h(\tilde{\theta }) = 0}$ . Let

$A(\theta ) = {{\partial } h(\theta )}/{{\partial } \theta }~ |_{\hat{\theta }}$

Using this notation, the test statistics for the three types of tests are computed as follows.

The Wald test statistic is defined as

$W = h^{'}(\hat{\theta })\big \lgroup { {A(\hat{\theta }) \hat{V} A^{'} (\hat{\theta })} }\big \rgroup ^{-1} h(\hat{\theta })$
The Lagrange multiplier test statistic is

$LM = {\lambda }^{'} A(\tilde{\theta }) \tilde{V} A^{'}(\tilde{\theta }) {\lambda }$

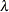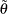where ${{\lambda }}$ is the vector of Lagrange multipliers from the computation of the restricted estimate ${\tilde{\theta }}$ .
The likelihood ratio test statistic is

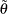$LR = 2 \left({L(\hat{\theta }) - L(\tilde{\theta })}\right)$

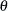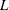where ${\tilde{\theta }}$ represents the constrained estimate of ${\theta }$ and ${L}$ is the concentrated log-likelihood value.

The following statements use the TEST statement to perform a likelihood ratio test:

   proc hpqlim;
      model y = x1 x2 x3;
      test x1 = 0, x2 * .5 + 2 * x3 = 0 /lr;
   run;

For more information, see the section Tests on Parameters in SAS/ETS 13.2 User's Guide.