PROC HPCOUNTREG Statement :: SAS/ETS(R) 13.2 User's Guide: High-Performance Procedures

Input Data Set Options

DATA=SAS-data-set: specifies the input SAS data set. If the DATA= option is not specified, PROC HPCOUNTREG uses the most recently created SAS data set.
GROUPID=variable: specifies an identification variable when a panel data model is estimated. The identification variable is used as a cross-sectional ID variable.

Output Data Set Options

OUTEST=SAS-data-set: writes the parameter estimates to the specified output data set.
CORROUT: writes the correlation matrix for the parameter estimates to the OUTEST= data set. This option is valid only if the OUTEST= option is specified.
COVOUT: writes the covariance matrix for the parameter estimates to the OUTEST= data set. This option is valid only if the OUTEST= option is specified.

Printing Options

You can specify the following options in either the PROC HPCOUNTREG statement or the MODEL statement:

CORRB: prints the correlation matrix of the parameter estimates.
COVB: prints the covariance matrix of the parameter estimates.
NOPRINT: suppresses all printed output.
PRINTALL: requests all printing options.

Estimation Control Options

You can specify the following options in either the PROC HPCOUNTREG statement or the MODEL statement:

COVEST=HESSIAN | OP | QML

specifies the type of covariance matrix for the parameter estimates.

The default is COVEST=HESSIAN. You can specify the following values:

HESSIAN: specifies the covariance from the Hessian matrix.
OP: specifies the covariance from the outer product matrix.
QML: specifies the covariance from the outer product and Hessian matrices.

Optimization Control Options

PROC HPCOUNTREG uses the nonlinear optimization (NLO) subsystem to perform nonlinear optimization tasks. You can specify the following options in either the PROC HPCOUNTREG statement or the MODEL statement.

ABSCONV=r ABSTOL=r

specifies an absolute function value convergence criterion by which minimization stops when 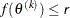$f(\theta ^{(k)})\leq \Argument{r}$ . The default value of r is the negative square root of the largest double-precision value, which serves only as a protection against overflows.

ABSFCONV=r ABSFTOL=r

specifies an absolute function difference convergence criterion by which minimization stops when the function value has a small change in successive iterations:

$|f(\theta ^{(k-1)}) - f(\theta ^{(k)})| \leq \Argument{r}$

The default is 0.

ABSGCONV=r ABSGTOL=r

specifies an absolute gradient convergence criterion. Optimization stops when the maximum absolute gradient element is small:

$\max _ j |g_ j(\theta ^{(k)})| \leq \Argument{r}$

The default is 1E–5.

ABSXCONV=r ABSXTOL=r

specifies an absolute parameter convergence criterion. Optimization stops when the Euclidean distance between successive parameter vectors is small:

$\parallel \theta ^{(k)} - \theta ^{(k-1)} \parallel _2 \leq \Argument{r}$

The default is 0.

FCONV=r FTOL=r

specifies a relative function convergence criterion. Optimization stops when a relative change of the function value in successive iterations is small:

${ \frac{ |f(\theta ^{(k)}) - f(\theta ^{(k-1)})|}{|f(\theta ^{(k-1)})|} } \leq \Argument{r}$

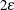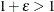The default value is $2 \epsilon$ , where $\epsilon$ denotes the machine precision constant, which is the smallest double-precision floating-point number such that $1 + \epsilon > 1$ .

GCONV=r GTOL=r

specifies a relative gradient convergence criterion. For all techniques except CONGRA, optimization stops when the normalized predicted function reduction is small:

$\frac{ g(\theta ^{(k)})^ T [H^{(k)}]^{-1} g(\theta ^{(k)})}{|f(\theta ^{(k)})| } \leq \Argument{r}$

For the CONGRA technique (where a reliable Hessian estimate 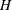$H$ is not available), the following criterion is used:

$\frac{ \parallel g(\theta ^{(k)}) \parallel _2^2 \quad \parallel s(\theta ^{(k)}) \parallel _2}{\parallel g(\theta ^{(k)}) - g(\theta ^{(k-1)}) \parallel _2 |f(\theta ^{(k)})| } \leq \Argument{r}$

The default is 1E–8.

MAXFUNC=i MAXFU=i

specifies the maximum number of function calls in the optimization process. The default is 1,000.

The optimization can terminate only after completing a full iteration. Therefore, the number of function calls that are actually performed can exceed the number of calls that are specified by this option.

MAXITER=i MAXIT=i

specifies the maximum number of iterations in the optimization process. The default is 200.

MAXTIME=r

specifies an upper limit of r seconds of CPU time for the optimization process. The default value is the largest floating-point double representation of your computer. The time that is specified by this option is checked only once at the end of each iteration. Therefore, the actual run time can be much longer than r. The actual run time includes the remaining time needed to finish the iteration and the time needed to generate the output of the results.

METHOD=value

specifies the iterative minimization method to use. The default is METHOD=NEWRAP. You can specify the following values:

CONGRA: specifies the conjugate-gradient method.
DBLDOG: specifies the double-dogleg method.
NEWRAP: specifies the Newton-Raphson method (this is the default).
NONE: specifies that no optimization be performed beyond using the ordinary least squares method to compute the parameter estimates.
NRRIDG: specifies the Newton-Raphson Ridge method.
QUANEW: specifies the quasi-Newton method.
TRUREG: specifies the trust region method.

SINGULAR=r

specifies the general singularity criterion that is applied by the HPCOUNTREG procedure in sweeps and inversions. The default is 1E–8.

The HPCOUNTREG Procedure