The HPCOUNTREG Procedure

Zero-Inflated Poisson Regression

Subsections:

In the zero-inflated Poisson (ZIP) regression model, the data generation process that is referred to earlier as Process 2 is

\[ g(y_{i}) = \frac{\exp (-\mu _{i})\mu _{i}^{y_{i}}}{y_{i}!} \]

where $\mu _ i=e^{\mathbf{x}_{i}'\bbeta }$. Thus the ZIP model is defined as

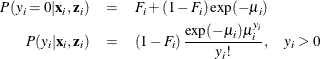
\begin{eqnarray*} P(y_{i}=0|\mathbf{x}_{i},\mathbf{z}_{i}) & =& F_{i} + \left(1 - F_{i}\right)\exp (-\mu _{i}) \\ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) & =& \left(1- F_{i} \right)\frac{\exp (-\mu _{i}) \mu _ i^{y_{i}}}{y_{i}!},\quad y_{i}>0 \end{eqnarray*}

The conditional expectation and conditional variance of $y_{i}$ are given by

\[ E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = \mu _{i}(1 -F_{i}) \]
\[ V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) = E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})(1+\mu _{i}F_{i}) \]

Note that the ZIP model (in addition to the ZINB model) exhibits overdispersion because $V(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) >E(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i})$.

In general, the log-likelihood function of the ZIP model is

\[ \mathcal{L} = \sum _{i=1}^{N}\ln \left[ P(y_{i}|\mathbf{x}_{i},\mathbf{z}_{i}) \right] \]

After a specific link function (either logistic or standard normal) for the probability $\varphi _{i}$ is chosen, it is possible to write the exact expressions for the log-likelihood function and the gradient.

ZIP Model with Logistic Link Function

First, consider the ZIP model in which the probability $\varphi _{i}$ is expressed by a logistic link function, namely

\[ \varphi _{i}=\frac{\exp (\mathbf{z}_{i}'\bgamma )}{1+\exp (\mathbf{z}_{i}'\bgamma )} \]

The log-likelihood function is

\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} } \ln \left[\exp (\mathbf{z}_{i}’\bgamma )+\exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right] \\ & & + \sum _{\{ i: y_{i}>0\} }\left[y_{i} \mathbf{x}_{i}’\bbeta -\exp (\mathbf{x}_{i}’\bbeta ) - \sum _{k=2}^{y_{i}}\ln (k) \right] \\ & & - \sum _{i=1}^{N}\ln \left[ 1 + \exp (\mathbf{z}_{i}’\bgamma ) \right] \end{eqnarray*}

ZIP Model with Standard Normal Link Function

Next, consider the ZIP model in which the probability $\varphi _{i}$ is expressed by a standard normal link function: $\varphi _{i}= \Phi (\mathbf{z}_{i}’\bgamma )$. The log-likelihood function is

\begin{eqnarray*} \mathcal{L} & = & \sum _{\{ i: y_{i}=0\} } \ln \left\{ \Phi (\mathbf{z}_{i}’\bgamma ) + \left[ 1- \Phi (\mathbf{z}_{i}’\bgamma )\right] \exp (-\exp (\mathbf{x}_{i}’\bbeta )) \right\} \\ & + & \sum _{\{ i: y_{i}>0\} } \left\{ \ln \left[ \left( 1-\Phi (\mathbf{z}_{i}’\bgamma )\right) \right] - \exp (\mathbf{x}_{i}’\bbeta ) + y_{i} \mathbf{x}_{i}’\bbeta - \sum _{k=2}^{y_{i}} \ln (k) \right\} \end{eqnarray*}

For more information about the zero-inflated Poisson regression model, see the section Zero-Inflated Poisson Regression in SAS/ETS 13.2 User's Guide.