The HPQLIM Procedure

OUTPUT Statement

OUTPUT OUT=SAS-data-set <output-options> ;

The OUTPUT statement creates a new SAS data set to contain variables that are specified with the COPYVAR option and the following data if they are specified by output-options: estimates of 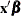$\mathbf{x^\prime }\bbeta$ , predicted value, residual, marginal effects, probability, standard deviation of the error, expected value, conditional expected value, technical efficiency measures, and inverse Mills ratio. When the response values are missing for the observation, all output estimates except the residual are still computed as long as none of the explanatory variables are missing. This enables you to compute these statistics for prediction. You can specify only one OUTPUT statement.

You must specify the OUT= option:

OUT=SAS-data-set: names the output data set.
COPYVAR=SAS-variable-names COPYVARS=(SAS-variable-names): adds SAS variables to the output data set

You can specify one or more of the following output-options:

CONDITIONAL: outputs estimates of conditional expected values of continuous endogenous variables.
ERRSTD: outputs estimates of 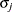$\sigma _ j$ , the standard deviation of the error term.
EXPECTED: outputs estimates of expected values of continuous endogenous variables.
MARGINAL: outputs marginal effects.
MILLS: outputs estimates of inverse Mills ratios of censored or truncated continuous, binary discrete, and selection endogenous variables.
PREDICTED: outputs estimates of predicted endogenous variables.
PROB: outputs estimates of probability of discrete endogenous variables taking the current observed responses.
PROBALL: outputs estimates of probability of discrete endogenous variables for all possible responses.
RESIDUAL: outputs estimates of residuals of continuous endogenous variables.
XBETA: outputs estimates of 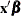$\mathbf{x^\prime }\bbeta$ .
TE1: outputs estimates of technical efficiency for each producer in the stochastic frontier model that is suggested by Battese and Coelli (1988).
TE2: outputs estimates of technical efficiency for each producer in the stochastic frontier model that is suggested by Jondrow et al. (1982).