Archimedean Copulas :: SAS/ETS(R) 13.1 User's Guide: High-Performance Procedures

Overview of Archimedean Copulas

Let function $\phi : [0,1] \rightarrow [0, \infty )$ be a strict Archimedean copula generator function, and suppose that its inverse $\phi ^{-1}$ is completely monotonic on $[0, \infty )$ . A strict generator is a decreasing function $\phi :[0,1]\rightarrow [0, \infty )$ that satisfies $\phi (0)=\infty$ and $\phi (1)=0$ . A decreasing function $f(t):[a,b]\rightarrow (-\infty ,\infty )$ is completely monotonic if it satisfies

$(-1)^ k \frac{d^ k}{dt^ k} f(t)\ge 0, k\in \mathbb {N}, t\in (a,b)$

An Archimedean copula is defined as follows:

$C(u_1, u_2,\ldots , u_ m) = \phi ^{-1}\Bigl ( \phi (u_1) + \cdots + \phi (u_ m) \Bigr )$

The Archimedean copulas available in the HPCOPULA procedure are the Clayton copula, the Frank copula, and the Gumbel copula.

Clayton Copula

Let the generator function $\phi (u) = { \theta }^{-1} \left(u^{-\theta } -1\right)$ . A Clayton copula is defined as

$C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \left[ \sum _{i=1}^ m u_ i^{-\theta } - m+1\right] ^{-1/\theta }$

where $\theta > 0$ .

Frank Copula

Let the generator function be

$\phi (u) = - \log \left[ \frac{\exp (-{\theta }u)-1}{\exp (-{\theta })-1}\right]$

A Frank copula is defined as

$C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \frac{1}{\theta } \log \left\{ 1 + \frac{\prod _{i=1}^{m}[\exp (-{\theta }u_ i)-1]}{[\exp (-{\theta })-1]^{m-1}} \right\}$

where $\theta \in (-\infty ,\infty ) \backslash \{ 0\}$ for $m=2$ and $\theta >0$ for $m\ge 3$ .

Gumbel Copula

Let the generator function $\phi (u) = (-\log u) ^{\theta }$ . A Gumbel copula is defined as

$C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \exp \left\{ - \left[ \sum _{i=1}^{m}(-\log u_ i)^\theta \right] ^{1/{\theta }} \right\}$

where $\theta > 1$ .

Simulation

Suppose that the generator of the Archimedean copula is $\phi$ . Then the simulation method that uses a Laplace-Stieltjes transformation of the distribution function is given by Marshall and Olkin (1988), where $\tilde{F}(t)= \int _0^\infty e^{-t x}dF(x)$ :

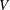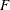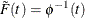Generate a random variable $V$ that has the distribution function $F$ such that $\tilde{F}(t)= \phi ^{-1}(t)$ .
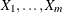Draw samples from the independent uniform random variables $X_1,\ldots , X_ m$ .
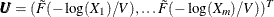Return $\bm U= (\tilde{F}(-\log (X_1)/V),\ldots \tilde{F}(-\log (X_ m)/V))^ T$ .

The Laplace-Stieltjes transformations are as follows:

For the Clayton copula, 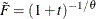$\tilde{F}= (1+t)^{-1/\theta }$ , and the distribution function 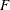$F$ is associated with a gamma random variable that has a shape parameter of 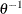$\theta ^{-1}$ and a scale parameter of 1.
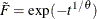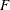For the Gumbel copula, $\tilde{F} = \exp (-t^{1/\theta })$ , and $F$ is the distribution function of the stable variable 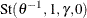$\textrm{St}(\theta ^{-1},1,\gamma ,0)$ , where $\gamma = [\cos (\pi /(2\theta ))]^\theta$ .
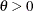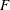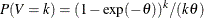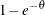For the Frank copula where $\theta >0$ , $\tilde{F}= - \log \{ 1-\exp (-t)[1- \exp (-\theta )]\} /\theta$ , and ${F}$ is a discrete probability function $P(V=k)=(1-\exp (-\theta ))^ k/(k\theta )$ . This probability function is related to a logarithmic random variable that has a parameter value of $1-e^{-\theta }$ .

For more information about simulating a random variable from a stable distribution, see Theorem 1.19 in Nolan (2010). For more information about simulating a random variable from a logarithmic series, see Chapter 10.5 in Devroye (1986).

For a Frank copula where $m=2$ and $\theta <0$ , the simulation can be done through conditional distributions as follows:

Draw independent $v_1,v_2$ from a uniform distribution.
Let $u_1= v_1$ .
Let $u_2 = -\frac1\theta \log \left(1+\frac{v_2(1-e^{-\theta })}{v_2(e^{-\theta v_1}-1)-e^{-\theta v_1}}\right)$ .

The HPCOPULA Procedure (Experimental)