Normal Copula :: SAS/ETS(R) 13.1 User's Guide: High-Performance Procedures

Normal Copula

Subsections:

Simulation

Let $u_ j \sim U(0,1)$ for $j=1,\ldots ,m$ , where $U(0,1)$ represents the uniform distribution on the $[0,1]$ interval. Let $\Sigma$ be the correlation matrix, where $m(m-1)/2$ parameters satisfy the positive semidefiniteness constraint. The normal copula can be written as

$\begin{equation*} C_{\Sigma }(u_1, u_2,{\ldots } u_ m) = \bm {\Phi }_\Sigma \Bigl (\Phi ^{-1} (u_1),{\ldots } \Phi ^{-1} (u_ m)\Bigr ) \end{equation*}$

where $\Phi$ is the distribution function of a standard normal random variable and $\bm {\Phi }_\Sigma$ is the $m$ -variate standard normal distribution with mean vector $0$ and covariance matrix $\Sigma$ . That is, the distribution $\bm {\Phi }_\Sigma$ is $N_ m(0,\Sigma )$ .

Simulation

For the normal copula, the input of the simulation is the correlation matrix $\Sigma$ . The normal copula can be simulated by the following steps, in which $\bm U= (U_1,\ldots ,U_ m)$ denotes one random draw from the copula:

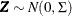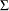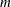Generate a multivariate normal vector $\bm Z \sim N(0,\Sigma )$ , where $\Sigma$ is an $m$ -dimensional correlation matrix.
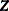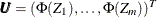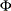Transform the vector $\bm Z$ into $\bm U= (\Phi (Z_1),\ldots ,\Phi (Z_ m))^ T$ , where $\Phi$ is the distribution function of univariate standard normal.

The first step can be achieved by Cholesky decomposition of the correlation matrix $\Sigma =LL^ T$ , where $L$ is a lower triangular matrix with positive elements on the diagonal. If $\bm {\tilde{Z}} \sim N(0,I)$ , then $L\bm {\tilde{Z}} \sim N(0,\Sigma )$ .

The HPCOPULA Procedure (Experimental)

Normal Copula

Simulation