The HPCDM Procedure (Experimental)

Simulation of Adjusted Compound Distribution Sample

Subsections:

Using Severity Adjustment Variables
Aggregate Adjusted Loss Simulation for a Multi-entity Scenario
Illustration of Aggregate Adjusted Loss Simulation Process
Randomizing the Order of Severity Draws across Observations of a Scenario

If you specify programming statements that adjust the severity value, then a separate adjusted compound distribution sample is also generated.

Your programming statements are expected to implement an adjustment function $f$ that uses the unadjusted severity value, $X_ j$ , to compute and return an adjusted severity value, $X_ j^ a$ . To compute $X_ j^ a$ , you might also use the sum of unadjusted severity values and the sum of adjusted severity values.

Formally, if $N$ denotes the number of loss events that are to be simulated for the current replication of the simulation process, then for the severity draw, $X_ j$ , of the $j$ th loss event ( $j=1, \ldots , N$ ), the adjusted severity value is

$X_ j^ a = f(X_ j, S_{j-1}, S_{j-1}^ a)$

where $S_{j-1} = \sum _{l=1}^{j-1} X_ l$ is the aggregate unadjusted loss before $X_ j$ is generated and $S_{j-1}^ a = \sum _{l=1}^{j-1} X_ l^ a$ is the aggregate adjusted loss before $X_ j$ is generated. The initial values of both types of aggregate losses are set to 0. In other words, $S_0 = 0$ and $S_0^ a = 0$ .

The aggregate adjusted loss for the replication is $S_ N^ a$ , which is denoted by $S^ a$ for simplicity, and is defined as

$S^ a = \sum _{j=1}^{N} X_ j^ a$

In your programming statements that implement $f$ , you can use the following keywords as placeholders for the input arguments of the function $f$ :

_SEV_: indicates the placeholder for $X_ j$ , the unadjusted severity value. PROC HPCDM generates this value as described in the section Simulation with No Regressors and No External Counts (step 2) or the section Simulation with Regressors and No External Counts (step 3). PROC HPCDM supplies this value to your program.
_CUMSEV_: indicates the placeholder for $S_{j-1}$ , the sum of unadjusted severity values that PROC HPCDM generates before $X_ j$ is generated. PROC HPCDM supplies this value to your program.
_CUMADJSEV_: indicates the placeholder for $S_{j-1}^ a$ , the sum of adjusted severity values that are computed by your programming statements before $X_ j$ is generated and adjusted. PROC HPCDM supplies this value to your program.

In your programming statements, you must assign the value of $X_ j^ a$ , the output of function $f$ , to a symbol that you specify in the ADJUSTEDSEVERITY= option in the PROC HPCDM statement. PROC HPCDM uses the final assigned value of this symbol as the value of $X_ j^ a$ .

You can use most DATA step statements and functions in your program. The DATA step file and the data set I/O statements (for example, INPUT, FILE, SET, and MERGE) are not available. However, some functionality of the PUT statement is supported. For more information, see the section “PROC FCMP and DATA Step Differences” in Base SAS Procedures Guide.

The simulation process that generates the aggregate adjusted loss sample is identical to the process that is described in the section Simulation with Regressors and No External Counts or the section Simulation with External Counts, except that after making each of the $N$ severity draws, PROC HPCDM executes your severity adjustment programming statements to compute the adjusted severity ( $X_ j^ a$ ). All the $N$ adjusted severity values are added to compute $S^ a$ , which forms a point of the aggregate adjusted loss sample. The process is illustrated using an example in the section Illustration of Aggregate Adjusted Loss Simulation Process.

Using Severity Adjustment Variables

If you do not specify the DATA= data set, then your ability to adjust the severity value is limited, because you can use only the current severity draw, sums of unadjusted and adjusted severity draws that are made before the current draw, and some constant numbers to encode your adjustment policy. That is sufficient if you want to estimate the distribution of aggregate adjusted loss for only one entity. However, if you are simulating a scenario that contains more than one entity, then it might be more useful if the adjustment policy depends on factors that are specific to each entity that you are simulating. To do that, you must specify the DATA= data set and encode such factors as adjustment variables in the DATA= data set. Let $A$ denote the set of values of the adjustment variables. Then, the form of the adjustment function $f$ that computes the adjusted severity value becomes

$X_ j^ a = f(X_ j, S_{j-1}, S_{j-1}^ a, A)$

PROC HPCDM reads the values of adjustment variables from the DATA= data set and supplies the set of those values ( $A$ ) to your severity adjustment program. For an invocation of $f$ with an unadjusted severity value of $X_ j$ , the values in set $A$ are read from the same observation that is used to simulate $X_ j$ .

All adjustment variables that you use in your program must be present in the DATA= data set. You must not use any keyword for a placeholder symbol as a name of any variable in the DATA= data set, whether the variable is a severity adjustment variable or a regressor in the frequency or severity model. Further, the following restrictions apply to the adjustment variables:

You can use only numeric-valued variables in PROC HPCDM programming statements. This restriction also implies that you cannot use SAS functions or call routines that require character-valued arguments, unless you pass those arguments as constant (literal) strings or characters.
You cannot use functions that create lagged versions of a variable in PROC HPCDM programming statements. If you need lagged versions, then you can use a DATA step before the PROC HPCDM step to add those versions to the input data set.

The use of adjustment variables is illustrated using an example in the section Illustration of Aggregate Adjusted Loss Simulation Process.

Aggregate Adjusted Loss Simulation for a Multi-entity Scenario

If you are simulating a scenario that consists of multiple entities, then you can use some additional pieces of information in your severity adjustment program. Let the scenario consist of $K$ entities and let $N_ k$ denote the number of loss events that are incurred by $k$ th entity ( $k = 1, \ldots , K$ ) in the current iteration of the simulation process. The total number of severity draws that need to be made is $N = \sum _{k=1}^ K N_ k$ . The aggregate adjusted loss is now defined as

$S^ a = \sum _{k=1}^{K} \sum _{j=1}^{N_ k} X_{k,j}^ a$

where $X_{k,j}^ a$ is an adjusted severity value of the $j$ th draw ( $j=1, \ldots , N_ k$ ) for the $k$ th entity, and the form of the adjustment function $f$ that computes $X_{k,j}^ a$ is

$X_{k,j}^ a = f(X_{k,j}, S_{k,j-1}, S_{k,j-1}^ a, S_{n-1}, S_{n-1}^ a, A)$

where $X_{k,j}$ is the value of the $j$ th draw of unadjusted severity for the $k$ th entity. $S_{k,j-1} = \sum _{l=1}^{j-1} X_{k,l}$ and $S_{k,j-1}^ a = \sum _{l=1}^{j-1} X_{k,l}^ a$ are the aggregate unadjusted loss and the aggregate adjusted loss, respectively, for the $k$ th entity before $X_{k,j}$ is generated. The index $n$ ( $n = 1, \ldots , N$ ) keeps track of the total number of severity draws, across all entities, that are made before $X_{k,j}$ is generated. So $S_{n-1} = \sum _{l=1}^{n-1} X_ l$ and $S_{n-1}^ a = \sum _{l=1}^{n-1} X_ l^ a$ are the aggregate unadjusted loss and aggregate adjusted loss, respectively, for all the entities that are processed before $X_{k,j}$ is generated. Note that $S_{n-1}$ and $S_{n-1}^ a$ include the $j-1$ draws that are made for the $k$ th entity before $X_{k,j}$ is generated.

The initial values of all types of aggregate losses are set to 0. In other words, $S_0 = 0$ , $S_0^ a = 0$ , and for all values of $k$ , $S_{k,0} = 0$ and $S_{k,0}^ a = 0$ .

PROC HPCDM uses the final value that you assign to the ADJUSTEDSEVERITY= symbol in your programming statements as the value of $X_{k,j}^ a$ .

In your severity adjustment program, you can use the following two additional placeholder keywords:

_CUMSEVFOROBS_: indicates the placeholder for $S_{k,j-1}$ , which is the total loss that is incurred by the $k$ th entity before the current loss event. PROC HPCDM supplies this value to your program.
_CUMADJSEVFOROBS_: indicates the placeholder for $S_{k,j-1}^ a$ , which is the total adjusted loss that is incurred by the $k$ th entity before the current loss event. PROC HPCDM supplies this value to your program.

The previously described placeholder symbols _CUMSEV_ and _CUMADJSEV_ represent $S_{n-1}$ and $S_{n-1}^ a$ , respectively. If you have only one entity in the scenario ( $K=1$ ), then the values of _CUMSEVFOROBS_ and _CUMADJSEVFOROBS_ are identical to the values of _CUMSEV_ and _CUMADJSEV_, respectively.

There is one caveat when a scenario consists of more than one entity ( $K > 1$ ) and when you use any of the symbols for cumulative severity values (_CUMSEV_, _CUMADJSEV_, _CUMSEVFOROBS_, or _CUMADJSEVFOROBS_) in your programming statements. In this case, to make the simulation realistic, it is important to randomize the order of $N$ severity draws across $K$ entities. For more information, see the section Randomizing the Order of Severity Draws across Observations of a Scenario.

Illustration of Aggregate Adjusted Loss Simulation Process

This section continues the example in the section Simulation with Regressors and No External Counts to illustrate the simulation of aggregate adjusted loss.

Recall that the earlier example simulates a scenario that consists of five policyholders. Assume that you want to compute the distribution of the aggregate amount paid to all the policyholders in a year, where the payment for each loss is decided by a deductible and a per-payment limit. To begin with, you must record the deductible and limit information in the input DATA= data set. The following table shows the DATA= data set from the earlier example, extended to include two variables, Deductible and Limit:

Obs     age     gender  carType  deductible  limit
1       30      2       1        250         5000
2       25      1       2        500         3000
3       45      2       2        100         2000
4       33      1       1        500         5000
5       50      1       1        200         2000

The variables Deductible and Limit are referred to as severity adjustment variables, because you need to use them to compute the adjusted severity. Let AmountPaid represent the value of adjusted severity that you are interested in. Further, let the following SAS programming statements encode your logic of computing the value of AmountPaid:

    amountPaid = MAX(_sev_ - deductible, 0);
    amountPaid = MIN(amountPaid, MAX(limit - _cumadjsevforobs_, 0));

PROC HPCDM supplies your program with values of the placeholder symbols _SEV_ and _CUMADJSEVFOROBS_, which represent the value of the current unadjusted severity draw and the sum of adjusted severity values from the previous draws, respectively, for the observation that is being processed. The use of _CUMADJSEVFOROBS_ helps you ensure that the payment that is made to a given policyholder in a year does not exceed the limit that is recorded in the Limit variable.

In order to simulate a sample for the aggregate of AmountPaid, you need to submit a PROC HPCDM step whose structure is like the following:

proc hpcdm data=<data set name> adjustedseverity=amountPaid 
       severityest=<severity parameter estimates data set>
       countstore=<count model store>;
    severitymodel <severity distribution name(s)>;
    
    amountPaid = MAX(_sev_ - deductible, 0);
    amountPaid = MIN(amountPaid, MAX(limit - _cumadjsevforobs_, 0));
run;

The simulation process of one replication that generates one point of the aggregate loss sample and the corresponding point of the aggregate adjusted loss sample is as follows:

Use the values Age=30, Gender=2, and CarType=1 in the first observation to draw a count from the count distribution. Let that count be 3. Repeat the process for the remaining four observations. Let the counts be as shown in the Count column in the following table:
```
Obs     age     gender  carType  deductible  limit   count
1       30      2       1        250         5000    2
2       25      1       2        500         3000    1
3       45      2       2        100         2000    2
4       33      1       1        500         5000    3
5       50      1       1        200         2000    0
```
Note that the Count column is shown for illustration only; it is not added as a variable to the DATA= data set.
The simulated counts from all the observations are added to get a value of 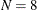$N=8$ . This means that for this particular replication, you expect a total of eight loss events in a year from these five policyholders.
For the first observation, the scale parameter of the severity distribution is computed by using the values Age=30, Gender=2, and CarType=1. That value of the scale parameter is used together with estimates of the other parameters from the SEVERITYEST= data set to make two draws from the severity distribution. The process is repeated for the remaining four policyholders. The fifth policyholder does not generate any loss event for this particular replication, so no severity draws are made by using the fifth observation. Let the severity draws, rounded to integers for convenience, be as shown in the _SEV_ column in the following table, where the _SEV_ column is shown for illustration only; it is not added as a variable to the DATA= data set:
```
Obs     age     gender  carType  deductible  limit   count   _sev_
1       30      2       1        250         5000    2       350  2100 
2       25      1       2        500         3000    1       4500
3       45      2       2        100         2000    2       700  4300
4       33      1       1        200         5000    3       600  1500  950
5       50      1       1        200         2000    0
```
The sample point for the aggregate unadjusted loss is computed by adding the severity values of eight draws, which gives an aggregate loss value of 15,000. The unadjusted aggregate loss is also referred to as the ground-up loss.

For each of the severity draws, your severity adjustment programming statements are executed to compute the adjusted severity, which is the value of AmountPaid in this case. For the draws in the preceding table, the values of AmountPaid are as follows:
```
Obs     deductible  limit   _sev_    _cumadjsevforobs_   amountPaid
1       250         5000    350      0                   100        
1       250         5000    2100     100                 1850       
2       500         3000    4500     0                   3000       
3       100         2000    700      0                   600        
3       100         2000    4300     600                 1400       
4       200         5000    600      0                   400        
4       200         5000    1500     400                 1300        
4       200         5000    950      1700                750          
```
The adjusted severity values are added to compute the cumulative payment value of 9,400, which forms the first sample point for the aggregate adjusted loss.

After recording the aggregate unadjusted and aggregate adjusted loss values in their respective samples, the process returns to step 1 to compute the next sample point unless the specified number of sample points have been simulated.

In this particular example, you can verify that the order in which the 8 loss events are simulated does not affect the aggregate adjusted loss. As a simple example, consider the following order of draws that is different from the consecutive order that was used in the preceding table:
```
Obs     deductible  limit   _sev_    _cumadjsevforobs_   amountPaid
4       200         5000    600      0                   400        
3       100         2000    4300     0                   2000
1       250         5000    350      0                   100        
3       100         2000    700      2000                0        
4       200         5000    950      400                 750          
1       250         5000    2100     100                 1850       
2       500         3000    4500     0                   3000
4       200         5000    1500     1150                1300        
```
Although the payments that are made for individual loss events differ, the aggregate adjusted loss is still 9,400.

However, in general, when you use a cumulative severity value such as _CUMADJSEVFOROBS_ in your program, the order in which the draws are processed affects the final value of aggregate adjusted loss. For more information, see the sections Randomizing the Order of Severity Draws across Observations of a Scenario and Illustration of the Need to Randomize the Order of Severity Draws.

Randomizing the Order of Severity Draws across Observations of a Scenario

If you specify a scenario that consists of a group of more than one entity, then it is assumed that each entity generates its loss events independently from other entities. In other words, the time at which the loss event of one entity is generated or recorded is independent of the time at which the loss event of another entity is generated or recorded. If entity $k$ generates $N_ k$ loss events, then the total number of loss events for a group of $K$ entities is $N = \sum _{k=1}^ K N_ k$ . To simulate the aggregate loss for this group, $N$ severity draws are made and aggregated to compute one point of the compound distribution sample. However, to honor the assumption of independence among entities, the order of those $N$ severity draws must be randomized across $K$ entities such that no entity is preferred over another.

The $K$ entities are represented by $K$ observations of the scenario in the DATA= data set. If you specify external counts, the $K$ observations correspond to the observations that have the same replication identifier value. If you do not specify the external counts, then the $K$ observations correspond to all the observations in the BY group or in the entire DATA= set if you do not specify the BY statement.

The randomization process over $K$ observations is implemented as follows. First, one of the $K$ observations is chosen at random and one severity value is drawn from the severity distribution implied by that observation, then another observation is chosen at random and one severity value is drawn from its implied severity distribution, and so on. In each step, the total number of events that are simulated for the selected observation $k$ is incremented by 1. When all $N_ k$ events for an observation $k$ are simulated, observation $k$ is retired and the process continues with the remaining observations until a total of $N$ severity draws are made. Let $k(j)$ denote a function that implements this randomization by returning an observation $k$ ( $k = 1, \ldots , K$ ) for the $j$ th draw ( $j=1, \ldots , N$ ). The aggregate loss computation can then be formally written as

$S = \sum _{j=1}^{N} X_{k(j)}$

where $X_{k(j)}$ denotes the severity value that is drawn by using observation $k(j)$ .

If you do not specify a scale regression model for severity, then all severity values are drawn from the same severity distribution. However, if you specify a scale regression model for severity, then the severity draw is made from the severity distribution that is determined by the values of regressors in observation $k$ . In particular, the scale parameter of the distribution depends on the values of regressors in observation $k$ . If $R(l)$ denotes the scale regression model for observation $l$ and $X_{R(l)}$ denotes the severity value drawn from scale regression model $R(l)$ , then the aggregate loss computation can be formally written as

$S = \sum _{j=1}^{N} X_{R(k(j))}$

This randomization process is especially important in the context of simulating an adjusted compound distribution sample when your severity adjustment program uses the aggregate adjusted severity observed so far to adjust the next severity value. For an illustration of the need to randomize in such cases, see the next section.

Illustration of the Need to Randomize the Order of Severity Draws

This section uses the example of the section Illustration of Aggregate Adjusted Loss Simulation Process, but with the following PROC HPCDM step:

proc hpcdm data=<data set name> adjustedseverity=amountPaid 
       severityest=<severity parameter estimates data set> 
       countstore=<count model store>;
    severitymodel <severity distribution name(s)>;
    
    if (_cumadjsev_ > 15000) then
        amountPaid = 0;
    else do;
        penaltyFactor = MIN(3, 15000/(15000 - _cumadjsev_));
        amountPaid = MAX(0, _sev_ - deductible * penaltyFactor);
    end;
run;

The severity adjustment statements in the preceding steps compute the value of AmountPaid by using the following provisions in the insurance policy:

There is a limit of 15,000 on the total amount that can be paid in a year to the group of policyholders that is being simulated. The amount of payment for each loss event depends on the total amount of payments before that loss event.
The penalty for incurring more losses is imposed in the form of an increased deductible. In particular, the deductible is increased by the ratio of the maximum cumulative payment (15,000) to the amount that remains available to pay for future losses in the year. The factor by which the deductible can be raised has a limit of three.

This example illustrates only step 3 of the simulation process, where randomization is done. It assumes that step 2 of the simulation process is identical to the step 2 in the example in the section Illustration of Aggregate Adjusted Loss Simulation Process. At the beginning of step 3, let the severity draws from all the observations be as shown in the _SEV_ column in the following table:

Obs     age     gender  carType  deductible  count   _sev_
1       30      2       1        250         2       350  2100 
2       25      1       2        500         1       4500
3       45      2       2        100         2       700  4300
4       33      1       1        200         3       600  1500  950
5       50      1       1        200         0

If the order of these eight draws is not randomized, then all the severity draws for the first observation are adjusted before all the severity draws of the second observation, and so on. The execution of the severity adjustment program leads to the following sequence of values for AmountPaid:

Obs     deductible  _sev_  _cumadjsev_  penaltyFactor  amountPaid
1       250         350    0            1              100            
1       250         2100   100          1.0067         1848.32         
2       500         4500   1948.32      1.1493         3925.36         
3       100         700    5873.68      1.6436         535.64          
3       100         4300   6409.32      1.7461         4125.39         
4       200         600    10534.72     3              0               
4       200         1500   10534.72     3              900             
4       200         950    11434.72     3              350

The preceding sequence of simulating loss events results in a cumulative payment of 11,784.72.

If the sequence of draws is randomized over observations, then the computation of the cumulative payment might proceed as follows for one instance of randomization:

Obs     deductible  _sev_  _cumadjsev_  penaltyFactor  amountPaid
2       500         4500   0            1              4000
1       250         350    4000         1.3636         9.09
3       100         700    4009.09      1.3648         563.52
4       200         950    4572.61      1.4385         662.30
4       200         1500   5234.91      1.5361         1192.78         
1       250         2100   6427.69      1.7498         1662.54         
4       200         600    8090.24      2.1708         165.83          
3       100         4300   8256.07      2.2242         4077.58

In this example, a policyholder is identified by the value in the Obs column. As the table indicates, PROC HPCDM randomizes the order of loss events not only across policyholders but also across the loss events that a given policyholder incurs. The particular sequence of loss events that is shown in the table results in a cumulative payment of 12,333.65. This differs from the cumulative payment that results from the previously considered nonrandomized sequence of loss events, which tends to penalize the fourth policyholder by always processing her payments after all other payments, with a possibility of underestimating the total paid amount. This comparison not only illustrates that the order of randomization affects the aggregate adjusted loss sample but also corroborates the arguments about the importance of order randomization that are made at the beginning of the section Randomizing the Order of Severity Draws across Observations of a Scenario.