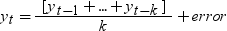Modeling and Forecasting Task

About the Modeling and Forecasting Task
Example: Creating a Random Walk Model for the SASHELP.PRICEDATA Data Set
Assigning Data to Roles
Setting the Model Options
Random Walk
Moving Average
Exponential Smoothing
ARIMA
ARIMAX
Unobserved Components
Setting the Forecasting Options
Setting the Output Options

About the Modeling and Forecasting Task

The Modeling and Forecasting task creates forecasting models that use your time series data. This task requires data in a valid time series format. To create this data, use the Time Series Data Preparation task before running the Modeling and Forecasting task.

Example: Creating a Random Walk Model for the SASHELP.PRICEDATA Data Set

To create this example:
  1. In the Tasks section, expand the Forecasting folder and double-click Modeling and Forecasting. The user interface for the Modeling and Forecasting task opens.
  2. On the Data tab, select the SASHELP.PRICEDATA data set.
  3. Assign columns to these roles and specify these options:
    Role
    Column
    Roles
    Dependent variable
    sale
    Additional Roles
    Time ID
    date
    Properties
    Season length
    12
  4. Click the Model tab, and select these options:
    • From the Forecasting model type drop-down list, select Random walk.
    • Under the Model settings heading, select the Drift and Seasonal check boxes.
  5. To run the task, click Submit SAS Code.
The results show the Random Walk model for the Sashelp.Pricedata data set.
Random Walk Model for Sashelp.Pricedata Data Set

Assigning Data to Roles

To run the Modeling and Forecasting task, you must assign a column to the Dependent variable role, and you must specify a forecasting model type on the Model tab.
Roles and Options
Description
Roles
Dependent variable
specifies the dependent variable.
Additional Roles
Time ID
specifies the column that contains the time ID values.
Properties
Interval
shows the interval for the time ID variable. For more information about SAS time intervals, see Understanding SAS Time Intervals.
Note: This value is determined by the input data set. You cannot change this value in the Modeling and Forecasting task.
Multiplier
shows the multiplier for the time interval. By default, the multiplier is 1.
Note: This value is determined by the input data set. You cannot change this value in the Modeling and Forecasting task.
Shift
shows the shift for the time interval. By default, the shift is 1.
Note: This value is determined by the input data set. You cannot change this value in the Modeling and Forecasting task.
Season length
specifies the seasonality of the time interval. The default value depends on the time interval.
Additional Roles
Season length
enables you to specify the seasonality of the data when you do not assign a time ID variable.
Group analysis by
lists the variable or variables that you want to use as the classification (BY) variables.

Setting the Model Options

To use the Modeling and Forecasting task, you must select a forecasting model type. You can choose from six model types: random walk, moving average, exponential smoothing, ARIMA, ARIMAX, and unobserved components.

Random Walk

To create a random walk model:
  1. From the Forecasting model type drop-down list, select Random walk.
  2. Select one of these types of random walk models:
    • Drift creates a Random Walk model with Drift, or in ARIMA notation ARIMA(0, 1, 0).
    • Trend .
    • Seasonal creates a Seasonal Random Walk model, or ARIMA(0, 1, 0)(0, 1, 0)s with no intercept.
  3. Under the Plots heading, select the plots to include in the results. You can choose from a variety of series plots, residual plots, and forecast plots.

Moving Average

The formula for the moving average model with width k is y sub t , equals . fraction left bracket . y sub t minus 1 end sub . plus dot dot dot plus . y sub t minus k end sub . right bracket , over k end fraction . plus e r r o r. Click image for alternative formats..
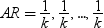In ARIMA notation, this model is ARIMA(k, 0, 0) with no intercept and with the autoregressive parameters (AR) fixed: eh r equals , 1 over k , comma , 1 over k , comma dot dot dot comma , 1 over k. Click image for alternative formats..
To create a moving average model:
  1. From the Forecasting model type drop-down list, select Moving average.
  2. In the Window (periods) box, specify the number of periods for the moving average. This value must be an integer greater than 0 and less than 14.
  3. Under the Plots heading, select the plots to include in the results. You can choose from a variety of series plots, residual plots, and forecast plots.

Exponential Smoothing

Exponential smoothing is a forecasting technique that uses exponentially declining weights to produce a weighted moving average of time series values. You can choose from several forecasting models.
To create an exponential smoothing model:
  1. From the Forecasting model type drop-down list, select Exponential smoothing.
  2. From the Forecasting model drop-down list, select the model that you want to use. You can choose from these models.
    • Simple (single) exponential smoothing, which is the default
    • Double (Brown) exponential smoothing
    • Linear (Holt) exponential smoothing
    • Damped trend exponential smoothing
    • Additive seasonal exponential smoothing
    • Multiplicative seasonal exponential smoothing
    • Winter additive model
  3. From the Transformation drop-down list, select the transformation to apply to the time series. By default, no transformation is applied. If you select the Box-Cox transformation, then you must specify a parameter value between -5 and 5 in the Box-Cox transformation parameter box.
  4. From the Forecast type drop-down list, specify whether the model uses the mean forecasts or the median forecasts.
  5. Under the Plots heading, select the plots to include in the results. You can choose from a variety of model plots, error plots, and forecast plots.

ARIMA

When you create an Autoregressive Integrated Moving Average (ARIMA) model, you can specify the autoregressive and moving average polynomials of an ARIMA model.
To create an ARIMA model:
  1. From the Forecasting model type drop-down list, select ARIMA.
  2. Under the ARIMA heading, specify the autoregressive, differencing, and moving average orders for the ARIMA model.
    Here are the options for the simple ARIMA:
    • Autoregressive order (p) specifies the simple autoregressive order. You can specify an integer from 0 to 13. The default value is 0.
    • Differencing order (d) specifies the simple differencing order. You can specify an integer from 0 to 13. The default value is 0.
    • Moving average order (q) specifies the simple moving average. You can specify an integer from 0 to 13. The default value is 0.
    Here are the options for the seasonal ARIMA:
    • Autoregressive order (P) specifies the seasonal autoregressive order. You can specify an integer from 0 to 5. The default value is 0.
    • Differencing order (D) specifies the simple differencing order. You can specify an integer from 0 to 3. The default value is 0.
    • Moving average order (Q) specifies the simple moving average. You can specify an integer from 0 to 5. The default value is 0.
  3. Specify whether to include the intercept in the model. The intercept is included by default.
  4. Under the Plots heading, select the plots to include in the results. You can choose from a variety of series plots, residual plots, and forecast plots.

ARIMAX

When you create an Autoregressive Integrated Moving Average (ARIMA) model, you can specify the autoregressive and moving average polynomials of an ARIMA model. In an ARIMAX model, you can also include independent variables in the model.
To create an ARIMAX model:
  1. From the Forecasting model type drop-down list, select ARIMAX.
  2. Under the ARIMA heading, specify the autoregressive, differencing, and moving average orders for the ARIMA model.
    Here are the options for the simple ARIMA:
    • Autoregressive order (p) specifies the simple autoregressive order. You can specify an integer from 0 to 13. The default value is 0.
    • Differencing order (d) specifies the simple differencing order. You can specify an integer from 0 to 13. The default value is 0.
    • Moving average order (q) specifies the simple moving average. You can specify an integer from 0 to 13. The default value is 0.
    Here are the options for the seasonal ARIMA:
    • Autoregressive order (P) specifies the seasonal autoregressive order. You can specify an integer from 0 to 5. The default value is 0.
    • Differencing order (D) specifies the simple differencing order. You can specify an integer from 0 to 3. The default value is 0.
    • Moving average order (Q) specifies the simple moving average. You can specify an integer from 0 to 5. The default value is 0.
  3. In the Independent variables role, assign the variables from the input data set that you want to include in the model.
  4. Specify whether to include the intercept in the model. The intercept is included by default.
  5. Under the Plots heading, select the plots to include in the results. You can choose from a variety of series plots, residual plots, and forecast plots.

Unobserved Components

To create an unobserved components model:
  1. From the Forecasting model type drop-down list, select Unobserved components.
  2. (Optional) To include independent variables in the model, expand the Regression Effects heading and select the Include independent variables check box. Assign the variables that you want to include in the model to the Independent variables role.
  3. To include an irregular component, expand the Irregular Component heading and select the Include an irregular component check box. An irregular component is included by default.
    The irregular component corresponds to the overall random error in the model. The initial variance is the value used as the initial value during the parameter estimation process. To change this value, select Specify variance and enter a different value. To keep this value as your initial variance, select Fix variance value.
  4. To include a trend component, expand the Trend Component heading. The level component and the slope component combine to define the trend component for the model. If you specify both a level and slope component, then a locally linear trend is obtained. If you omit the slope component, then a local level is used.
    1. To include a level component in the model, select the Include a level component check box. (The level component is included by default.) Then you can specify whether to change the initial variance (which is 0 by default) and whether to check for level breaks.
    2. To include a slope component in the model, select the Include a slope component check box. Then you can specify whether to change the initial variance (which is 0 by default).
  5. (Optional) To include a seasonal component, the season length must be greater than one. Expand the Seasonal Component heading and select the Include a seasonal component check box. Specify the type of seasonal component. A seasonal component can be one of two types: dummy or trigonometric. You can also specify whether to change the initial variance (which is 0 by default).
  6. (Optional) To include a cycle component, expand the Cycle Component heading and select the Include a cycle component check box. You can specify these options:
    • To specify an initial cycle period to use during the parameter estimation process, select the Specify cycle period check box. Then specify the initial value in the box. This value must be an integer greater than 2. By default, the initial value is 3.
    • To specify an initial damping factor to use during the parameter estimation process, select the Specify damping factor check box, and then specify the initial value in the box. You can specify any value between 0 and 1 (excluding 0 but including 1). By default, the initial value is 0.01.
    • To specify an initial value for the disturbance variance parameter that the task uses during the parameter estimation process, select the Specify variance check box. Then specify the initial value in the box. This value must be greater than or equal to 0. By default, the initial value is 0.
  7. Under the Plots heading, select the plots to include in the results. You can choose from a variety of residual plots, smoothed component estimates, filtered component estimates, and series decomposition and forecast plots.

Setting the Forecasting Options

Option
Description
Forecast Settings
Number of periods to forecast
specifies the number of periods into the future for which multistep forecasts are made. The larger the horizon value, the larger the prediction error variance at the end of the horizon. By default, the horizon is 12. Valid values are integers greater than or equal to 0 and less than 32,768.
Forecast confidence level
specifies the confidence level for the series. By default, this confidence level is 95% .
Number of periods to hold back
specifies a subset of actual time series values to hold back, starting from the end of the last nonmissing observation. Valid values are integers greater than or equal to 0 and less than 32,768.
Outlier Detection
Note: This option is not available if you selected Exponential smoothing as the forecasting model type.
Perform outlier detection
specifies that any outliers that are automatically detected during the creation of the model are inputs in the model.

Setting the Output Options

To create an output data set, click the Output tab. The types of output data sets that you can create depend on the forecasting model type.
Copyright © SAS Institute Inc. All rights reserved.