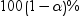Binary Logistic Regression Task

About the Binary Logistic Regression Task

Example: Classifying E-Mail as Junk

Assigning Data to Roles

Building a Model

Create a Main Effect

Create Crossed Effects (Interactions)

Create a Nested Effect

Create a Full Factorial Model

Create N-Way Factorial

Create Polynomial Effects of the Nth Order

Setting the Model Options

Specifying the Model Selection Options

Setting Options

Creating Output Data Sets

About the Binary Logistic Regression Task

The Binary Logistic Regression task is used to fit a logistic regression model to investigate the relationship between discrete responses with binary levels and a set of explanatory variables.

Note: You must have SAS/STAT to use this task.

Example: Classifying E-Mail as Junk

To create this example:

In the Tasks section, expand the Statistics folder and double-click Binary Logistic Regression. The user interface for the Binary Logistic Regression task opens.
On the Data tab, select the SASHELP.JUNKMAIL data set.

Assign columns to these roles and specify these options:

Role	Column Name
Response	Class
Event of interest	1
Continuous variables	Exclamation CapAvg

Click the Model tab. Select the Exclamation and CapAvg variables, and click Add.
To run the task, click .

Example of Results from Binary Logistic Regression Task

Assigning Data to Roles

To run the Binary Logistic Regression task, you must assign columns to the Response variable and a column to either the Classification variables role or the Continuous variables role.

Role	Description
Roles
Response
Response data consists of numbers of events and trials	specifies whether the response data consists of events and trials.
Number of events	specifies the variable that contains the number of events for each observation.
Number of trials	specifies the variable that contains the number of trials for each observation.
Response	specifies the variable that contains the response data. To perform a binary logistic regression, the response variable should have only two levels. Use the Event of interest drop-down list to select the event category for the binary response model.
Link function	specifies the link function that links the response probabilities to the linear predictors. Here are the valid values: Complementary log-log is the complementary log-log function. Probit is the inverse standard normal distribution function. Logit is the log odds function.
Explanatory Variables
Classification variables	specifies the classification variables to use in the analysis. A classification variable is a variable that enters the statistical analysis or model not through its values, but through its levels. The process of associating values of a variable with levels is termed levelization.
Parameterization of Effects
Coding	specifies the parameterization method for the classification variable. Design matrix columns are created from the classification variables according to the selected coding scheme. You can select from these coding schemes: Effects coding specifies effect coding. GLM coding specifies less-than-full-rank, reference-cell coding. This coding scheme is the default. Reference coding specifies reference-cell coding.
Treatment of Missing Values
An observation is excluded from the analysis when either of these conditions is met: if any variable in the model contains a missing value if any classification variable contains a missing value (regardless of whether the classification variable is used in the model)
Continuous variables	specifies the continuous variables to use as the explanatory variables in the analysis.
Additional Roles
Frequency count	specifies the variables that contain the frequency of occurrence for each observation. The task treats each observation as if it appears n times, where n is the value of the variable for that observation.
Weight variable	specifies the how much to weight each observation in the input data set.
Group analysis by	creates separate analyses based on the number of BY variables.

Building a Model

Create a Main Effect

Select the variable name in the Variables box.
Click Add to add the variable to the Model effects box.

Create Crossed Effects (Interactions)

Select two or more variables in the Variables box. To select more than one variable, press Ctrl.
Click Cross.

Create a Nested Effect

Nested effects are specified by following a main effect or crossed effect with a classification variable or list of classification variables enclosed in parentheses. The main effect or crossed effect is nested within the effects listed in parentheses. Here are examples of nested effects: B(A), C(B*A), D*E(C*B*A). In this example, B(A) is read "A nested within B."

Select the effect name in the Model effects box.
Click Nest. The Nested window opens.
Select the variable to use in the nested effect. Click Outer or Nested within Outer to specify how to create the nested effect.

Note: The Nested within Outer button is available only when a classification variable is selected.
Click Add.

Create a Full Factorial Model

Select two or more variables in the Variables box.
Click Full Factorial.

For example, if you select the Height, Weight, and Age variables and then click Full Factorial, these model effects are created: Age, Height, Weight, Age*Height, Age*Weight, Height*Weight, and Age*Height*Weight.

Create N-Way Factorial

Select two or more variables in the Variables box.
Click N-way Factorial to add these effects to the Model effects box.

For example, if you select the Height, Weight, and Age variables and then specify the value of N as 2, when you click N-way Factorial, these model effects are created: Age, Height, Weight, Age*Height, Age*Weight, and Height*Weight. If N is set to a value greater than the number of variables in the model, N is effectively set to the number of variables.

Create Polynomial Effects of the Nth Order

Select one variable in the Variables box.
Specify higher-degree crossings by adjusting the number in the N field.
Click Polynomial Order=N to add the polynomial effects to the Model effects box.

For example, if you select the Age and Height variables and then you specify 3 in the N field, when you click Polynomial Order=N, these model effects are created: Age, Age*Age, Age*Age*Age, Height, Height*Height, and Height*Height*Height.

Setting the Model Options

Option	Description
Model
Include an intercept in the model	specifies whether to include the intercept in the model.
Offset variable	specifies a variable to be used as an offset to the linear predictor. An offset plays the role of an effect whose coefficient is known to be 1. Observations that have missing values for the offset variable are excluded from the analysis.

Specifying the Model Selection Options

Option	Description
Model Selection
Selection method	specifies the model selection method for the model. The task performs model selection by examining whether effects should be added to or removed from the model according to the rules that are defined by the selection method. Here are the valid values for the selection methods: None fits the full model. Forward selection starts with no effects in the model and adds effects based on the Significance level to add an effect to the model option. Backward elimination starts with all the effects in the model and deletes effects based on the value in the Significance level to remove an effect from the model option.
Selection method (continued)	Fast backward elimination uses a computational algorithm of Lawless and Singhal (1978). This algorithm computes a first-order approximation to the remaining slope estimates for each subsequent elimination of a variable from the model. Variables are removed from the model based on these approximate estimates. This selection method is extremely efficient because the model is not refitted for every variable removed. Stepwise selection is similar to the forward selection model. However, effects that are already in the model do not necessarily stay there. Effects are added to the model based on the Significance level to add an effect to the model option and are removed from the model based on the Significance level to remove an effect from the model option. Stepwise selection with fast backward elimination uses a computational algorithm of Lawless and Singhal. This algorithm computes a first-order approximation to the remaining slope estimates for each subsequent elimination of a variable from the model. Variables are removed from the model based on these approximate estimates. This selection method is extremely efficient because the model is not refitted for every variable removed.
Details
Display selection process details	specifies how much information about the selection process to include in the results. You can choose to display a summary, details for each step of the selection process, or all of the information about the selection process.
Maintain hierarchy of effects	specifies how the model hierarchy requirement is applied and that only a single effect or multiple effects can enter or leave the model at one time. For example, suppose you specify the main effects A and B and the interaction AB in the model. In the first step of the selection process, either A or B can enter the model. In the second step, the other main effect can enter the model. The interaction effect can enter the model only when both main effects have already been entered. Also, before A or B can be removed from the model, the AB interaction must first be removed. Model hierarchy refers to the requirement that, for any term to be in the model, all effects contained in the term must be present in the model. For example, in order for the interaction AB to enter the model, the main effects A and B must be in the model. Likewise, neither effect A nor B can leave the model while the interaction AB is in the model.

Setting Options

Option Name	Description
Statistics Note: In addition to the default statistics that are included in the results, you can select the additional statistics to include.
Classification table	classifies the input binary response observations according to whether the predicted event probabilities are above or below the cut-point value z in the range. An observation is predicted as an event if the predicted event probability equals or exceeds z.
Partial correlation	computes the partial correlation statistic $open , beta sub i , close . square root of fraction chi sub i and super 2 , minus 2 , over negative 2 log of , l sub 0 end fraction end root. Click image for alternative formats.$ for each parameter i, where X²_i is the Wald chi-square statistic for the parameter and log L₀ is the log-likelihood of the intercept-only model (Hilbe 2009). If X²_i < 2, the partial correlation is set to 0.
Generalized R square	requests a generalized R square measure for the fitted model.
Goodness-of-fit and Overdispersion
Deviance and Pearson goodness-of-fit	specifies whether to calculate the deviance and Pearson goodness-of-fit.
Aggregate by	specifies the subpopulations on which the Pearson chi-square test statistic and the likelihood ratio chi-square test statistic (deviance) are calculated. Observations with common values in the given list of variables are regarded as coming from the same subpopulation. Variables in the list can be any variables in the input data set.
Correct for overdispersion	specifies whether to correct for overdispersion by using the Deviance or Pearson estimate.
Hosmer & Lemeshow goodness-of-fit	performs the Hosmer and Lemeshow goodness-of-fit test (Hosmer and Lemeshow 2000) for the case of a binary response model. The subjects are divided into approximately 10 groups of approximately the same size based on the percentiles of the estimated probabilities. The discrepancies between the observed and expected number of observations in these groups are summarized by the Pearson chi-square statistic. This statistic is then compared to a chi-square distribution with t degrees of freedom, where t is the number of groups minus n. By default, n = 2. A small p-value suggests that the fitted model is not an adequate model.
Multiple Comparisons
Perform multiple comparisons	specifies whether to compute and compare the least squares means of fixed effects.
Select the effects to test	specifies the effects that you want to compare. You specified these effects on the Model tab.
Method	requests a multiple comparison adjustment for the p-values and confidence limits for the differences of the least squares means. Here are the valid methods: Bonferroni, Nelson, Scheffé, Sidak, and Tukey.
Significance level	requests that a t type confidence interval be constructed for each of the least squares means with a confidence level of 1 – number. The value of number must be between 0 and 1. The default value is 0.05.
Exact Tests
Exact test of intercept	calculates the exact test for the intercept.
Select effects to test	calculates exact tests of the parameters for the selected effects.
Significance level	specifies the level of significance for confidence limits for the parameters or odds ratios.
Parameter Estimates
You can calculate these parameter estimates: standardized estimates exponentiated estimates correlations of parameter estimates covariances of parameter estimates You can specify the confidence intervals for parameters, confidence intervals for odds ratios, and the confidence level for these estimates.
Diagnostics
Influence diagnostics	displays the diagnostic measures for identifying influential observations. For each observation, the results include the sequence number of the observation, the values of the explanatory variables included in the final model, and the regression diagnostic measures developed by Pregibon (1981). You can specify whether to include the standardized and likelihood residuals in the results.
Plots
You can select whether to include plots in the results. Here are the additional plots that you can include in the results: standardized DFBETA by observation number influence statistics by observation number influence on model fit and parameter estimates predicted probability plots effect plot odds ratio plot ROC plot You can specify whether to display these plots in a panel or individually.
Label influence and ROC plots	specifies the variable from the input data that contains the labels for the influence and ROC plots.
Maximum number of plot points	specifies the maximum number of points to include in the plots. By default, 5,000 points are shown.
Methods
Optimization
Method	specifies the optimization technique for estimating the regression parameters. The Fisher scoring and Newton-Raphson algorithms yield the same estimates, but the estimated covariance matrices are slightly different except when the Logit link function is specified for binary response data.
Maximum number of iterations	specifies the maximum number of iterations to perform. If convergence is not attained in a specified number of iterations, the displayed output and all output data sets created by the task contain results that are based on the last maximum likelihood iteration.

Creating Output Data Sets

Option Name	Description
Output Data Sets
You can create two types of output data sets. Select the check box for each data set that you want to create. Create output data set outputs a data set that contains the specified statistics. Here are the statistics that you can include in the output data set: linear predictor predicted values confidence limits for predicted values Pearson residuals Deviance residuals Likelihood residuals standardized Pearson residuals standardized deviance residuals change in the chi-square goodness-of-fit from deleting the individual observation change in the deviance from deleting the individual observation leverage standardized DFBETA standard error of the linear predictor predicted probabilities for each response level Create scored data set outputs a data set that contains all the statistics in the output data set plus posterior probabilities.
Add SAS scoring code to the log	writes SAS DATA step code for computing predicted values of the fitted model either to a file or to a catalog entry. This code can then be included in a DATA step to score new data.