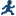Linear Regression Task

About the Linear Regression Task
Example: Predicting Weight Based on a Student’s Height
Assigning Data to Roles
Building a Model
Requirements for Building a Model
Create a Main Effect
Create Crossed Effects (Interactions)
Create a Nested Effect
Create a Full Factorial Model
Create N-Way Factorial
Create Polynomial Effects of the Nth Order
Setting the Model Options
Setting the Model Selection Options
Creating Output Data Sets

About the Linear Regression Task

The Linear regression task fits a linear model to predict a single continuous dependent variable from one or more continuous or categorical predictor variables. This task produces statistics and graphs for interpreting the results.
Note: You must have SAS/STAT to use this task.

Example: Predicting Weight Based on a Student’s Height

In this example, you want to use regression analysis to find out how well you can predict a child's weight if you know the child's height.
To create this example:
  1. In the Tasks section, expand the Statistics folder and double-click Linear Regression. The user interface for the Linear Regression task opens.
  2. On the Data tab, select the SASHELP.CLASS data set.
  3. Assign columns to these roles:
    Role
    Column Name
    Dependent variable
    Weight
    Classification variables
    Sex
    Continuous variables
    Age
    Height
  4. Click the Model tab and create these models:
    1. Select the Height variable, and then press Ctrl and select the Age variable. Click Add.
    2. Select the Height variable, and then press Ctrl and select the Sex variable. Click Cross.
    Creating Models for This Example in the Model Builder
  5. To run the task, click Submit SAS Code.
Here is a subset of the results:
Tabular Results for Linear Regression Example
Graph of the Observed Values by the Predicted Values for Weight
Fit Diagnostics for Weight in Linear Regression Example

Assigning Data to Roles

To run the Linear Regression task, you must assign a column to the Dependent variable role and a column to the Classification variables role or the Continuous variables role.
Role
Description
Roles
Dependent variable
specifies the numeric variable to use as the dependent variable for the regression analysis. You must assign a numeric variable to this role.
Classification variables
specifies categorical variables that enter the regression model through the design matrix coding.
Parameterization of Effects
Coding
specifies the parameterization method for the classification variable. Design matrix columns are created from the classification variables according to the selected coding scheme.
You can select from these coding schemes:
  • Effects coding specifies effect coding.
  • GLM coding specifies less-than-full-rank, reference-cell coding. This coding scheme is the default.
  • Reference coding specifies reference-cell coding.
Treatment of Missing Values
An observation is excluded from the analysis when either of these conditions is met:
  • if any variable in the model contains a missing value
  • if any classification variable contains a missing value (regardless of whether the classification variable is used in the model)
Continuous variables
specifies the numeric covariates (regressors) for the regression model.
Additional Roles
Frequency count
lists a numeric variable whose value represents the frequency of the observation. If you assign a variable to this role, the task assumes that each observation represents n observations, where n is the value of the frequency variable. If n is not an integer, SAS truncates it. If n is less than 1 or is missing, the observation is excluded from the analysis. The sum of the frequency variable represents the total number of observations.
Weight
specifies the variable to use as a weight to perform a weighted analysis of the data.
Group analysis by
specifies to create a separate analysis for each group of observations.

Building a Model

Requirements for Building a Model

To specify an effect, you must assign at least one column to the Classification variables role or the Continuous variables role. You can select combinations of variables to create crossed, nested, factorial, or polynomial effects. You can also specify whether to include the intercept in the model.
To create the model, use the model builder on the Model tab.

Create a Main Effect

  1. Select the variable name in the Variables box.
  2. Click Add to add the variable to the Model effects box.

Create Crossed Effects (Interactions)

  1. Select two or more variables in the Variables box. To select more than one variable, press Ctrl.
  2. Click Cross.

Create a Nested Effect

Nested effects are specified by following a main effect or crossed effect with a classification variable or list of classification variables enclosed in parentheses. The main effect or crossed effect is nested within the effects listed in parentheses. Here are examples of nested effects: B(A), C(B*A), D*E(C*B*A). In this example, B(A) is read "A nested within B."
  1. Select the effect name in the Model effects box.
  2. Click Nest. The Nested window opens.
  3. Select the variable to use in the nested effect. Click Outer or Nested within Outer to specify how to create the nested effect.
    Note: The Nested within Outer button is available only when a classification variable is selected.
  4. Click Add.

Create a Full Factorial Model

  1. Select two or more variables in the Variables box.
  2. Click Full Factorial.
For example, if you select the Height, Weight, and Age variables and then click Full Factorial, these model effects are created: Age, Height, Weight, Age*Height, Age*Weight, Height*Weight, and Age*Height*Weight.

Create N-Way Factorial

  1. Select two or more variables in the Variables box.
  2. Click N-way Factorial to add these effects to the Model effects box.
For example, if you select the Height, Weight, and Age variables and then specify the value of N as 2, when you click N-way Factorial, these model effects are created: Age, Height, Weight, Age*Height, Age*Weight, and Height*Weight. If N is set to a value greater than the number of variables in the model, N is effectively set to the number of variables.

Create Polynomial Effects of the Nth Order

  1. Select one variable in the Variables box.
  2. Specify higher-degree crossings by adjusting the number in the N field.
  3. Click Polynomial Order=N to add the polynomial effects to the Model effects box.
For example, if you select the Age and Height variables and then you specify 3 in the N field, when you click Polynomial Order=N, these model effects are created: Age, Age*Age, Age*Age*Age, Height, Height*Height, and Height*Height*Height.

Setting the Model Options

Option Name
Description
Methods
Confidence level
specifies the significance level to use for the construction of confidence intervals.
Statistics
You can choose to include the default statistics in the results or choose to include additional statistics.
Parameter Estimates
Standardized regression coefficients
displays the standardized regression coefficients. A standardized regression coefficient is computed by dividing a parameter estimate by the ratio of the sample standard deviation of the dependent variable to the sample standard deviation of the regressor.
Confidence limits for estimates
displays the 100 open 1 minus alpha close percent. Click image for alternative formats. upper and lower confidence limits for the parameter estimates.
Sums of Squares
Sequential sum of squares (Type I)
displays the sequential sums of squares (Type I SS) along with the parameter estimates for each term in the model.
Partial sum of squares (Type II)
displays the partial sums of squares (Type II SS) along with the parameter estimates for each term in the model.
Partial and Semipartial Correlations
Squared partial correlations
displays the squared partial correlation coefficients computed by using Type I and Type II sums of squares.
Squared semipartial correlations
displays the squared semipartial correlation coefficients computed by using Type I and Type II sums of squares. This value is calculated as sum of squares divided by the corrected total sum of squares.
Diagnostics
Analysis of influence
requests a detailed analysis of the influence of each observation on the estimates and the predicted values.
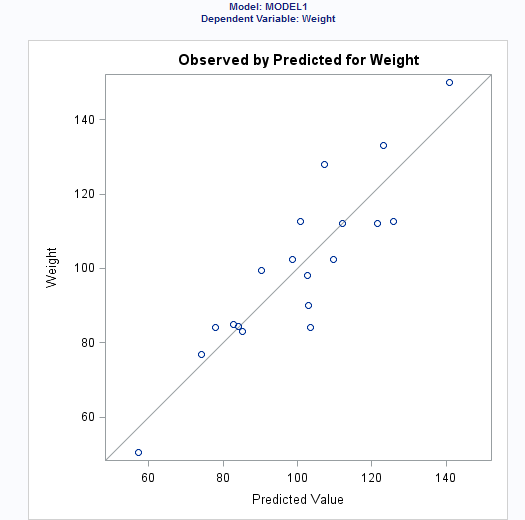
Analysis of residuals
requests an analysis of the residuals. The results include the predicted values from the input data and the estimated model, the standard errors of the mean predicted and residual values, the studentized residual, and Cook’s D statistic to measure the influence of each observation on the parameter estimates.
Predicted values
calculates predicted values from the input data and the estimated model.
Multiple Comparisons
Perform multiple comparisons
specifies whether to compute and compare the least squares means of fixed effects.
Select the effects to test
specifies the effects that you want to compare. You specified these effects on the Model tab.
Method
requests a multiple comparison adjustment for the p-values and confidence limits for the differences of the least squares means. Here are the valid methods: Bonferroni, Nelson, Scheffé, Sidak, and Tukey.
Significance level
requests that a t type confidence interval be constructed for each of the least squares means with a confidence level of 1 – number. The value of number must be between 0 and 1. The default value is 0.05.
Collinearity
Collinearity analysis
requests a detailed analysis of collinearity among the regressors. This includes eigenvalues, condition indices, and decomposition of the variances of the estimates with respect to each eigenvalue.
Tolerance values for estimates
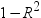produces tolerance values for the estimates. Tolerance for a variable is defined as 1 minus , r squared. Click image for alternative formats., where R square is obtained from the regression of the variable on all other regressors in the model.
Variance inflation factors
produces variance inflation factors with the parameter estimates. Variance inflation is the reciprocal of tolerance.
Heteroscedasticity
Heteroscedasticity analysis
performs a test to confirm that the first and second moments of the model are correctly specified.
Asymptotic covariance matrix
displays the estimated asymptotic covariance matrix of the estimates under the hypothesis of heteroscedasticity and heteroscedasticity-consistent standard errors of parameter estimates.
Plots
Diagnostic and Residual Plots
By default, several diagnostic plots are included in the results. You can also specify whether to include plots of the residuals for each explanatory variable.
More Diagnostic Plots
Rstudent statistic by predicted values
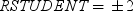plots studentized residuals by predicted values. If you select the Label extreme points option, observations with studentized residuals that lie outside the band between the reference lines r s t u d e n t equals plus minus 2. Click image for alternative formats. are deemed outliers.
DFFITS statistic by observations
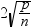plots the DFFITS statistic by observation number. If you select the Label extreme points option, observations with a DFFITS statistic greater in magnitude than 2 , square root of p over n end root. Click image for alternative formats. are deemed influential. The number of observations used is n, and the number of regressors is p.
DFBETAS statistic by observation number for each explanatory variable
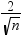produces panels of DFBETAS by observation number for the regressors in the model. You can view these plots as a panel or as individual plots. If you select the Label extreme points option, observations with a DFBETAS statistic greater in magnitude than fraction 2 , over square root of n end fraction. Click image for alternative formats. are deemed influential for that regressor. The number of observations used is n.
Label extreme points
identifies the extreme values on each different type of plot.
Scatter Plots
Fit plot for a single continuous variable
produces a scatter plot of the data overlaid with the regression line, confidence band, and prediction band for models with a single continuous variable. The intercept is excluded. When the number of points exceeds the value for the Maximum number of plot points option, a heat map is displayed instead of a scatter plot.
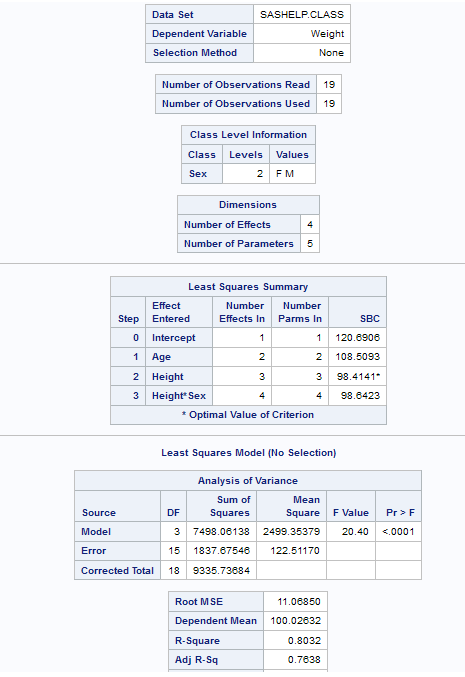
Observed values by predicted values
produces a scatter plot of the observed values versus the predicted values.
Partial regression plots for each explanatory variable
produces partial regression plots for each regressor. If you display these plots in a panel, there is a maximum of six regressors per panel.
Maximum number of plot points
specifies the maximum number of points to include in each plot.

Setting the Model Selection Options

Option
Description
Model Selection
Selection method
specifies the model selection method for the model. The task performs model selection by examining whether effects should be added to or removed from the model according to the rules that are defined by the selection method.
Here are the valid values for the selection methods:
  • None fits the full model.
  • Forward selection starts with no effects in the model and adds effects based on the value of the specified criterion.
  • Backward elimination starts with all the effects in the model and deletes effects based on the value of the specified criterion.
  • Stepwise selection is similar to the forward selection model. However, effects that are already in the model do not necessarily stay there. Effects are added to the model based on the values of the specified criteria.
Add/remove effects with
specifies the criterion to use to add or remove effects from the model.
Stop adding/removing effects with
specifies the criterion to use to stop adding or removing effects from the model.
Select best model by
specifies the criterion to use to identify the best fitting model.
Selection Statistics
Model fit statistics
specifies which model fit statistics are displayed in the fit summary table and the fit statistics tables. If you select Default fit statistics, the default set of statistics that are displayed in these tables includes all the criteria used in model selection.
Here are the additional fit statistics that you can include in the results:
  • Adjusted R-square
  • Akaike’s information criterion
  • Akaike’s information criterion corrected for small-sample bias
  • Mallows’ Cp
  • Press statistic, which specifies the predicted residual sum of squares statistic
  • R-square
  • Schwarz’s Bayesian information criterion
Selection Plots
Criteria plots
displays plots for these criteria: adjusted R-square, Akaike’s information criterion, Akaike’s information criterion corrected for small-sample bias, and the criterion used to select the best fitting model.
Coefficient plots
displays these plots:
  • a plot that shows the progression of the parameter values as the selection process proceeds
  • a plot that shows the progression of the criterion used to select the best fitting model
Details
Selection process details
specifies how much information about the selection process to include in the results. You can display a summary, details for each step of the selection process, or all of the information about the selection process.

Creating Output Data Sets

You can specify whether to create an observationwise statistics data set. This data set contains the sum of squares and cross-products.
You can also choose to include these statistics in the output data set:
  • predicted values
  • press statistic, which is the ith residual divided by 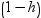open 1 minus h close. Click image for alternative formats., where h is the leverage, and where the model has been refit without the ith observation
  • residual
  • studentized residuals, which are the residuals divided by their standard errors
  • studentized residual with current observation removed
  • Cook’s D influence
  • the standard influence of observation on covariance of betas
  • the standard influence of an observation on predicted value (called DFFITS)
  • leverage
Copyright © SAS Institute Inc. All rights reserved.