The HPPLS Procedure

Partial Least Squares

Partial least squares (PLS) works by extracting one factor at a time. Let 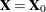$\mb{X}=\mb{X}_0$ be the centered and scaled matrix of predictors, and let 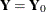$\mb{Y}=\mb{Y}_0$ be the centered and scaled matrix of response values. The PLS method starts with a linear combination 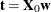$\mb{t} = \mb{X}_0\mb{w}$ of the predictors, where 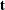$\mb{t}$ is called a score vector and 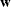$\mb{w}$ is its associated weight vector. 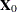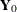The PLS method predicts both $\mb{X}_0$ and $\mb{Y}_0$ by regression on $\mb{t}$:

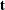\[ \begin{array}{rclcrcl} \hat{\mb{X}}_0 & = & \mb{t} \mb{p}’, & \textrm{where} & \mb{p}’ & = & (\mb{t}’\mb{t} )^{-1}\mb{t}’\mb{X}_0 \\ \hat{\mb{Y}}_0 & = & \mb{t} \mb{c}’, & \textrm{where} & \mb{c}’ & = & (\mb{t}’\mb{t} )^{-1}\mb{t}’\mb{Y}_0 \\ \end{array} \]

The vectors 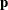$\mb{p}$ and $\mb{c}$ are called the X- and Y-loadings, respectively.

The specific linear combination 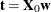$\mb{t} = \mb{X}_0\mb{w}$ is the one that has maximum covariance 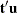$\mb{t}’\mb{u}$ with some response linear combination 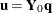$\mb{u} = \mb{Y}_0\mb{q}$. 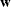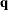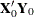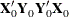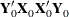Another characterization is that the X-weight, $\mb{w}$, and the Y-weight, $\mb{q}$, are proportional to the first left and right singular vectors, respectively, of the covariance matrix $\mb{X}_0’\mb{Y}_0$ or, equivalently, the first eigenvectors of $\mb{X}_0’\mb{Y}^{}_0\mb{Y}_0’\mb{X}^{}_0$ and $\mb{Y}_0’\mb{X}^{}_0\mb{X}_0’\mb{Y}^{}_0$, respectively.

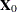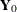This accounts for how the first PLS factor is extracted. The second factor is extracted in the same way by replacing $\mb{X}_0$ and $\mb{Y}_0$ with the X- and Y-residuals from the first factor:

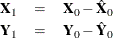
\begin{eqnarray*} \mb{X}_1 & = & \mb{X}_0 - \hat{\mb{X}}_0 \\ \mb{Y}_1 & = & \mb{Y}_0 - \hat{\mb{Y}}_0 \\ \end{eqnarray*}

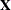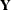These residuals are also called the deflated $\mb{X}$ and $\mb{Y}$ blocks. The process of extracting a score vector and deflating the data matrices is repeated for as many extracted factors as are wanted.