The FMM Procedure
Comparison with Roeder’s Method
It is important to note that Roeder’s original analysis proceeds in a different manner than the finite mixture modeling presented here. The technique presented by Roeder first develops a "best" range of scale parameters based on a specific criterion. Roeder then uses fixed scale parameters taken from this range to develop optimal equal-scale Gaussian mixture models.
You can reproduce Roeder’s point estimate for the density by specifying a five-component Gaussian mixture. In addition, use
the EQUATE=SCALE
option in the MODEL
statement and a RESTRICT
statement fixing the first component’s scale parameter at 0.9025 (Roeder’s h = 0.95, scale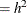 ). The combination of these options produces a mixture of five Gaussian components, each with variance 0.9025. The following
statements conduct this analysis:
). The combination of these options produces a mixture of five Gaussian components, each with variance 0.9025. The following
statements conduct this analysis:
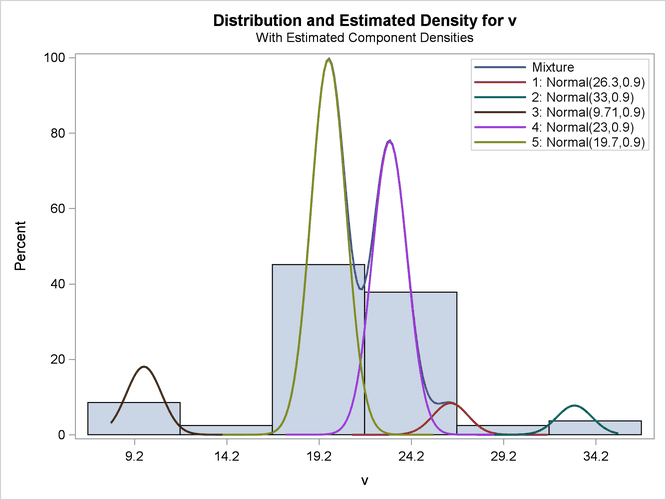
title2 "Five Components, Equal Variances = 0.9025"; proc fmm data=galaxies; model v = / K=5 equate=scale; restrict int 0 (scale 1) = 0.9025; run;
The output is shown in Figure 39.19 and Figure 39.20.
Figure 39.19: Reproduction of Roeder’s Five-Component Analysis of Galaxy Data
| Parameter Estimates for Normal Model | |||||
|---|---|---|---|---|---|
| Component | Parameter | Estimate | Standard Error |
z Value | Pr > |z| |
| 1 | Intercept | 26.3266 | 0.7778 | 33.85 | <.0001 |
| 2 | Intercept | 33.0443 | 0.5485 | 60.25 | <.0001 |
| 3 | Intercept | 9.7101 | 0.3591 | 27.04 | <.0001 |
| 4 | Intercept | 23.0295 | 0.2294 | 100.38 | <.0001 |
| 5 | Intercept | 19.7187 | 0.1784 | 110.55 | <.0001 |
| 1 | Variance | 0.9025 | 0 | ||
| 2 | Variance | 0.9025 | 0 | ||
| 3 | Variance | 0.9025 | 0 | ||
| 4 | Variance | 0.9025 | 0 | ||
| 5 | Variance | 0.9025 | 0 | ||
Figure 39.20: Density Plot for Roeder’s Analysis